Læringsmål
- At kende sammenhængen mellem syre- eller basestyrke og størrelsen af \(K_a\), \(K_b\), \(pK_a\) og \(pK_b\).
- For at forstå nivelleringseffekten.
Størrelsen af ligevægtskonstanten for en ioniseringsreaktion kan bruges til at bestemme den relative styrke af syrer og baser. For eksempel er den generelle ligning for ionisering af en svag syre i vand, hvor HA er modersyren og A- er dens konjugerede base, som følger:
\
Gligevægtskonstanten for denne dissociation er som følger:
\}{} \label{16.5.2}\]
Som vi bemærkede tidligere, er koncentrationen af vand stort set konstant for alle reaktioner i vandig opløsning, så \(\) i ligning \(\ref{16.5.2}\) kan indarbejdes i en ny størrelse, syreioniseringskonstanten (\(K_a\)), også kaldet syredissociationskonstanten:
\=\dfrac{}{}{} \label{16.5.3}\]
Sådan adskiller de numeriske værdier for K og \(K_a\) sig ved koncentrationen af vand (55,3 M). Igen kan \(H_3O^+\) for enkelhedens skyld skrives som \(H^+\) i ligning \(\ref{16.5.3}\). Husk dog på, at fri \(H^+\) ikke findes i vandige opløsninger, og at en proton overføres til \(H_2O\) i alle syreioniseringsreaktioner for at danne hydroniumioner, \(H_3O^+\). Jo større \(K_a\), jo stærkere er syren, og jo højere er \(H^+\)-koncentrationen ved ligevægt. Som alle andre ligevægtskonstanter måles syre-base-ioniseringskonstanterne faktisk i form af aktiviteterne af \(H^+\) eller \(OH^-\), hvilket gør dem enhedsløse. Værdierne af \(K_a\) for en række almindelige syrer er angivet i tabel \(\(\PageIndex{1}\).
svage baser reagerer med vand for at producere hydroxidionen, som vist i følgende generelle ligning, hvor B er moderbasen og BH+ er dens konjugerede syre:
\
Gligevægtskonstanten for denne reaktion er baseioniseringskonstanten (Kb), også kaldet basedissociationskonstanten:
\= \frac{}{} \label{16.5.5.5}\]
Egen gang er koncentrationen af vand konstant, så den optræder ikke i udtrykket for ligevægtskonstanten; i stedet er den medtaget i \(K_b\). Jo større \(K_b\), jo stærkere er basen og jo højere er \(OH^-\)-koncentrationen ved ligevægt. Værdierne af \(K_b\) for en række almindelige svage baser er angivet i tabel \(\PageIndex{2}\).
Der er en simpel sammenhæng mellem størrelsen af \(K_a\) for en syre og \(K_b\) for dens konjugerede base. Betragt f.eks. ioniseringen af cyanhydronsyre (\(HCN\)) i vand for at frembringe en sur opløsning og reaktionen af \(CN^-\) med vand for at frembringe en basisk opløsning:
\
\
Gligevægtskonstantudtrykket for ioniseringen af HCN er som følger:
\}{} \label{16.5.8}\]
Det tilsvarende udtryk for cyanidets reaktion med vand er som følger:
\}{} \label{16.5.9}\]
Hvis vi lægger ligningerne \(\ref{16.5.6}\) og \(\ref{16.5.7}\), får vi følgende:
| Reaktion | Ekvilibriumkonstanter |
|---|---|
| \(\cancel{HCN_{(aq)}} \rightleftharpoons H^+_{(aq)}+\cancel{CN^-_{(aq)}} \) | \(K_a=\cancel{}/\cancel{}\) |
| \(\cancel{CN^-_{(aq)}}+H_2O_{(l)} \rightleftharpoons OH^-_{(aq)}+\cancel{HCN_{(aq)}}}\) | \(K_b=\cancel{}/\cancel{}\) |
| \(H_2O_{(l)} \rightleftharpoons H^+_{(aq)}+OH^-_{(aq)}\) | \(K=K_a \times K_b=\) |
I dette tilfælde, er summen af de reaktioner, der beskrives af \(K_a\) og \(K_b\) ligningen for autoionisering af vand, og produktet af de to ligevægtskonstanter er \(K_w\):
\
Så hvis vi kender enten \(K_a\) for en syre eller \(K_b\) for dens konjugerede base, kan vi beregne den anden ligevægtskonstant for ethvert konjugeret syre-basepar.
Som med \(pH\), \(pOH\) og pKw kan vi bruge negative logaritmer for at undgå eksponentiel notation ved skrivning af syre- og baseioniseringskonstanter ved at definere \(pK_a\) på følgende måde:
\
\
og \(pK_b\) som
\
\
Sådan er ligningen \(\ref{16.5.10}\), som udtrykker forholdet mellem \(K_a\) og \(K_b\), kan skrives i logaritmisk form som følger:
\
Ved 25 °C bliver dette til
\
Værdierne for \(pK_a\) og \(pK_b\) er angivet for flere almindelige syrer og baser i tabellerne \(\PageIndex{1}\) og \(\PageIndex{2}\), og et mere omfattende datasæt findes i tabellerne E1 og E2. På grund af anvendelsen af negative logaritmer svarer mindre værdier af \(pK_a\) til større syreioniseringskonstanter og dermed til stærkere syrer. For eksempel er salpetersyre (\(HNO_2\)) med en \(pK_a\) på 3,25 ca. en million gange stærkere syre end cyanhydronsyre (HCN) med en \(pK_a\) på 9,21. Omvendt svarer mindre værdier af \(pK_b\) til større baseioniseringskonstanter og dermed til stærkere baser.
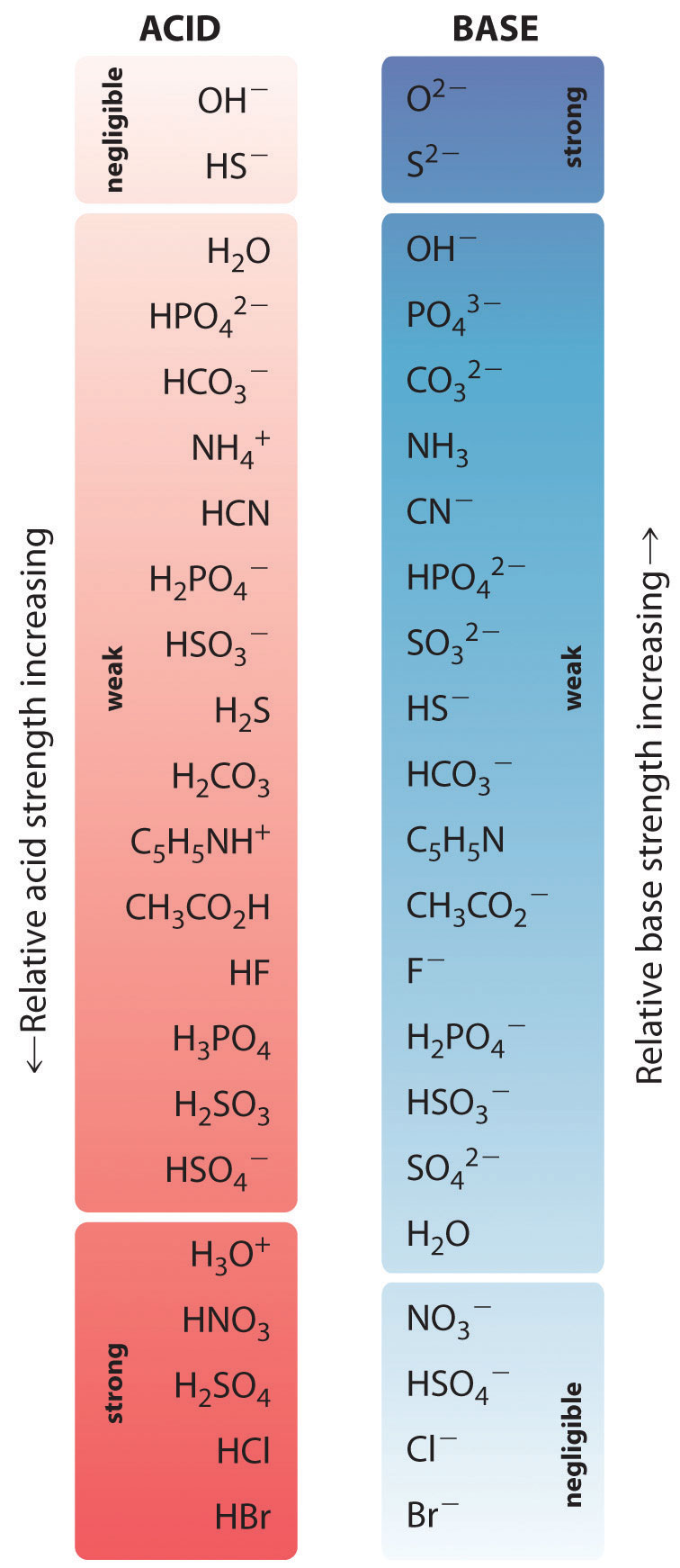
Den relative styrke af nogle almindelige syrer og deres konjugerede baser er vist grafisk i figur \(\PageIndex{1}\). De konjugerede syre-base-par er anført i rækkefølge (fra top til bund) efter stigende syrestyrke, hvilket svarer til faldende værdier af \(pK_a\). Denne rækkefølge svarer til faldende styrke af den konjugerede base eller stigende værdier af \(pK_b\). Nederst til venstre i figur \(\(\PageIndex{2}\) er de almindelige stærke syrer; øverst til højre er de mest almindelige stærke baser. Bemærk det omvendte forhold mellem styrken af den oprindelige syre og styrken af den konjugerede base. Således er den konjugerede base til en stærk syre en meget svag base, og den konjugerede base til en meget svag syre er en stærk base.
Den konjugerede base til en stærk syre er en svag base og omvendt.
Vi kan bruge de relative styrker af syrer og baser til at forudsige retningen af en syre-base-reaktion ved at følge en enkelt regel: En syre-base-ligevægt favoriserer altid den side med den svagere syre og base, som angivet med disse pile:
\
I en syre-base-reaktion reagerer protonerne altid med den stærkere base.
For eksempel er saltsyre en stærk syre, der ioniserer stort set fuldstændigt i fortyndet vandig opløsning for at danne \(H_3O^+\) og \(Cl^-\); kun ubetydelige mængder \(HCl\) molekyler forbliver udisocierede. Derfor ligger ioniseringsligevægten stort set helt til højre, som repræsenteret ved en enkelt pil:
I modsætning hertil er eddikesyre en svag syre, og vand er en svag base. Derfor indeholder vandige opløsninger af eddikesyre hovedsagelig eddikesyremolekyler i ligevægt med en lille koncentration af \(H_3O^+\) og acetationer, og ioniseringsligevægten ligger langt til venstre, som repræsenteret ved disse pile:
\
Sådan er det også tilfældet ved ammoniaks reaktion med vand, at hydroxidionen er en stærk base, og ammoniak er en svag base, mens ammoniumionen er en stærkere syre end vand. Derfor ligger denne ligevægt også til venstre:
\
Alle syre-base ligevægte favoriserer den side med den svagere syre og base. Protonerne er således bundet til den stærkere base.
Eksempel \(\PageIndex{1}\): Butyrat- og dimethylammoniumioner
- Beregne \(K_b\) og \(pK_b\) for butyrat-ionen (\(CH_3CH_2CH_2CO_2CO_2^-\)). \(pK_a\) for smørsyre ved 25°C er 4,83. Butyrsyre er ansvarlig for den fæle lugt af harsk smør.
- Beregn \(K_a\) og \(pK_a\) for dimethylammonium-ionen (\((CH_3)_2NH_2^+\)). Baseioniseringskonstanten \(K_b\) for dimethylamin (\((CH_3)_2NH\)) er \(5,4 \ gange 10^{-4}\) ved 25°C.
Givet: \(pK_a\) og \(K_b\)
Spørges om: tilsvarende \(K_b\) og \(pK_b\), \(K_a\) og \(pK_a\)
Strategi:
Konstanterne \(K_a\) og \(K_b\) er relateret som vist i ligning \(\(\ref{16.5.10}\). \(pK_a\) og \(pK_b\) for en syre og dens konjugerede base hænger sammen som vist i ligningerne \(\ref{16.5.15}\) og \(\(\ref{16.5.16}\). Brug relationerne pK = -log K og K = 10-pK (ligninger \(\ref{16.5.11}\) og \(\ref{16.5.13}\)) til at omregne mellem \(K_a\) og \(pK_a\) eller \(K_b\) og \(pK_b\).
Løsning:
Vi får \(pK_a\) for smørsyre og bliver bedt om at beregne \(K_b\) og \(pK_b\) for dens konjugerede base, butyrat-ionen. Da den angivne værdi for \(pK_a\) gælder for en temperatur på 25 °C, kan vi anvende ligning \(\ref{16.5.16}\): \(pK_a\) + \(pK_b\) = pKw = 14,00. Ved at erstatte \(pK_a\) og løse \(pK_b\),
Da \(pK_b = -\log K_b\), er \(K_b\) \(10^{-9,17} = 6,8 \ gange 10^{-10}\).
I dette tilfælde får vi \(K_b\) for en base (dimethylamin) og bliver bedt om at beregne \(K_a\) og \(pK_a\) for dens konjugerede syre, dimethylammoniumionen. Da den angivne begyndelsesmængde er \(K_b\) i stedet for \(pK_b\), kan vi bruge ligning \(\ref{16.5.10}\): \(K_aK_b = K_w\\). Ved at indsætte værdierne af \(K_b\) og \(K_w\) ved 25°C og løse for \(K_a\),
\
\
Da \(pK_a\) = -log \(K_a\), har vi \(pK_a = -\log(1,9 \ gange 10^{-11}) = 10,72\). Vi kunne også have omregnet \(K_b\) til \(pK_b\) for at få det samme svar:
Hvis vi får en af disse fire størrelser for en syre eller en base (\(K_a\), \(pK_a\), \(K_b\) eller \(pK_b\)), kan vi udregne de tre andre.
Ovelse \(\(\PageIndex{1}\)\): Mælkesyre
Mælkesyre (\(CH_3CH(OH)CO_2H\)) er ansvarlig for den skarpe smag og lugt af surmælk; man mener også, at den giver ømhed i trætte muskler. Dens \(pK_a\) er 3,86 ved 25°C. Beregn \(K_a\) for mælkesyre og \(pK_b\) og \(K_b\) for laktationen.
Svar
- \(K_a = 1,4 \ gange 10^{-4}\) for mælkesyre;
- \(pK_b\) = 10.14 og
- \(K_b = 7,2 \ gange 10^{-11}\) for laktat-ionen
- Solutions of Strong Acids and Bases: Du vil i tabel \(\(\PageIndex{1}\) bemærke, at syrer som \(H_2SO_4\) og \(HNO_3\) ligger over hydroniumionen, hvilket betyder, at de har \(pK_a\) værdier mindre end nul og er stærkere syrer end \(H_3O^+\) ionen. Husk fra kapitel 4, at den sure proton i stort set alle oxosyrer er bundet til et af oxygenatomerne i oxoanionen. Salpetersyre skal derfor korrekt skrives som \(HONO_2\). Desværre er formlerne for oxosyrer dog næsten altid skrevet med hydrogen til venstre og oxygen til højre, hvilket giver \(HNO_3\) i stedet. Faktisk har alle seks af de almindelige stærke syrer, som vi først stødte på i kapitel 4, \(pK_a\) værdier mindre end nul, hvilket betyder, at de har større tendens til at miste en proton end \(H_3O^+\) ionen. Omvendt er de konjugerede baser til disse stærke syrer svagere baser end vand. Derfor ligger protonoverførselsligevægtene for disse stærke syrer langt til højre, og tilsætning af en af de almindelige stærke syrer til vand resulterer i en stort set stoikiometrisk reaktion mellem syren og vand, hvorved der dannes en opløsning af \(H_3O^+\)-ionen og syrens konjugerede base.
- Polyprotiske syrer og baser
- Summary
- Nøgleligninger
- Medvirkende og bidragsydere
Solutions of Strong Acids and Bases: Du vil i tabel \(\(\PageIndex{1}\) bemærke, at syrer som \(H_2SO_4\) og \(HNO_3\) ligger over hydroniumionen, hvilket betyder, at de har \(pK_a\) værdier mindre end nul og er stærkere syrer end \(H_3O^+\) ionen. Husk fra kapitel 4, at den sure proton i stort set alle oxosyrer er bundet til et af oxygenatomerne i oxoanionen. Salpetersyre skal derfor korrekt skrives som \(HONO_2\). Desværre er formlerne for oxosyrer dog næsten altid skrevet med hydrogen til venstre og oxygen til højre, hvilket giver \(HNO_3\) i stedet. Faktisk har alle seks af de almindelige stærke syrer, som vi først stødte på i kapitel 4, \(pK_a\) værdier mindre end nul, hvilket betyder, at de har større tendens til at miste en proton end \(H_3O^+\) ionen. Omvendt er de konjugerede baser til disse stærke syrer svagere baser end vand. Derfor ligger protonoverførselsligevægtene for disse stærke syrer langt til højre, og tilsætning af en af de almindelige stærke syrer til vand resulterer i en stort set stoikiometrisk reaktion mellem syren og vand, hvorved der dannes en opløsning af \(H_3O^+\)-ionen og syrens konjugerede base.
Selv om \(K_a\) for \(HI\) er ca. 108 større end \(K_a\) for \(HNO_3\), giver reaktionen af enten \(HI\) eller \(HNO_3\) med vand en i det væsentlige stoikiometrisk opløsning af \(H_3O^+\) og I- eller \(NO_3^-\). Faktisk indeholder en 0,1 M vandig opløsning af en hvilken som helst stærk syre faktisk 0,1 M \(H_3O^+\), uanset hvilken stærk syre det drejer sig om. Dette fænomen kaldes udjævningseffekten: enhver art, der er en stærkere syre end vands konjugerede syre (\(H_3O^+\)), udjævnes til styrken af \(H_3O^+\) i vandig opløsning, fordi \(H_3O^+\) er den stærkeste syre, der kan eksistere i ligevægt med vand. Det er derfor umuligt at skelne mellem styrkerne af syrer som HI og HNO3 i vandig opløsning, og der må anvendes en alternativ metode til at bestemme deres relative syrestyrker.
En metode er at anvende et opløsningsmiddel som f.eks. vandfri eddikesyre. Da eddikesyre er en stærkere syre end vand, må den også være en svagere base, med en mindre tendens til at acceptere en proton end \(H_2O\). Målinger af ledningsevnen af 0,1 M opløsninger af både HI og \(HNO_3\) i eddikesyre viser, at HI er fuldstændig dissocieret, men \(HNO_3\) er kun delvist dissocieret og opfører sig som en svag syre i dette opløsningsmiddel. Dette resultat fortæller os klart, at HI er en stærkere syre end \(HNO_3\). Den relative rækkefølge af syrestyrker og de omtrentlige værdier for \(K_a\) og \(pK_a\) for de stærke syrer øverst i tabel \(\PageIndex{1}\) blev bestemt ved hjælp af målinger som denne og forskellige ikke-vandige opløsningsmidler.
I vandige opløsninger er \(H_3O^+\) den stærkeste syre, og \(OH^-\) er den stærkeste base, der kan eksistere i ligevægt med \(H_2O\).
Den nivellerende effekt gælder også for opløsninger af stærke baser: I vandig opløsning udjævnes enhver base, der er stærkere end OH-, til styrken af OH-, fordi OH- er den stærkeste base, der kan eksistere i ligevægt med vand. Salte som \(K_2O\), \(NaOCH_3\) (natriummethoxid) og \(NaNH_2\) (natriumamid eller natriumamid), hvis anioner er de konjugerede baser af arter, der ville ligge under vand i tabel \(\PageIndex{2}\), er alle stærke baser, der reagerer stort set fuldstændigt (og ofte voldsomt) med vand, idet de accepterer en proton og giver en opløsning af \(OH^-\) og det tilsvarende kation:
Andre eksempler, som du kan støde på, er kaliumhydrid (\(KH\)) og organometalliske forbindelser som f.eks. metyllithium (\(CH_3Li\)).
Polyprotiske syrer og baser
Som du har lært, indeholder polyprotiske syrer såsom \(H_2SO_4\), \(H_3PO_4\) og \(H_2CO_3\) mere end én ioniserbar proton, og protonerne går tabt trinvis. Den fuldt protonerede art er altid den stærkeste syre, fordi det er lettere at fjerne en proton fra et neutralt molekyle end fra en negativt ladet ion. Syrestyrken aftager således med tabet af efterfølgende protoner, og tilsvarende stiger \(pK_a\). Tag for eksempel \(H_2SO_4\):
\
Ligevægten i den første reaktion ligger langt til højre, hvilket er i overensstemmelse med, at \(H_2SO_4\) er en stærk syre. I den anden reaktion er der derimod betydelige mængder af både \(HSO_4^-\) og \(SO_4^{2-}\) til stede ved ligevægt.
For en polyprotisk syre falder syrestyrken, og \(pK_a\) stiger med det sekventielle tab af hver enkelt proton.
Ved hydrogen sulfat ionen (\(HSO_4^-\)) er både den konjugerede base af \(H_2SO_4\) og den konjugerede syre af \(SO_4^{2-}\). Ligesom vand kan HSO4- derfor fungere som enten syre eller base, alt efter om den anden reaktant er en stærkere syre eller en stærkere base. Omvendt er sulfat-ionen (\(SO_4^{2-}\)) en polyprotisk base, der er i stand til at acceptere to protoner trinvis:
\
\
Som ethvert andet konjugeret syre-basepar hænger styrkerne af de konjugerede syrer og baser sammen ved \(pK_a\) + \(pK_b\) = pKw. Tag f.eks. det konjugerede syre-basepar \(HSO_4^-/ SO_4^{2-}\). Af tabel \(\(\PageIndex{1}\) fremgår det, at \(pK_a\) for \(HSO_4^-\) er 1,99. Derfor er \(pK_b\) for \(SO_4^{2-}\) \(SO_4^{2-}\) 14,00 – 1,99 = 12,01. Sulfat er således en ret svag base, mens \(OH^-\) er en stærk base, så den i ligning \(\ref{16.6}\) viste ligevægt ligger til venstre. \(HSO_4^-\)-ionen er også en meget svag base (\(pK_a\) for \(H_2SO_4\) = 2,0, \(pK_b\) for \(HSO_4^- = 14 – (-2,0) = 16\)), hvilket er i overensstemmelse med, hvad vi forventer for den konjugerede base til en stærk syre.
Eksempel \(\PageIndex{2}\)
Forudsig, om ligevægten for hver reaktion ligger til venstre eller til højre som skrevet.
- \(NH^+_{4(aq)}+PO^{3-}_{4(aq)} \rightleftharpoons NH_{3(aq)}+HPO^{2−}_{4(aq)}\)
- \(CH_3CH_2CO_2H_{(aq)}+CN^−_{(aq)} \rightleftharpoons CH_3CH_2CO^-_{2(aq)}+HCN_{(aq)}\)
Givet: balanceret kemisk ligning
Spørges om: ligevægtsposition
Strategi:
Identificer de konjugerede syre-basepar i hver reaktion. Henvis derefter til tabellerne \(\PageIndex{1}\)og\(\PageIndex{2}\) og figur \(\PageIndex{2}\) for at bestemme, hvilken syre og base der er den stærkeste. Ligevægt favoriserer altid dannelsen af det svageste syre-basepar.
Løsning:
De konjugerede syre-basepar er \(NH_4^{4+/NH_3\) og \(HPO_4^{2-}/PO_4^{3-}\). I henhold til tabellerne \(\(\PageIndex{1}\) og \(\(\PageIndex{2}\) er \(NH_4^+\) en stærkere syre (\(pK_a = 9.25\)) end \(HPO_4^{2-}\) (pKa = 12,32), og \(PO_4^{3-}\) er en stærkere base (\(pK_b = 1,68\)) end \(NH_3\) (\(pK_b = 4,75\)). Ligevægten vil derfor ligge til højre og begunstige dannelsen af det svagere syre-basepar:
\
De konjugerede syre-basepar er \(CH_3CH_2CO_2H/CH_3CH_2CO_2CO_2^-\) og \(HCN/CN^-\). I henhold til tabel \(\PageIndex{1}\) er HCN en svag syre (pKa = 9,21) og \(CN^-\) en moderat svag base (pKb = 4,79). Propionsyre (\(CH_3CH_2CO_2CO_2H\)) er dog ikke opført i tabel \(\PageIndex{1}\). I en situation som denne er den bedste fremgangsmåde at lede efter en lignende forbindelse, hvis syre-base-egenskaber er opført. F.eks. er propionsyre og eddikesyre identiske bortset fra de grupper, der er knyttet til carbonatomet i carboxylsyren (\(\ce{-CH_2CH_3}\) versus \(\ce{-CH_3}\))), så vi kan forvente, at de to forbindelser har lignende syre-base-egenskaber. Især ville vi forvente, at \(pK_a\) for propionsyre ville være af samme størrelsesorden som \(pK_a\) for eddikesyre. (Faktisk er \(pK_a\) for propionsyre 4,87, sammenlignet med 4,76 for eddikesyre, hvilket gør propionsyre til en lidt svagere syre end eddikesyre). Propionsyre burde således være en betydeligt stærkere syre end \(HCN\). Da den stærkere syre danner den svagere konjugerede base, forudsiger vi, at cyanid vil være en stærkere base end propionat. Ligevægten vil derfor ligge til højre og favorisere dannelsen af det svagere syre-basepar:
\
Øvelse \(\PageIndex{1}\)
Forudsig, om ligevægten for hver reaktion ligger til venstre eller til højre som skrevet.
- \(H_2O_{(l)}+HS^-_{(aq)} \rightleftharpoons OH^−_{(aq)}+H_2S_{(aq)}\)
- \(HCO^−_{2(aq)}+HSO^−_{4(aq)} \rightleftharpoons HCO_2H_{(aq)}+SO^{2-}_{4(aq)}\)
Svar a
venstre
Svar b
venstre
Summary
Syre-base-reaktioner indeholder altid to konjugerede syre-base-par. Hver syre og hver base har en tilknyttet ioniseringskonstant, der svarer til dens syre- eller basestyrke. To arter, der kun adskiller sig med en proton, udgør et konjugeret syre-basepar. Størrelsen af ligevægtskonstanten for en ioniseringsreaktion kan bruges til at bestemme den relative styrke af syrer og baser. For en vandig opløsning af en svag syre kaldes dissociationskonstanten for syreioniseringskonstanten (\(K_a\)). På samme måde er ligevægtskonstanten for en svag bases reaktion med vand ioniseringskonstanten for baser (\(K_b\)). For ethvert konjugeret syre-basepar er \(K_aK_b = K_w\). Mindre værdier af \(pK_a\) svarer til større syreioniseringskonstanter og dermed til stærkere syrer. Omvendt svarer mindre værdier af \(pK_b\) til større ioniseringskonstanter for baser og dermed til stærkere baser. Ved 25 °C er \(pK_a + pK_b = 14,00\). Syre-base-reaktioner forløber altid i den retning, der giver det svageste syre-base-par. Der kan ikke findes nogen syre stærkere end \(H_3O^+\) og ingen base stærkere end \(OH^-\) i vandig opløsning, hvilket fører til det fænomen, der er kendt som nivelleringseffekten. Polyprotiske syrer (og baser) mister (og får) protoner trinvis, idet den fuldt protonerede art er den stærkeste syre og den fuldt deprotonerede art er den stærkeste base.
Nøgleligninger
- Syreioniseringskonstant: \=\dfrac{}{}{} \]
- Baseioniseringskonstant: \= \dfrac{}{}{} \]
- Sammenhæng mellem \(K_a\) og \(K_b\) for et konjugeret syre-basepar: \
- Definition af \(pK_a\\): \ \
- Definition af \(pK_b\): \ \
- Definition af \(pK_b\): \ \ \
- Sammenhæng mellem \(pK_a\) og \(pK_b\) for et konjugeret syre-basepar: \ \ \
Medvirkende og bidragsydere
-
Stephen Lower, professor emeritus (Simon Fraser U.) Chem1 Virtual Textbook