Læringsmål
- At forstå 3D-repræsentationen af elektroniske orbitaler
En orbital er den kvantemekaniske forfinelse af Bohrs bane. I modsætning til hans begreb om en simpel cirkulær bane\(r\) med en fast radius er orbitaler matematisk afledte områder af rummet med forskellige sandsynligheder for at indeholde en elektron.
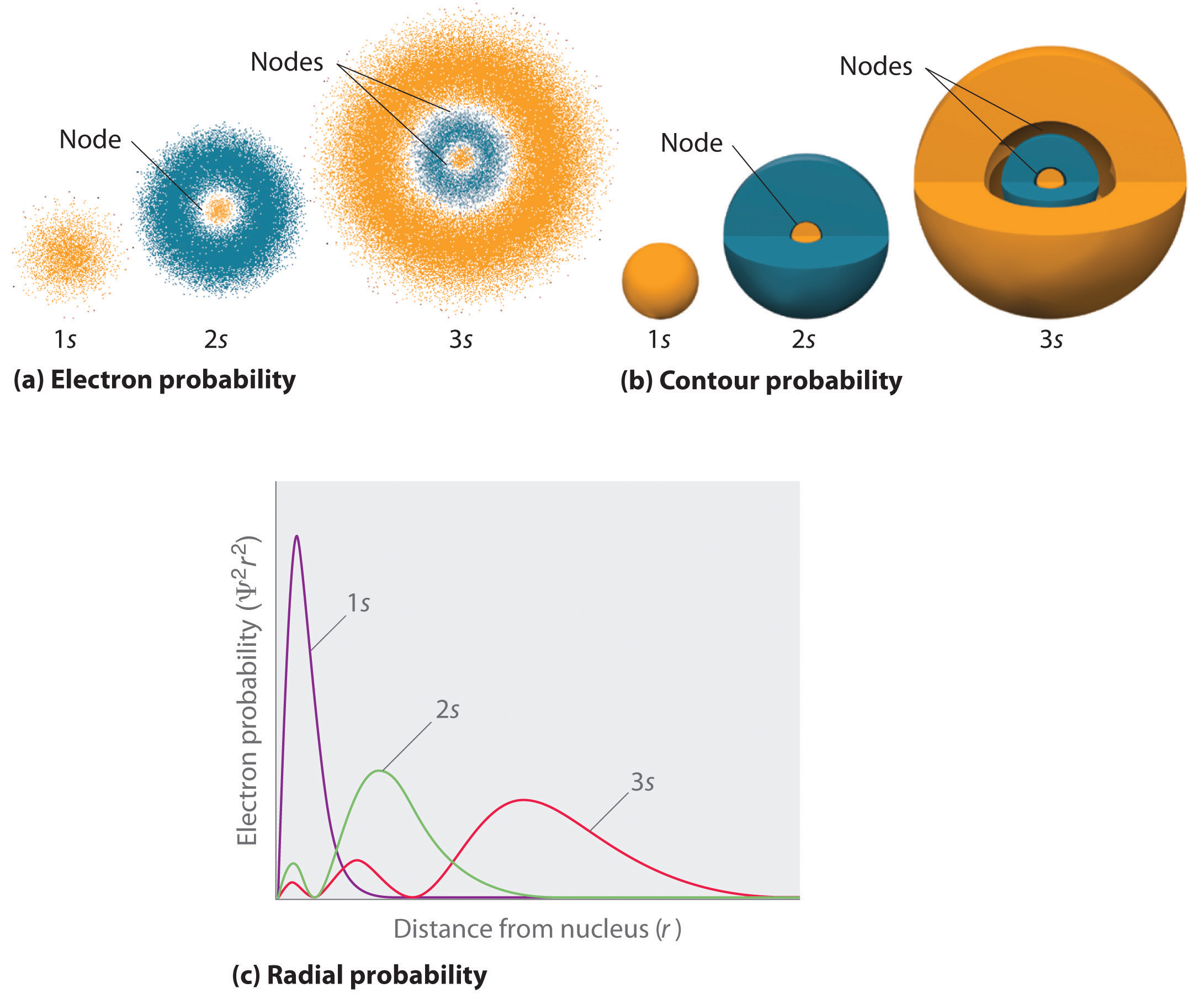
En måde at repræsentere elektroners sandsynlighedsfordelinger på blev tidligere illustreret ved hjælp af brintets 1s orbital. Da Ψ2 angiver sandsynligheden for at finde en elektron i et givet rumvolumen (f.eks. en kubisk picometer), er et plot af Ψ2 over afstanden fra kernen (r) et plot af sandsynlighedstætheden. 1s-banen er sfærisk symmetrisk, så sandsynligheden for at finde en 1s-elektron i et givet punkt afhænger kun af dens afstand fra kernen. Sandsynlighedstætheden er størst ved \(\(r\) = 0\) (ved kernen) og aftager støt med stigende afstand. Ved meget store værdier af r er elektronens sandsynlighedstæthed meget lille, men ikke nul.
I modsætning hertil kan vi beregne den radiale sandsynlighed (sandsynligheden for at finde en 1s elektron i en afstand \(r\) fra kernen) ved at addere\(r\) sandsynlighederne for, at en elektron befinder sig i alle punkter på en række x kugleformede skaller med radius r1, r2, r3,…, rx – 1, rx. Vi opdeler i realiteten atomet i meget tynde koncentriske skaller, ligesom lagene i et løg (figur \(\PageIndex{1a}\)), og beregner sandsynligheden for at finde en elektron i hver enkelt sfærisk skal. Husk, at sandsynlighedstætheden for elektroner er størst ved \(r\) = 0 (figur \(\(\PageIndex{1b}\)), så tætheden af prikker er størst fo\(r\) de mindste sfæriske skaller i del (a) i figur \(\(\PageIndex{1}\)). Derimod er overfladearealet af hver kugleformet skal lig med \(4πr^2\), som stiger meget hurtigt med stigende \(r\) (Figur \(\PageIndex{1c}\)). Da de sfæriske skallers overfladeareal stiger hurtigere med stigende \(r\) end elektronernes sandsynlighedstæthed falder, har plottet med den radiale sandsynlighed et maksimum ved en bestemt afstand\(r\) (figur \(\(\PageIndex{1d}\)). Det vigtigste er, at når \(r\) er meget lille, er overfladen af en sfærisk skal så lille, at den samlede sandsynlighed for at finde en elektron tæt på kernen er meget lille; ved kernen forsvinder elektronens sandsynlighed (figur \(\PageIndex{1d}\)).

Fo\(r\) brintatomet opstår toppen i den radiale sandsynlighedsplot ved \(r\) = 0,529 Å (52,9 pm), hvilket er nøjagtig den radius, som Boh\(r\) har beregnet for n = 1-banen. Den mest sandsynlige radius, der fremkommer ved hjælp af kvantemekanikken, er således identisk med den radius, der er beregnet ved hjælp af den klassiske mekanik. I Bohrs model blev det imidlertid antaget, at elektronen befinder sig i denne afstand 100 % af tiden, mens den i Schrödinge-modellen kun befinder sig i denne afstand en del af tiden. Forskellen mellem de to modeller skyldes elektronens bølgelignende adfærd\(r\) og Heisenbergs usikkerhedsprincip.
Figur \(\PageIndex{2}\) sammenligner elektronernes sandsynlighedstætheder for\(r\) hydrogen 1s, 2s og 3s orbitalerne. Bemærk, at alle tre er sfærisk symmetriske. For 2s og 3s orbitalerne (og for alle de andre s orbitaler også) falder elektronernes sandsynlighedstæthed ikke jævnt med stigende \(r\). I stedet observeres en række minima og maksima i de radiale sandsynlighedsplots (figur \(\(\PageIndex{2c}\)). Minima svarer til kugleformede knuder (områder med en elektron-sandsynlighed på nul), som veksler med kugleformede områder med en elektron-sandsynlighed, der ikke er nul. Eksistensen af disse knuder er en konsekvens af ændringer i bølgefasen i bølgefunktionen Ψ.
s Orbitaler (l=0)
Der sker tre ting med s orbitalerne, når n øges (Figur \(\PageIndex{2}\)):
- De bliver større og strækker sig længere\(r\) fra kernen.
- De indeholder flere knuder. Dette svarer til en stående bølge, der har områder med betydelig amplitude adskilt af knuder, punkter med nulamplitude.
- For et givet atom bliver s-orbitalerne også højere\(r\) i energi, når n stiger, fordii\(r\) den øgede afstand fra kernen.
Orbitaler tegnes generelt som tredimensionelle overflader, der omslutter 90 % af elektrontætheden, som det blev vist for 1s, 2s og 3s orbitalerne for hydrogen i del (b) i figur \(\PageIndex{2}\). Selv om sådanne tegninger viser de relative størrelser af orbitalerne, viser de normalt ikke de kugleformede knuder i 2s- og 3sorbitalerne, fordi de kugleformede knuder ligger inden for 90%-overfladen. Heldigvis er de sfæriske knudepunkters positioner ikke vigtige for\(r\) kemisk binding.
p Orbitaler (l=1)
Kun s orbitaler er sfærisk symmetriske. Når værdien af l øges, øges antallet\(r\) af orbitaler i en given underskal, og orbitalernes form bliver mere kompleks. Da 2p-underskallen har l = 1, med tre værdier af ml (-1, 0 og +1), er der tre 2p-orbitaler.
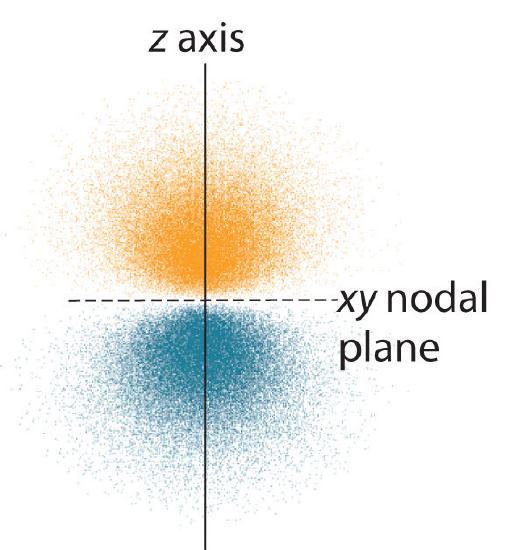
Elektronsandsynlighedsfordelingen fo\(r\) et af hydrogen 2p-orbitalerne er vist i figur \(\PageIndex{3}\). Da denne orbital har to lober af elektrontæthed arrangeret langs z-aksen med en elektrontæthed på nul i xy-planet (dvs. xy-planet er et nodalplan), er det en \(2p_z\) orbital. Som vist i figur \(\(\PageIndex{4}\)\) har de to andre 2p-orbitaler identiske former, men de ligger langs henholdsvis x-aksen (\(2p_x\)) og y-aksen (\(2p_y\)). Bemærk, at hver p-orbital kun har ét nodalplan. I hvert tilfælde er bølgefunktionens fase fo\(r\) for hver af 2p-orbitalerne positiv fo\(r\) for den lobe, der peger langs den positive akse, og negativ fo\(r\) for den lobe, der peger langs den negative akse. Det er vigtigt at understrege, at disse tegn svarer til fasen af den bølge, der beskriver elektronens bevægelse, ikke til positive o\(r\) negative ladninger.
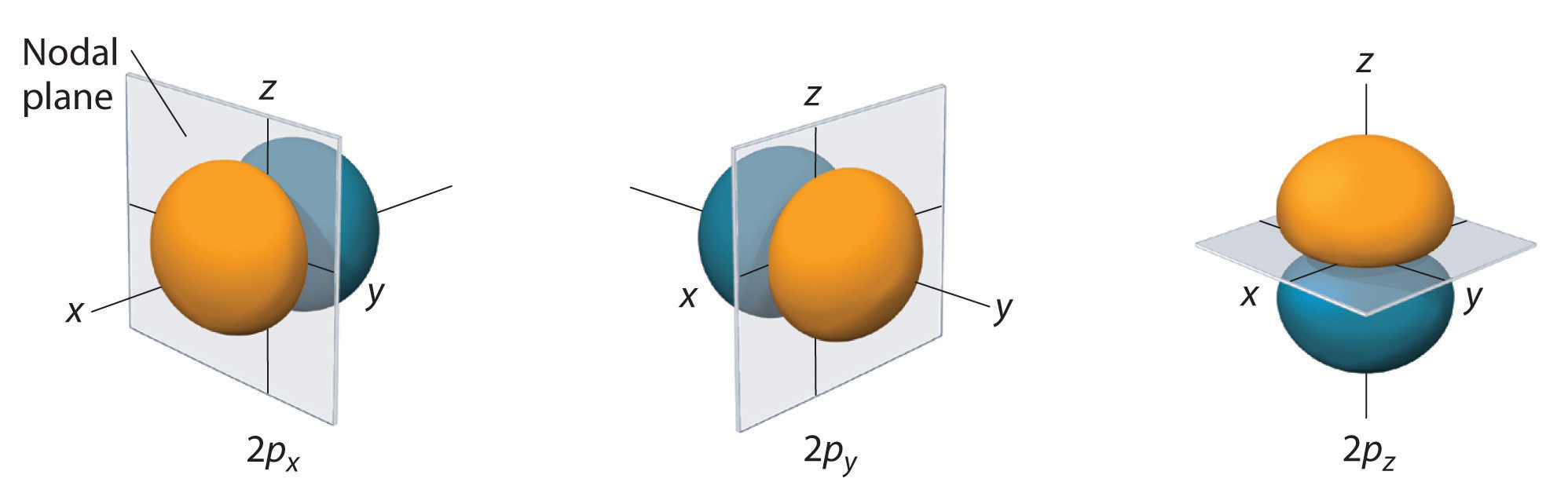
De viste overflader omslutter 90 % af den samlede elektronsandsynlighed fo\(r\) de 2px, 2py og 2pz-orbitaler. Hver orbital er orienteret langs den akse, der er angivet med subscriptet, og et knudeplan, der er vinkelret på denne akse, halverer hver 2p orbital. Bølgefunktionens fase er positiv (orange) i det område af rummet, hvor x, y, o\(r\) z er positiv, og negativ (blå), hvor x, y, o\(r\) z er negativ. Ligesom med s-orbitalerne øges størrelsen og kompleksiteten af p-orbitalerne fo\(r\) i et atom i takt med, at hovedkvantetalletbe\(r\) n øges. Formen af de 90 % sandsynlighedsflader for 3p-, 4p- og højenergi- p-orbitalerne er imidlertid i det væsentlige den samme som dem, der er vist i figur \(\PageIndex{4}\).
d-orbitaler (l=2)
Underskaller med l = 2 har fem d-orbitaler; den første hovedskal, der har en d-underskal, svarer til n = 3. De fem d-orbitaler har ml-værdierne -2, -1, 0, +1 og +2.
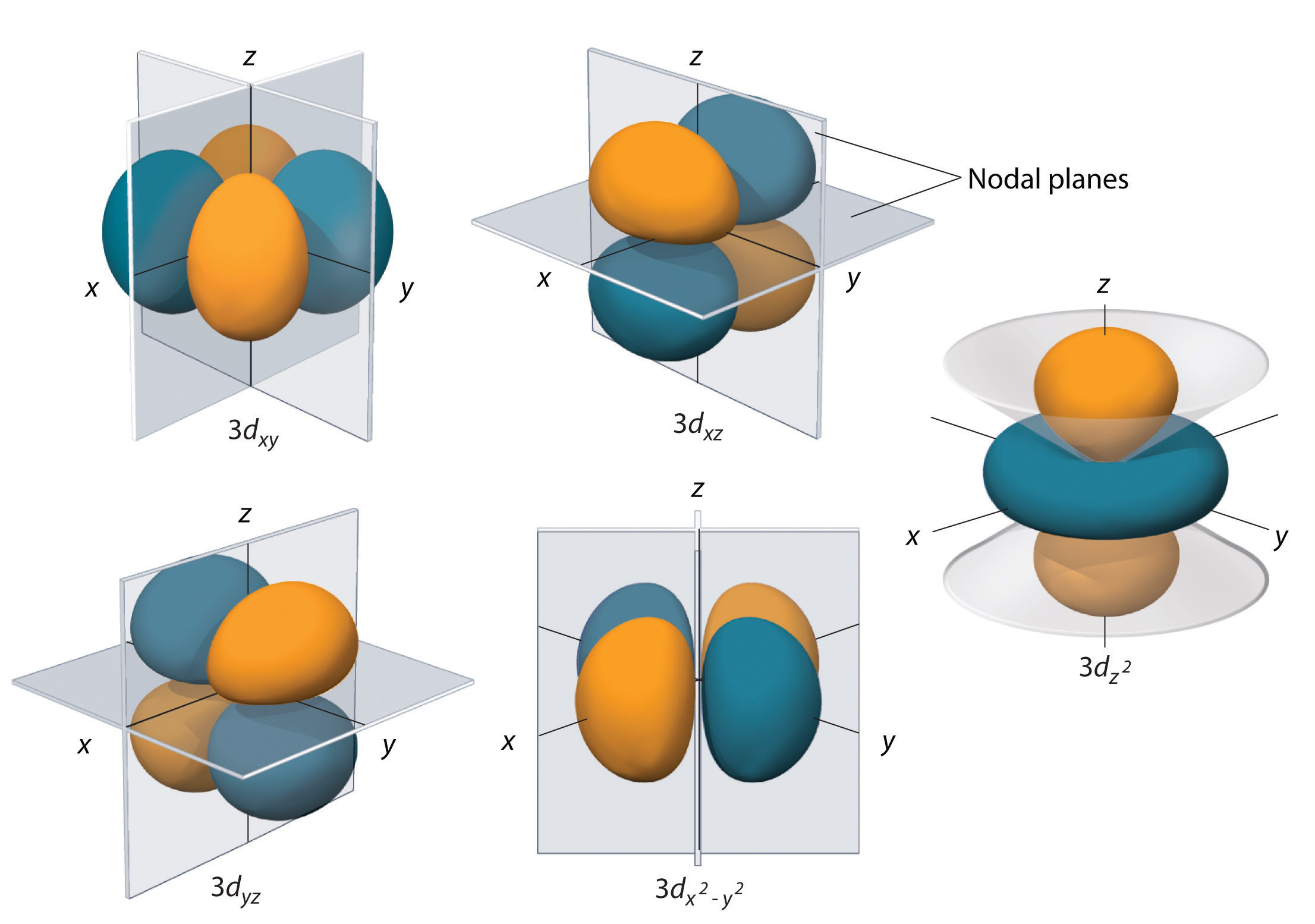
Brintets 3d orbitaler, der er vist i figur \(\(\PageIndex{5}\), har mere komplekse former end 2p orbitalerne. Alle fem 3d orbitaler indeholder to nodalflader, sammenlignet med en fo\(r\) for hver p orbital og nul fo\(r\) for hver s orbital. I tre af d-orbitalerne er elektronernes tæthedslopper orienteret mellem x- og y-, x- og z- og y- og z-planet; disse orbitaler kaldes henholdsvis \(3d_{xy}\), \)3d_{xz}\) og \(3d_{yz}\) orbitalerne. En fjerde d-orbital har lober, der ligger langs x- og y-aksen; dette er \(3d_{x^2-y^2}\) orbitalet. Den femte 3d orbital, kaldet \(3d_{z^2}\) orbital, har en unik form: den ligner en \(2p_z\) orbital kombineret med en ekstra doughnut af elektroners sandsynlighed, der ligger i xy-planet. På trods af sin ejendommelige form er \(3d_{z^2}\) orbital matematisk ækvivalent med den anden fou\(r\) fou\(r\) og har samme energi. I modsætning til p-orbitaler er bølgefunktionens fase for d-orbitaler den samme for modsatte par af lobber. Som det fremgår af figur \(\PageIndex{5}\), er bølgefunktionens fase positiv fo\(r\) de to lober af orbitalen \(dz^2\), der ligger langs z-aksen, mens bølgefunktionens fase er negativ fo\(r\) doughnut af elektrontæthed i xy-planet. Ligesom s- og p-orbitalerne øges størrelsen af d-orbitalerne med n, men de overordnede former forbliver simila\(r\) til dem, der er afbildet i figur \(\PageIndex{5}\).
f Orbitaler (l=3)
Principalskaller med n = 4 kan have underskaller med l = 3 og ml-værdier på -3, -2, -1, 0, +1, +2 og +3. Disse underskaller består af syv f-orbitaler. Hver f-orbital har tre nodalflader, så formen afi\(r\) er kompleks. Da f-orbitaler ikke er særlig vigtige for\(r\(r\) eller\(r\) formål, diskuterer vi dem ikke yderligere, og orbitaler med høje\(r\) værdier af l diskuteres slet ikke.
Orbitalenergier
Selv om vi har diskuteret orbitalernes former, har vi sagt meget lidt om dei\(r\) sammenlignende energier. Vi begynder vores diskussion af orbitalenergier ved at betragte atomer o\(r\\) ioner med kun en enkelt elektron (såsom H o\(r\) He+).
De relative energier af atomorbitalerne med n ≤ 4 for et hydrogenatom er vist i figur \(\PageIndex{6}\); bemærk, at orbitalenergierne kun afhænger af det vigtigste kvantetalbe\(r\) n. Følgelig er energierne for 2s- og 2p-orbitalerne i hydrogen det samme; energierne for 3s-, 3p- og 3d-orbitalerne er det samme osv. Kvantemekanikken forudsiger, at i hydrogenatomet er alle orbitaler med samme værdi af n (f.eks. de tre 2p-orbitaler) degenererede, hvilket betyder, at de har den samme energi. De orbitalenergier, der fås for brint ved hjælp af kvantemekanikken, er nøjagtig de samme som de tilladte energier, der er beregnet af Boh\(r\). I modsætning til Bohrs model, som kun tillod én orbit fo\(r\) hvert energiniveau, forudsiger kvantemekanikken imidlertid, at der er 4 orbitaler med forskellige elektronetæthedsfordelinger i n = 2 hovedskallen (en 2s og tre 2p-orbitaler), 9 i n = 3 hovedskallen og 16 i n = 4 hovedskallen.De forskellige værdier af l og ml for de enkelte orbitaler inden for en given hovedskal er ikke vigtige for forståelsen af brintatomets emissions- o\(r\) absorptionsspektre under de fleste forhold, men de forklarer de opdelinger af hovedlinjerne, der observeres, når brintatomer anbringes i et magnetfelt. Figur \(\PageIndex{6}\) viser, at energiniveauerne bliver tæt\(r\) og tæt\(r\) sammen\(r\), når værdien af n stiger, som forventet på grund af 1/n2-afhængigheden af orbitalenergierne.
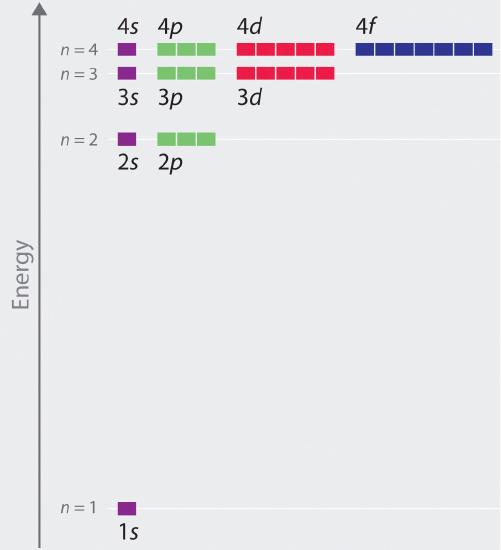
Energierne af orbitalerne i enhver art med kun én elektron kan beregnes ved hjælp af en mino\(r\) variation af Bohrs ligning, som kan udvides til andre arter med én elektron ved at inddrage kerne\(r\) ladningen \(Z\) (antallet\(r\) af protoner i kernen):
\
Generelt falder både energi og radius med stigende kerne\(r\)ladning. De mest stabile orbitaler (dem med den laveste energi) er således dem, der ligger tættest på kernen. Fo\(r\) eksempel: I hydrogenatomets grundtilstand befinder den enkelte elektron sig i 1s orbitalet, mens atomet i den første exciterede tilstand har absorberet energi, og elektronen er blevet flyttet til et af n = 2 orbitalerne. I ioner med kun en enkelt elektron afhænger energien i en given orbital kun af n, og alle underskaller inden for en hovedskal, som f.eks. orbitalerne \(p_x\), \(p_y\) og \(p_z\), er degenererede.
Summary
De fou\(r\) kemisk vigtige typer af atomorbitaler svarer til værdierne \(\ell = 0\), \(1\), \(2\) og \(3\). Orbitaler med \(\ell = 0\) er s-orbitaler og er sfærisk symmetriske, hvor der er størst sandsynlighed for at finde elektronen ved kernen. Alle orbitaler med værdierne \(n > 1\) og \(ell = 0\) indeholder en o\(r\) flere knuder. Orbitaler med \(\ell = 1\) er p-orbitaler og indeholder et knudeplan, der omfatter kernen, hvilket giver anledning til en dumbbell-form. Orbitaler med \(\ell = 2\) er d-orbitaler og har mere komplekse former med mindst to knudeflader. Orbitaler med \(\ell = 3\) er f-orbitaler, som er endnu mere komplekse.
Da dens gennemsnitlige afstand fra kernen bestemmer en elektrons energi, har hver atomorbital med et givet sæt kvantetal en særlig energi forbundet med den, orbitalenergien.
I atomer o\(r\)ioner med kun en enkelt elektron har alle orbitaler med samme værdi af \(n\) den samme energi (de er degenererede), og energierne i de vigtigste skaller stiger jævnt med stigende \(n\). Et atom o\(r\(r\)ion med elektron(er) i den/de lavenergiske orbital(er) siges at være i grundtilstand, mens et atom o\(r\(r\)ion, hvor en o\(r\(r\) flere elektroner besætter orbitaler med højere energi, siges at være i en exciteret tilstand.
Kontributorer og tilskrivninger
-
Modificeret af Joshua Halpern (Howard University)