En asymptote er en linje, som en graf nærmer sig, men som den ikke skærer.
I denne lektion lærer vi at finde lodrette asymptoter, vandrette asymptoter og skrå (skrå) asymptoter for rationelle funktioner.
Relaterede emner:
Flere lektioner om regning

Det følgende diagram viser de forskellige typer af asymptoter: vandrette asymptoter, lodrette asymptoter og skrå asymptoter. Rul ned ad siden for at få flere eksempler og løsninger på, hvordan man finder asymptoter.

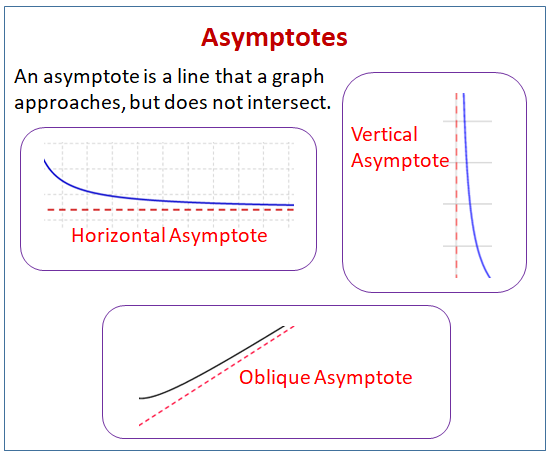
Hvordan bestemmer man den lodrette asymptot?

Metode 1: Brug definitionen af lodret asymptot

Linjen x = a kaldes en lodret asymptot til kurven y = f(x), hvis mindst et af følgende udsagn er sandt.

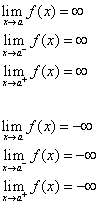
Metode 2:

For rationelle funktioner er lodrette asymptoter lodrette linjer, der svarer til nulpunkterne i nævneren.
Givet den rationelle funktion, f(x)

Strin 1: Skriv f(x) i reduceret form

Strin 2: Hvis x – c er en faktor i nævneren, så er x = c den lodrette asymptote.

Eksempel:

Find de lodrette asymptoter for

Løsning:

Metode 1: Brug definitionen af lodret asymptote.

Hvis x er tæt på 3, men større end 3, så er nævneren x – 3 et lille positivt tal, og 2x er tæt på 8. Så er et stort positivt tal.

Intuitivt ser vi, at

Sådan er det også, hvis x ligger tæt på 3, men er mindre end 3, så er x – 3 et lille negativt tal, og 2x er tæt på 8. Så er et stort negativt tal.

Linjen x = 3 er den lodrette asymptote.

Metode 2:

Stræk 1: f(x) er allerede i reduceret form.

Stræk 2: Nævneren er x – 3, og derfor er den lodrette asymptote ved x = 3.

Find lodrette asymptoter af rationelle funktioner

Hvad man skal kigge efter, for at finde lodrette asymptoter af rationelle funktioner.

• Vis trinvise løsninger

Vertikale asymptoter af rationelle funktioner: Hurtig måde at finde dem på

Eksempel på at finde lodrette asymptoter for rationelle funktioner.

• Vis trinvise løsninger

Sådan finder man lodrette asymptoter for rationelle funktioner

• Vis trinvise løsninger

Hvordan bestemmer man den vandrette asymptote?

Metode 1: Brug definitionen af horisontal asymptote

Linjen y = L kaldes en horisontal asymptote til kurven y = f(x), hvis enten

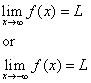
Metode 2:

For den rationelle funktion, f(x)

Hvis graden af x i tælleren er mindre end graden af x i nævneren, så er y = 0 den vandrette asymptot.

Hvis graden af x i tælleren er lig med graden af x i nævneren, så er y = c, hvor c fås ved at dividere de ledende koefficienter.

Eksempel:

Find de vandrette og lodrette asymptoter for funktionen.

Løsning:

Metode 1:

Divider både tæller og nævner med x.

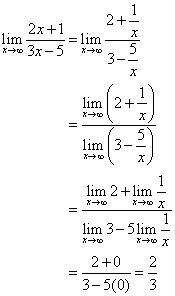
Linjen er den vandrette asymptote.

Metode 2:

Graden af x i tælleren er lig med graden af x i nævneren.

Dividerer vi de ledende koefficienter får vi

Linjen er den vandrette asymptote.

Kortvej til at finde horisontale asymptoter af rationelle funktioner

Et par tricks, der gør det meget nemt at finde horisontale asymptoter af rationelle funktioner

• Vis trin-for-trin-løsninger

Denne video vil give et grundlæggende overblik over horisontale asymptoter. Vi vil afgøre, om de givne rationelle funktioner har horisontale asymptoter, og hvad de er.

• Vis trinvise løsninger

Denne video vil gå yderligere i detaljer om reglerne for horisontale asymptoter.

• Vis trinvise løsninger

Oblik asymptote eller skrå asymptote

Nogle kurver har asymptoter, der er skrå, det vil sige hverken horisontale eller vertikale.

Hvis så kaldes linjen y = mx + b for skrå eller skrå asymptote, fordi de lodrette afstande mellem kurven y = f(x) og linjen y = mx + b nærmer sig 0.

For rationale funktioner opstår skrå asymptoter, når tællerens grad er én mere end nævnerens grad. I et sådant tilfælde kan ligningen for den skråtstillede asymptote findes ved lang division.

Eksempel:

Find asymptoterne for funktionen

Løsning:

Da nævneren x2 + 1 aldrig er 0, er der ingen lodret asymptote.

Da graden af x i tælleren er større end graden af x i nævneren, er der ingen vandret asymptote.

Da graden af x i tælleren er én større end graden af x i nævneren, kan vi bruge lang division til at opnå den skrå asymptote.

Linjen y = x er altså den skrå asymptote.

Finding af skrå asymptoter for rationelle funktioner

Denne video beskriver, hvornår en rationel funktion har en skrå asymptote, beskriver kort, hvad en skrå asymptote er, og laver derefter to eksempler.

• Vis trin-for-trin-løsninger

Find asymptoter af en rationel funktion (lodret, vandret og skrå/skrå)

Denne video viser, hvordan man finder de lodrette asymptoter og en skrå/skrå asymptote af en rationel funktion.

• Vis trin-for-trin-løsninger

Find alle asymptoter af en rationel funktion (lodret, vandret, skråt/skråt)

Her ser vi på en funktion og finder den lodrette asymptote og konkluderer også, at der ikke findes nogen vandrette asymptoter, men at der findes en skrå asymptote. Vi bruger derefter lang division til at finde den skrå asymptote.

• Vis trinvise løsninger

Prøv den gratis Mathway-regnemaskine og problemløser nedenfor for at øve dig i forskellige matematiske emner. Prøv de givne eksempler, eller indtast dit eget problem, og tjek dit svar med trin-for-trin-forklaringerne.