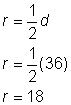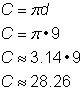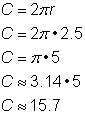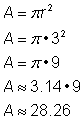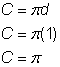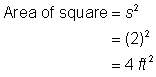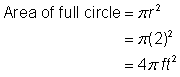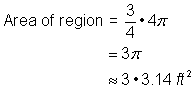Cirkler
Læringsmål)
– Identificere egenskaber ved cirkler.
– Finde omkredsen af en cirkel.
– Finde arealet af en cirkel.
– Finde arealet og omkredsen af sammensatte geometriske figurer.
Introduktion
Cirkler er en almindelig form. Man ser dem overalt – hjul på en bil, frisbees, der flyver gennem luften, compactdiske, der leverer data. Det er alle sammen cirkler.
En cirkel er en todimensionel figur ligesom polygoner og firkantede figurer. Cirkler måles dog anderledes end disse andre figurer – man er endda nødt til at bruge nogle forskellige udtryk for at beskrive dem. Lad os tage et kig på denne interessante form.
Cirkels egenskaber
En cirkel repræsenterer et sæt punkter, som alle er lige langt væk fra et fast, centralt punkt. Dette faste punkt kaldes centrum. Afstanden fra cirklens centrum til et hvilket som helst punkt på cirklen kaldes radius.
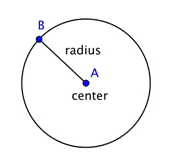
Når to radier (pluralis af radius) sættes sammen til et linjestykke på tværs af cirklen, har man en diameter. Diameteren af en cirkel går gennem cirklens centrum og har sine endepunkter på selve cirklen.
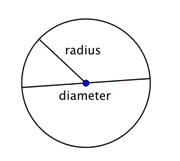
Diameteren af en hvilken som helst cirkel er to gange længden af denne cirkels radius. Den kan repræsenteres ved udtrykket 2r, eller “to gange radius”. Så hvis du kender en cirkels radius, kan du gange den med 2 for at finde diameteren; det betyder også, at hvis du kender en cirkels diameter, kan du dividere med 2 for at finde radius.
|
Eksempel |
||
|
Problem |
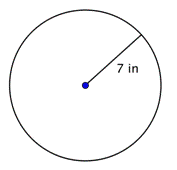
Find cirklens diameter.
|
|
|
d = 2r d = 2(7) d = 14 |
Diameteren er to gange radius, eller 2r. Radius i denne cirkel er 7 tommer, så diameteren er 2(7) = 14 tommer. |
|
|
Svar |
Diameteren er 14 tommer. |
|
|
Eksempel |
||
|
Problem |
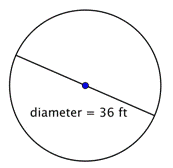
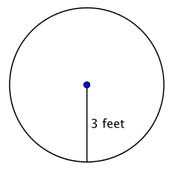
Find cirklens radius.
|
|
|
|
Radius er det halve af diameteren, eller |
|
|
Svar |
Radius er 18 fod. |
|
Cirkelomkreds
Afstanden rundt om en cirkel kaldes omkredsen. (Husk, at afstanden rundt om en polygon er omkredsen.)
En interessant egenskab ved cirkler er, at forholdet mellem en cirkels omkreds og dens diameter er det samme for alle cirkler. Uanset cirklens størrelse vil forholdet mellem omkreds og diameter være det samme.
Nedenfor er der angivet nogle faktiske mål for forskellige genstande. Målingerne er nøjagtige til nærmeste millimeter eller kvart tomme (afhængigt af den anvendte måleenhed). Se på forholdet mellem omkredsen og diameteren for hver enkelt genstand – selv om genstandene er forskellige, er forholdet for hver enkelt omtrent det samme.
|
Post |
Omkreds (C) (afrundet til nærmeste hundrededel) |
Diameter (d) |
Forhold |
|
Kop |
253 mm |
79 mm |
|
|
Kvarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
Omkredsen og diameteren er omtrentlige mål, da der ikke er nogen præcis måde at måle disse dimensioner nøjagtigt på. Hvis man kunne måle dem mere præcist, ville man imidlertid opdage, at forholdet ![]() ville bevæge sig i retning af 3,14 for hver af de angivne størrelser. Det matematiske navn for forholdet
ville bevæge sig i retning af 3,14 for hver af de angivne størrelser. Det matematiske navn for forholdet ![]() er pi, og det repræsenteres af det græske bogstav
er pi, og det repræsenteres af det græske bogstav ![]() .
.
![]() er et decimaltal uden afslutning og uden gentagelse, så det er umuligt at skrive det fuldstændigt ud. De første 10 cifre i
er et decimaltal uden afslutning og uden gentagelse, så det er umuligt at skrive det fuldstændigt ud. De første 10 cifre i ![]() er 3,141592653; det bliver ofte afrundet til 3,14 eller anslået som brøken
er 3,141592653; det bliver ofte afrundet til 3,14 eller anslået som brøken ![]() . Bemærk, at både 3,14 og
. Bemærk, at både 3,14 og ![]() er tilnærmelser af
er tilnærmelser af![]() og bruges i beregninger, hvor det ikke er vigtigt at være præcis.
og bruges i beregninger, hvor det ikke er vigtigt at være præcis.
Da du ved, at forholdet mellem omkreds og diameter (eller ![]() ) er ensartet for alle cirkler, kan du bruge dette tal til at finde omkredsen af en cirkel, hvis du kender dens diameter.
) er ensartet for alle cirkler, kan du bruge dette tal til at finde omkredsen af en cirkel, hvis du kender dens diameter.
![]() =
= ![]() , så C =
, så C = ![]() d
d
Og da d = 2r, så er C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Cirkelomkreds
For at finde omkredsen (C) af en cirkel skal du bruge en af følgende formler:
Hvis du kender diameteren (d) af en cirkel: ![]()
Hvis du kender cirklens radius (r): ![]()
Hvis du kender cirklens radius (r): ![]()
|
Eksempel |
||
|
Problem |
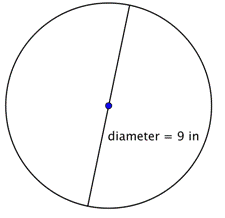
Find omkredsen af cirklen.
|
|
|
|
For at beregne omkredsen, givet en diameter på 9 tommer, skal du bruge formlen Da du bruger en tilnærmelse for |
|
|
Svar |
Omkredsen er 9 |
|
|
Eksempel |
||
|
Problem |
Find omkredsen af en cirkel med en radius på 2.5 yards. |
|
|
|
For at beregne omkredsen af en cirkel givet en radius på 2,5 yards skal du bruge formlen |
|
|
Svar |
Omkredsen er 5 |
|
En cirkel har en radius på 8 tommer. Hvad er dens omkreds, afrundet til nærmeste tomme?
A) 25 tommer
B) 50 tommer
C) 64 tommer2
D) 201 tommer
Area
![]() er et vigtigt tal i geometri. Du har allerede brugt det til at beregne omkredsen af en cirkel. Du bruger
er et vigtigt tal i geometri. Du har allerede brugt det til at beregne omkredsen af en cirkel. Du bruger ![]() også, når du skal regne arealet af en cirkel ud.
også, når du skal regne arealet af en cirkel ud.
Aarealet af en cirkel
For at finde arealet (A) af en cirkel skal du bruge formlen: ![]()
|
Eksempel |
||
|
Problem |
Find arealet af cirklen.
|
|
|
|
For at finde arealet af denne cirkel skal du bruge formlen Husk at skrive svaret i kvadratiske enheder, da du finder arealet. |
|
|
Svar |
Aarealet er 9 |
|
En knap har en diameter på 20 millimeter. Hvad er knappens areal? Brug 3,14 som en tilnærmelse af ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Sammensatte figurer
Nu, hvor du ved, hvordan du beregner omkredsen og arealet af en cirkel, kan du bruge denne viden til at finde omkredsen og arealet af sammensatte figurer. Tricket til at finde ud af disse typer problemer er at identificere figurer (og dele af figurer) i den sammensatte figur, beregne deres individuelle dimensioner og derefter lægge dem sammen.
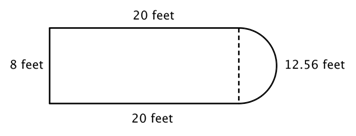
Se f.eks. på billedet nedenfor. Er det muligt at finde omkredsen?
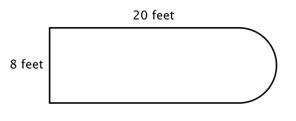
Det første skridt er at identificere enklere figurer inden for denne sammensatte figur. Du kan opdele den i et rektangel og en halvcirkel, som vist nedenfor.
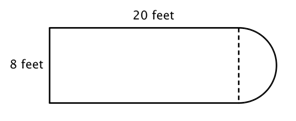
Du ved, hvordan du kan finde omkredsen af et rektangel, og du ved, hvordan du kan finde omkredsen af en cirkel. Her er omkredsen af de tre faste sider af rektanglet 8 + 20 + 20 = 48 fod. (Bemærk, at kun tre sider af rektanglet vil indgå i omkredsen af den sammensatte figur, fordi den anden side ikke ligger ved en kant; den er dækket af halvcirklen!)
For at finde omkredsen af halvcirklen skal du bruge formlen ![]() med en diameter på 8 fod, og derefter tage halvdelen af resultatet. Omkredsen af halvcirklen er
med en diameter på 8 fod, og derefter tage halvdelen af resultatet. Omkredsen af halvcirklen er ![]() , eller ca. 12,56 fod, så den samlede omkreds er ca. 60,56 fod.
, eller ca. 12,56 fod, så den samlede omkreds er ca. 60,56 fod.
|
Eksempel |
||
|
Problem |
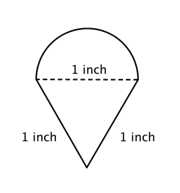
Find omkredsen (til nærmeste hundrededel) af den sammensatte figur, der består af en halvcirkel og en trekant.
|
|
|
|
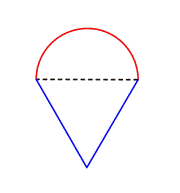
Identificer mindre figurer inden for den sammensatte figur. Denne figur indeholder en halvcirkel og en trekant. |
|
|
Diameter (d) = 1
Halvcirklens omkreds = |
Find omkredsen af cirklen. Divider derefter med 2 for at finde halvcirklens omkreds. |
|
|
|
|
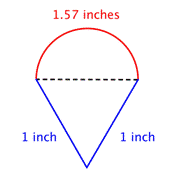
Find den samlede omkreds ved at lægge halvcirklens omkreds og længderne af de to ben sammen. Da vores måling af halvcirklens omkreds er tilnærmelsesvis, vil omkredsen også være en tilnærmelse. |
|
Svar |
Omkring 3.57 tommer |
|
|
Eksempel |
||
|
Problem |
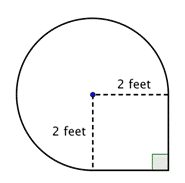
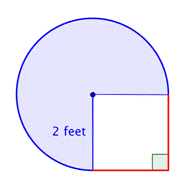
Find arealet af den sammensatte figur, der består af tre fjerdedele af en cirkel og et kvadrat, med en nøjagtighed på nærmeste hundrededel.
|
|
|
|
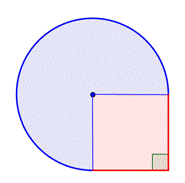
Identificer mindre figurer inden for den sammensatte figur. Denne figur indeholder et cirkulært område og et kvadrat. Hvis du finder arealet af hver af dem, kan du finde arealet af hele figuren. |
|
|
|
Find arealet af kvadratet. |
|
|
|
|
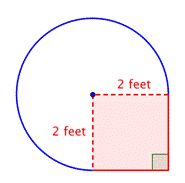
Find arealet af det cirkulære område. Radius er 2 fod. Opmærksomheden henledes på, at området er |
|
|
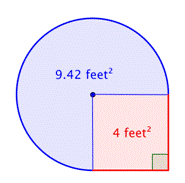
4 fod2 + |
Sæt de to områder sammen. Da din måling af cirklens areal er en tilnærmelse, vil figurens areal også være en tilnærmelse. |
|
Svar |
Overfladen er ca. 13.42 fod2. |
|
Hvad er arealet (til nærmeste hundrededel) af den nedenfor viste figur? (Begge de afrundede områder er halvcirkler.)
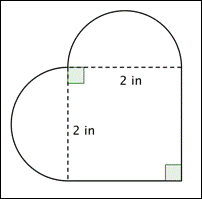
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3.14 in2
Summarum
Cirkler er en vigtig geometrisk form. Afstanden rundt om en cirkel kaldes omkredsen, og det indre rum i en cirkel kaldes arealet. Beregning af omkredsen og arealet af en cirkel kræver et tal kaldet pi (![]() ), som er et ikke afsluttende, ikke gentagende decimaltal. Pi tilnærmes ofte ved hjælp af værdierne 3,14 og
), som er et ikke afsluttende, ikke gentagende decimaltal. Pi tilnærmes ofte ved hjælp af værdierne 3,14 og ![]() . Du kan finde omkredsen eller arealet af sammensatte figurer – herunder figurer, der indeholder cirkulære dele – ved at anvende omkreds- og arealformlerne, hvor det er relevant.
. Du kan finde omkredsen eller arealet af sammensatte figurer – herunder figurer, der indeholder cirkulære dele – ved at anvende omkreds- og arealformlerne, hvor det er relevant.