Det følgende er mit bud på nogle matematiske problemer i formodet “common core-matematik” eller “ny matematik”, som har cirkuleret på internettet. Jeg mener, at de viser os en forkert implementering af CCS.
Hold dig for øje, at ikke alt, hvad du ser i matematikbøger eller på internettet, er korrekt udført på baggrund af CCS. I nogle af de eksempler, du ser, ser det ud til, at folk smider den sunde fornuft ud, når de laver matematikopgaver for at imødekomme Common Core-standarderne!
Jeg er ikke overrasket over, at implementeringen er endt med at blive “forkludret” nogle steder. CCS er en sådan ændring for de fleste lærere, at de har brug for masser af støtte og omskoling, før de skal undervise efter dem.
Jeg har altid ment, at det VIGTIGSTE problem, som matematikundervisningen i folkeskolens grundskoler står over for, er, at mange folkeskolelærere ikke forstår matematik tilstrækkeligt til at kunne undervise rigtigt i den, selv på folkeskoleniveau. Mange af dem forstår f.eks. ikke begreberne, hvorfor og hvorledes de algoritmer, de underviser i, fungerer. Det er ikke deres skyld – problemet kan spores tilbage til det, de blev undervist i på læreruddannelsen og i deres egen skolegang.
Selv selve standarddokumentet er nogle steder noget svært at følge. At læse det kræver en del eftertanke. Jeg ville ønske, at nogen ville lave et hæfte, der forklarer standarderne i et enkelt sprog og med mange eksempler.
Dårlige eksempler på “common core” eller “ny matematik”
Eksempel 1
For nylig så jeg et billede af subtraktionsstrategier på Facebook, som påstod, at det var fra en matematikbog for 1. klasse og var “Common Core-matematik”.”
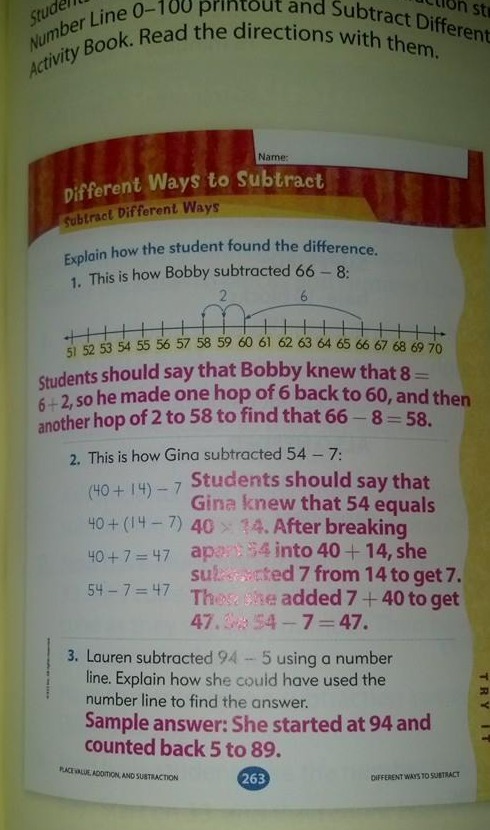
Jeg synes, at metode 2 er alt for svær til 1. klasse, og jeg ville endda lade metode 1 være til 2. klasse.
Den bog ser dog ikke engang ud til at være i overensstemmelse med Common Core-standarderne. Standarderne for 1. klasse omfatter simpelthen ikke den slags subtraktionsproblemer!
Dette er, hvad vi finder i standarderne:
Tilføj og subtraherer inden for 20.
1.OA.5
Relaterer tælling til addition og subtraktion (f.eks. ved at tælle på 2 for at lægge 2 til 2).
1.OA.6.
Addér og subtraherer inden for 20, idet du demonstrerer færdighed i addition og subtraktion inden for 10. Bruge strategier som at tælle videre; lave ti (f.eks. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); nedbryde et tal, der fører til et ti-tal (f.eks. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); bruge forholdet mellem addition og subtraktion (f.eks. ved at vide, at 8 + 4 = 12, ved man, at 12 – 8= 4); og skabe tilsvarende, men lettere eller kendte summer (f.eks, addere 6 + 7 ved at skabe den kendte ækvivalente 6 + 6 + 1 = 12 + 1 = 13).
Lærebogens eksempel synes at ville tage fat på 1.OA.6 ovenfor, men det er tydeligvis for addition og subtraktion inden for 20, ikke med større tal.
Sidst i standarderne for 1. klasse ser vi to standarder, der har at gøre med subtraktion af tocifrede tal (inden for 100):
1.NBT.5.
Givet et tocifret tal skal du mentalt finde 10 mere eller 10 mindre end tallet uden at skulle tælle; du skal forklare den anvendte begrundelse.
1.NBT.6.
Subtrahere multipla af 10 i intervallet 10-90 fra multipla af 10 i intervallet 10-90 (positive eller nulforskelle) ved hjælp af konkrete modeller eller tegninger og strategier baseret på stedværdi, operationernes egenskaber og/eller forholdet mellem addition og subtraktion; relatere strategien til en skriftlig metode og forklare den anvendte begrundelse.
Marias note: Dette betyder subtraktioner såsom 34 – 20 eller 89 – 60.
men ingen af disse omfatter subtraktioner som f.eks. 54 – 7 eller 82 – 6. Disse er i 2. klasse:
2.NBT.5
Addonerer og subtraherer flydende inden for 100 ved hjælp af strategier, der er baseret på stedværdi, operationernes egenskaber og/eller forholdet mellem addition og subtraktion.
Bemærk, at standarden for 2. klasse ikke angiver, HVORDAN man subtraherer (om man bruger strategier for mentalt regnearbejde eller skriver tal under hinanden og låner/regrupperer).
Eksempel 2
Fra Houghton Mifflin, angiveligt:
Juanita ønsker at give poser med klistermærker til sine venner. Hun ønsker at give det samme antal klistermærker til hver veninde. Hun er ikke sikker på, om hun skal bruge 4 poser eller 6 poser med klistermærker. Hvor mange klistermærker kan hun købe, så der ikke er nogen klistermærker tilbage?
Stikmærkeproblemet har at gøre med begrebet det mindste fælles multiplum (LCM). (Svaret er, at hun skal købe 12, 24, 36 eller et hvilket som helst andet multiplum af 12 klistermærker, for så kan hun dele dem enten i 4 poser eller 6 poser.)
Sikkert, problemet er MEGET uklart og dårligt formuleret. Mit gæt er, at det hæfte, som dette står i, simpelthen er uredigeret. Det er ikke selve normerne selv skyld i det. Jeg er enig med Bart Goddard på Matematikforum. Dette er et symptom på det blinde hastværk med at producere “virkelighedsnære” historieproblemer, som ender med at være meningsløse.
Fra PDF-dokumentet, som det optræder i, konkluderer jeg, at opgaven er for fjerde klasse, fordi alle de andre ordproblemer i hæftet svarer til standarderne for fjerde klasse (faktorer, primtal). Men CCS inkluderer ikke engang det mindst almindelige multiplum i standarderne for 4. klasse (det er i 6.)!!! Der er virkelig gået noget galt med den ordopgave.
Eksempel 3
Agennemgang, angiveligt fra Houghton Mifflin for 1. klasse. Det svarer til den standard, som jeg allerede har citeret ovenfor:
Adderer og subtraherer inden for 20.
1.OA.6.
Adderer og subtraherer inden for 20, idet man demonstrerer flydende addition og subtraktion inden for 10. Bruge strategier som at tælle videre; lave ti (f.eks. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); nedbryde et tal, der fører til et ti-tal (f.eks. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); bruge forholdet mellem addition og subtraktion (f.eks, ved at vide, at 8 + 4 = 12, ved man, at 12 – 8 = 4); og skabe ækvivalente, men lettere eller kendte summer (f.eks. addere 6 + 7 ved at skabe den kendte ækvivalent 6 + 6 + 1 = 12 + 1 = 13).
Nu har strategien med at “lave ti” først og fremmest noget at gøre med ADDITION, ikke subtraktion. Ved subtraktion kaldes det at “nedbryde et tal, der fører til en ti”. Så instruktionerne burde sige: “Hvilken viser en måde at dekomponere et tal, der fører til en tier?” Jeg mener, at det er fuldstændig NONSENSE at kræve, at elever i 1. klasse skal kende denne terminologi.
Men der er et andet problem her. Hvis du rent faktisk læser alle standarderne, vil du bemærke, at der flere andre steder bliver eleverne bedt om at forklare den anvendte ræsonnement eller at relatere en bestemt visuel metode til strategien, men IKKE i denne standard!
Den måde, jeg ser denne standard på, er, at lærerne skal LÆRE de forskellige nævnte strategier og derefter give eleverne SIMPLE additions- og subtraktionsopgaver inden for 20 som f.eks. 15 – 8 og 10 – 6. Jeg kan IKKE se, at denne standard kræver, at eleverne skal genkende, om en bestemt visuel model passer til en bestemt strategi.
Endnu en gang ser det ud til, at forfatteren smider sund fornuft ud … og faktisk ikke forstår standarderne.
Eksempel 4
Eksemplet nedenfor er meget dårligt formuleret, men KONCEPTet bag det er meget godt og findes også i Math Mammoth. Jeg kan derfor godt regne ud, hvad de vil have.
Du ser fem firkanter. Farv nogle blå og resten røde. Det er klart.
Før derefter firkanterne i “talbindingen” på samme måde. Talbindingen går til disse tre cirkler. Et barn, der har været til stede i en lektion, hvor læreren underviser i talbindinger, ved forhåbentlig, hvad det betyder. Det er det samme koncept som en faktafamilie … det øverste tal er summen eller totalen (5), og de tal, der går til de nederste cirkler, svarer til, hvor mange du har farvet blå og hvor mange røde, i dette tilfælde 1 og 4.
Så tror jeg, at de skjulte partnere også er 1 og 4. Vis 1 og 4 fingre til en voksen. Farvelæg til sidst 1 og 4 fingre på billedet (og ikke dine egne fingre, som det lyder som om).
Men efter min mening er den del om fingre superflous og forvirrende. Men begrebet talbindinger er meget ældre end CCS. Talbindinger er faktisk ikke nævnt i CCS, selv om de knytter sig til denne standard:
1.OA.4
Forstå subtraktion som et ukendt-addende problem. F.eks. subtrahere 10 – 8 ved at finde det tal, der giver 10, når det lægges sammen med 8.
og med dette
1.OA.6.
Addér og subtraherer inden for 20, idet du demonstrerer færdighed i addition og subtraktion inden for 10.
Jeg ved ikke, hvorfor dette regneark med talbindinger er angivet som et eksempel på Common Core Math. Det ville være meget bedre tituleret som et eksempel på et dårligt formuleret matematik-arbejdsark, der endda KUNNE stamme fra før Common Core (og som bare er genbrugt i netop dette pensum) … for som jeg sagde, er talbindinger IKKE nævnt i CCS.
Hvad Common Core Math Standards ikke er
- De er ikke “ny matematik”. Sammenlignet med mange matematiske læseplaner, der blev brugt i 2000’erne, som lagde vægt på ikke-traditionelle algoritmer, er CCS et klart skridt i retning af traditionelle algoritmer og udenadslære. Tjek disse specifikke standarder:
2.OA.2
Flydende addere og subtrahere inden for 20 ved hjælp af mentale strategier. Ved slutningen af 2. klasse kan de huske alle summer af to etcifrede tal.
Marias note: Dette er de grundlæggende additionsfakta, f.eks. 7 + 7 eller 5 + 4.3.OA.7
Flydende gange og dividere inden for 100 ved hjælp af strategier som f.eks. sammenhængen mellem multiplikation og division (f.eks. ved at vide, at 8 × 5 = 40, ved man, at 40 ÷ 5 = 8) eller egenskaber ved operationer. Ved slutningen af 3. klasse kan de huske alle produkter af to etcifrede tal.
Marias note: Dette betyder multiplikationstabeller og grundlæggende divisionsfakta.4.NBT.4
Flydende addere og subtrahere hele tal med flere cifre ved hjælp af standardalgoritmen.5.NBT.5
Flydende gange hele tal med flere cifre ved hjælp af standardalgoritmen.
Marias bemærkning: Dette betyder ikke, at eleverne kun skal gange hele tal med flere cifre i 5. klasse; det studeres også i 3. og 4. klasse. - Standarderne pålægger ikke lærere og elever mærkelige strategier eller visuelle modeller. Mange standarder overlader det til lærerne og eleverne selv. Eksempelvis:
2.NBT.5
Addér og subtraherer flydende inden for 100 ved hjælp af strategier, der er baseret på stedværdi, operationernes egenskaber og/eller forholdet mellem addition og subtraktion.Bemærk “og/eller” i ovenstående sætning. Det betyder, at lærerne og eleverne IKKE er begrænset til at bruge bestemte strategier og heller ikke bliver bedt om at bruge flere strategier. Den traditionelle “lånealgoritme” er en strategi, der er baseret på stedværdi, så den er medtaget lige her i 2.NBT.5.
2.NBT.9
Forklar, hvorfor additions- og subtraktionsstrategier fungerer, ved hjælp af stedværdi og operationernes egenskaber. Forklaringer kan understøttes af tegninger eller genstande.Der står “kan understøttes af tegninger”, men det tvinger dig ikke til at gøre det og begrænser dig heller ikke til at bruge en bestemt visuel model eller tegningstype.
3.OA.3
Anvender multiplikation og division inden for 100 til at løse ordproblemer insituationer, der involverer lige store grupper, arrays og målestørrelser,f.eks. ved at bruge tegninger og ligninger med et symbol for det ukendte tal til at repræsentere problemet.Den studerende SKAL ikke bruge en tegning. Det nævnes blot som en mulighed.
4.NBT.5
Multiplikere et helt tal på op til fire cifre med et etcifret helt tal og multiplicere to tocifrede tal ved hjælp af strategier baseret på stedværdi og operationernes egenskaber. Illustrere og forklare beregningen ved hjælp af ligninger, rektangulære arrays og/eller areamodeller.Læs “og/eller”. Illustrere beregningen, men det er tilstrækkeligt at illustrere den ved hjælp af ligninger. Du behøver ikke at illustrere den ved hjælp af arrays.
Det sagt, så nævner nogle standarder en specifik visuel model, såsom en tallinje eller en rektangulær arealmodel, men det er mindre almindeligt end at give et valg som i standarderne ovenfor.
Begrebsmæssig matematik
Der er nogle standarder, der kommer ind på den begrebsmæssige side af matematikken, som folkeskolelærere måske ikke forstår, hvis de ikke bliver undervist i, hvad de betyder; for eksempel:
5. NF.7b
Interpretere division af et helt tal med en enhedsbrøk og beregne sådanne kvotienter. Eksempelvis skabe en historiesammenhæng for 4 ÷ (1/5) og bruge en visuel brøkmodel til at vise kvotienten. Brug forholdet mellem multiplikation og division til at forklare, at 4 ÷ (1/5) = 20, fordi 20 × (1/5) = 4.
Et sådant historieproblem kunne være: Hvor mange stykker, der er 1/5 fod lange, kan du skære ud af et stykke materiale på 4 fod? En visuel model kunne vise 4 helheder, der er opdelt i femtedele. Vi kan så tælle, at 4 helheder har i alt 20 femtedele.
5.NF.4b
Find arealet af et rektangel med brøkdele af sidelængder ved at flise det med enhedsfirkanter med de relevante enhedsbrøkdele af sidelængder, ogvis, at arealet er det samme som det, der ville blive fundet ved at gange sidelængderne. Multiplicer brøkdele sidelængder for at finde arealer af rektangler, og fremstil brøkdelsprodukter som rektangulære arealer.
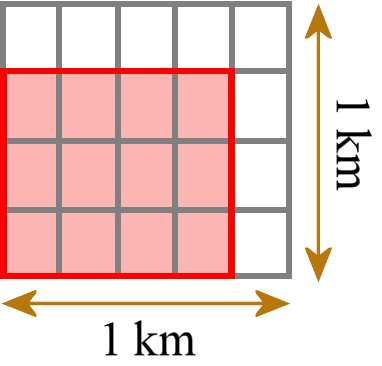Det vil f.eks. sige et rektangel med sidelængder på 3/4 km og 4/5 km. Derefter fliser vi det med små enhedsrektangler (ikke enhedsfirkanter; her har standarden selv den forkerte terminologi), der hver har sidelængderne 1/4 km og 1/5 km.
Vi kan tælle, hvor mange små fliser vi har brug for. Vi har brug for 12 sådanne fliser. Hver flise har et areal på 1/20 km2, så det samlede areal er 12/20 km2. Derefter kontrollerer vi og sammenligner, at vi får det samme svar, som hvis vi havde ganget de to sidelængder ved hjælp af almindelig brøkmultiplikation (3/4 km × 4/5 km = 12/20 km2).
Jeg har altid haft den slags problemer i mine bøger – også før CCS kom.
Nogle mennesker hævder, at børn ikke har brug for en sådan begrebsforståelse, eller at det er for svært. Personligt er jeg ikke enig. Jeg har altid (også før CCS) bestræbt mig på at forklare begreberne i brøkaritmetik, så eleverne ikke ender med at “følge reglerne blindt” og kun er i stand til at regne med brøker, hvis de tilfældigvis husker reglen korrekt. Jeg har altid lagt vægt på begrebsforståelse i matematik (som mine læsere ved!).
Men jeg håber, at du kan se, hvordan nogle af disse ting kan være uvante for skolelærere og forældre, og derfor er det ikke underligt, at det er svært for dem at følge Common Core Standards.
Det er mit håb, at Math Mammoth Light Blue Series og de enheder, jeg sælger i mine Teachers Pay Teachers- og Teachers’ Notebook-butikker, kan hjælpe de lærere & forældre, der har brug for Common Core-tilpassede materialer. Og som jeg sagde, kan resten af jer også være trygge ved at bruge dem. De indeholder ikke nogen “mærkelig” eller meningsløs matematik, men er som altid baseret på et solidt fundament af undervisning i matematiske begreber sammen med procedurerne.
Af Maria Miller