Eigenværdier er et særligt sæt af skalarer, der er forbundet med et lineært ligningssystem (i.e., en matrixligning), der undertiden også kaldes karakteristiske rødder, karakteristiske værdier (Hoffman og Kunze 1971), egentlige værdier eller latente rødder (Marcus og Minc 1988, s. 144).

Bestemmelsen af et systems egenværdier og egenvektorer er ekstremt vigtig inden for fysik og teknik, hvor den svarer til matrixdiagonalisering og forekommer i så almindelige anvendelser som stabilitetsanalyse, fysik for roterende legemer og små svingninger i vibrerende systemer, for blot at nævne nogle få. Hver egenværdi er parret med en tilsvarende såkaldt egenvektor (eller, generelt, en tilsvarende højre egenvektor og en tilsvarende venstre egenvektor; der er ingen analog sondring mellem venstre og højre for egenværdier).

Opdelingen af en kvadratisk matrix i egenværdier og egenvektorer er i dette arbejde kendt som egendekomposition, og det forhold, at denne opdeling altid er mulig, så længe den matrix, der består af egenvektorerne i , er kvadratisk, er kendt som egendekompositionssætningen.

Lanczos-algoritmen er en algoritme til beregning af egenværdier og egenvektorer for store symmetriske sparsomme matricer.

Lad være en lineær transformation, der er repræsenteret ved en matrix . Hvis der findes en vektor sådan at

(1)

for en vis skalar , så kaldes for egenværdien af med tilsvarende (højre) egenvektor .

Lad være en kvadratisk matrix

(2)

med egenværdi , så opfylder de tilsvarende egenvektorer

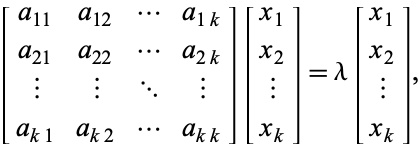(3)

som er ækvivalent med det homogene system

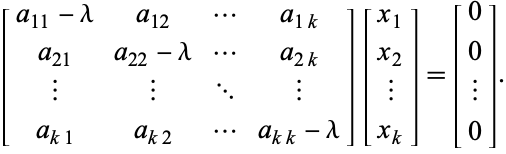(4)

Sammenligning (4) kan skrives kompakt som

(5)

hvor er identitetsmatrixen. Som det fremgår af Cramers regel, har et lineært ligningssystem ikke-trivielle løsninger, hvis determinanten forsvinder, så løsningerne til ligning (5) er givet ved

(6)

Denne ligning er kendt som den karakteristiske ligning for , og den venstre side er kendt som det karakteristiske polynomium.

For eksempel for en matrix , er egenværdierne

(7)

som fremkommer som løsningerne af karakteristicequation

(8)

hvis alle egenværdierne er forskellige, så får man ved at sætte disse ind igen uafhængige ligninger for komponenterne af hver tilsvarende egenvektor, og systemet siges at være ikke-degenereret. Hvis egenværdierne er -foldigt degenererede, siges systemet at være degenereret, og egenvektorerne er ikke lineært uafhængige. I sådanne tilfælde kan den yderligere begrænsning, at egenvektorerne skal være ortogonale,

(9)

hvor er Kronecker-deltaet, anvendes for at give yderligere begrænsninger, hvilket giver mulighed for løsning for egenvektorerne.

Eigenværdierne kan beregnes i Wolfram Language ved hjælp af egenværdierne. Egenvektorer og egenværdier kan returneres sammen ved hjælp af kommandoen Eigensystem.

Antag, at vi kender egenværdien for

(10)

Tilføjes en konstant gange identitetsmatrixen til ,

(11)

så de nye egenværdier er lig med de gamle plus . Multiplikation af med en konstant

(12)

så de nye egenværdier er de gamle ganget med .

Opnå en lighedstransformation af . Lad være determinanten af , så

			(13)
			(14)
			(15)

så egenværdierne er de samme som for .