
Galileo anses ofte for at være den moderne videnskabs fader. Han var den, der satte principperne for eksperiment, teori og matematik sammen i en standardramme. Sandsynligvis mere end nogen anden var Galilei den person, der var ansvarlig for udviklingen af den moderne videnskab.
Det siges, at Galilei lod to stålkugler med forskellig masse, men af samme materiale, falde ned fra det skæve tårn i Pisa, og de landede på samme tid. Det bemærkelsesværdige ved dette eksperiment er, at han indvarslede en ny metode til at lave videnskab, hvor man udfører et eksperiment for at afprøve en hypotese. Han viste, at vi skal gøre mere end blot at tro, at noget er sandt, men også at vi skal bevise det.

Galileo fandt et interessant paradoks, mens han var leder af det matematiske institut ved universitetet i Pisa.
Definition: Et paradoks, også kendt som en antinomi, er et logisk selvmodsigende udsagn eller et udsagn, der går imod ens forventning. (Wikipedia). (Græsk: “para” = hinsides, “doxa” = tro)
Galileos paradoks handlede om at afgøre, om to mængder, der indeholder uendeligt mange objekter, er ækvivalente med hinanden. Lad for eksempel P være mængden af positive hele tal, hvor P= {0,1,2,3,…} og E er mængden af lige tal, hvor E = {0,2,4,6,…}. Galilei hævdede, at størrelsen af disse to mængder vil være den samme, fordi vi kan parre hvert positivt heltal fra mængden P med de lige tal fra mængden E.

Så hvordan kan størrelsen af de to mængder være den samme, når et “mindre” tal optræder i E? Dette blev kaldt Galileos paradoks og startede en ny debat om begrebet uendelighed.
Efter Galileo blev hans elev Evangelista Torricelli leder af det matematiske institut ved universitetet i Pisa. Du har måske hørt om ham på grund af hans værker om atmosfærisk tryk og opfindelsen af barometeret. Da Toricelli også interesserer sig for matematik, spørger han:
Er det muligt at have en genstand med et endeligt rumfang og en uendelig overflade? For det første virker en sådan ting usandsynlig for de fleste af os. Matematikken fortæller os imidlertid, at en sådan ting kan ske. Torricelli besvarede selv sit spørgsmål og opdagede Toricelli’s trompet, hvis overflade er uendelig, men hvis volumen er endeligt. Hans opdagelse ses som et “utroligt” paradoks.
I øvrigt er der en væsentlig regel i matematikkens filosofi; Uanset hvilken æra inden for filosofi eller matematik man beskæftiger sig med, er den relateret til den pågældende regions historie, kultur og religion. Derfor kalder man Toricellis trompet også Gabriel’s Horn. Her henvises der til Bibelen, fordi kristne tror, at englen Gabriel vil blæse i hornet på dommedag.
Så hvordan dannes Toricellis trompet? Vi ved alle, hvordan man udarbejder en graf for y=x. Hvis man i stedet graferer ligningen y=1/x, hvor x er større eller lig med 1, vil grafen se således ud:
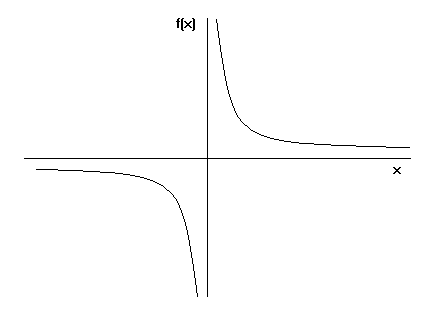
Når vi tager grafen for y=1/x og drejer den rundt om x-aksen, ser vi Toricellis trompet.

Godt nok har vi matematiske formler i hånden til at beregne arealet og volumenet af Toricellis trompet. Når vi anvender nedenstående integrationsformel for trompetens volumen, får vi et endeligt beløb.
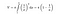
Men når vi anvender integrationsformlen for trompetens overfladeareal, bliver overfladen af den denne gang uendelig. Er dette resultat ikke interessant?
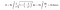
Da rumfanget af Toricellis trompet er endeligt, kan vi fylde den med en endelig mængde maling. Lad os for eksempel antage, at volumenet af den 100 liter. Jeg går til Home Depot og køber 100 liter maling og fylder den. Det, der gør det interessant, er imidlertid, at jeg vil have malet den uendelige overflade med de 100 liters maling. I dag kalder de fleste mennesker dette paradoks for “malerparadokset”.”
Houston, vi har et problem her! Den situation, der er umulig i praksis, bliver mulig i matematikken. Så hvordan kan Torricellis trompet være virkelig? Eller hvordan kan vi præcist matche alle elementerne i mængderne, mens en af mængderne er en delmængde af en anden i Galileos eksempel?
Grunden til alle disse konflikter er, at begrebet uendelighed ikke ligner andre begreber, som vi kender, og det forvirrer mange mennesker. Galilei siger om sit paradoks,
“Ja, min ven, der er uendelighed. Det er nyttesløst at gøre indsigelse mod det. De mængder, som jeg arbejder med, er eksempler på lukkede mængder, der involverer uendelighed. De starter ved et punkt og går videre til uendelighed, og alligevel er de stadig sæt. Mine kommentarer og begreber om uendelighed må dog være anderledes end dem, jeg ville bruge for endeløse størrelser. Hvis man har med finitte størrelser at gøre, kan man sige, at 3 kilo er mindre end 5 kilo, eller at 32 meter er længere end 7 meter. Men når det drejer sig om uendelighed, kan man ikke sige, at denne uendelighed er større, mindre eller lig med den.”
Det var Galileos løsning 1600-tallet.
Uheldigvis havde Galileos løsning sat gang i en ny debat om uendelighed. Matematikere og filosoffer kunne ikke blive enige om et specifikt svar, før Cantor delte sin “mængdelære”, som eleverne lærer i folkeskolen i dag.
Vi kan med jævne mellemrum historisere udviklingen af ideen om uendelighed. Den opstod først hos eleatikerne, som var en før-sokratisk filosofisk skole, der blev grundlagt af Parmenides i begyndelsen af det femte århundrede f.Kr. i den antikke by Elea. Der var tre store filosoffer i denne skole, såsom Zeno, Xenofanes og Parmenides. I denne skole var den accepterede filosofi, at eksistensen var singulær, og at der ikke var nogen flerhed. Zeno var berømt for sine paradokser om uendeligheden hos eleaterne. Senere i 300-tallet f.Kr.., opstod Aristoteles og foreslog et par begreber til at forklare Zenos paradokser, som var potentiel uendelighed og faktisk uendelighed.
Den potentielle uendelighed er en gruppe af tal eller en gruppe af “ting”, der fortsætter uden at afsluttes, fortsætter eller gentager sig selv igen og igen uden et genkendeligt slutpunkt.
Den faktiske uendelighed indebærer uendelige mængder eller “ting” inden for et rum, der har en begyndelse og en slutning; det er en serie, der teknisk set er “afsluttet”, men som består af et uendeligt antal medlemmer.
Aristoteles mente, at der ikke fandtes nogen faktisk uendelighed. Denne idé fra Aristoteles dominerede filosofiens verden indtil 1600-tallet. Derefter hævdede filosoffer som Cusa og Bruno, at der findes en faktisk uendelighed, men at vi ikke kan få mening ud af den. Efter Cuso og Bruno kom den store tænker Spinoza ind på emnet.
Spinoza sagde, at vi kunne forstå begrebet uendelighed og rangordne dem efter størrelse. Men han sagde også, at han ikke kunne regne dem ud. For eksempel kunne han tilføje 3 til 5, men han kunne ikke tilføje en uendelighed til en anden.
Endeligt, for at afslutte disse debatter, dukkede en smuk mand, Georg Cantor, op og fandt mængdelæren, som stadig er grundlaget for matematikken. Han satte det sidste punkt i uendelighedsdiskussionerne med sin mængdelære.
Han viste os, at en uendelighedsmængde ville være større eller mindre end en anden uendelighedsmængde. Desuden hævdede Cantor, at vi kunne addere og multiplicere uendelige mængder. Indtil da havde mennesket fulgt Aristoteles’ ideer om uendelighed. Ifølge Aristoteles ville tallet 3 blive uendeligt igen, hvis vi gangede det med uendeligt, hvis vi gangede det med uendeligt. Uendelighed ville opsluge alt. På baggrund heraf hævdede han, at der kun ville være potentiel uendelighed, ikke faktisk uendelighed.
Men Cantor beviste os imidlertid det modsatte af Aristoteles’ idé med mængdelæren. Hvis vi tilføjer en til en uendelig mængde, vil det ikke længere være den samme mængde. Han forsøgte at sammenligne de uendelige mængder. Cantor beviste f.eks., at mængden af alle funktioner fra (0,1)→ℕ er tællelig. Således definerede han en en-til-en- og onto-funktion fra intervallet (0,1) til naturlige tal.
Med andre ord beviste han, at alle naturlige tal kan passe mellem 0 og 1, fordi der var uendeligt mange rationale tal mellem 0-1, og disse uendeligheder kan parres sammen. Derefter gjorde han noget endnu farligere end at finde to lige store uendeligheder. Han sammenlignede uendeligheden af reelle tal med uendeligheden af naturlige tal og fandt ud af, at uendeligheden af reelle tal er større end den anden. Han kiggede endda på sit bevis og sagde til sin ven Dedekind: “Jeg kan se det, men selv jeg kan ikke tro det …”.
Cantor var også en matematiker med meget alvorlige filosofiske og religiøse bekymringer. Mens han udviklede mængdelæren, sagde han: “Gud dikterede mig mængdelæren”.
Mængdelæren var ikke bredt accepteret, da den først blev udviklet. Virksomhederne ansatte ikke engang Cantor til noget job. En matematiker, Henri Poincaré, sagde engang: “Denne Cantors ideer er en dårlig sygdom, der klistrer sig fast i matematikkens krave. Og matematikken vil behandle ham en dag”. Cantor måtte gå på et sindssygehospital i en periode og døde der. Men i dag anser vi ham for at være et geni.
Cantor var en ensom mand på kanten af uendeligheden. Han citerede Bibelen i begyndelsen af sin artikel om uendelige tal: “Alt, hvad der er skjult, vil blive bragt frem i lyset.”