I månedens tip (TOTM) fra november 2011 præsenterede vi beregningerne af kompressoren i en case study. Vi sammenlignede resultaterne fra den strenge metode med værdierne fra genvejsmetoderne. Den stringente metode var baseret på en tilstandsligning som Soave-Redlich-Kwong (SRK) til beregning af de nødvendige enthalpier og entropier. Enthalpierne og entropierne anvendes til at bestemme effektbehovet og udledningstemperaturerne. Resultaterne viste, at nøjagtigheden af den korte metode er følsom over for værdien af idealgastilstandens varmekapacitetsforhold, k.
Ud fra et beregningssynspunkt alene er effektberegningen særlig følsom over for specifikationen af massestrømningshastighed, sugetemperatur og -tryk samt afgangstemperatur og -tryk. En kompressor kommer til at fungere under varierende værdier af de variabler, der påvirker dens ydeevne. Den vanskeligste del af en kompressorberegning er således specifikationen af et rimeligt interval for hver variabel og ikke selve beregningen. Reference understreger, at anvendelse af en enkelt værdi for hver variabel ikke er den korrekte måde at evaluere et kompressionssystem på.
Normalt udføres de termodynamiske beregninger for en ideel (reversibel) proces. Resultaterne for en reversibel proces tilpasses derefter til den virkelige verden ved hjælp af en termodynamisk effektivitet. I kompressionsprocessen er der tre ideelle processer, som kan visualiseres: 1) en isotermisk proces (PV1=C1), 2) en isentropisk proces (PVk=C2) og 3) en polytropisk proces (PVn=C3). Enhver af disse processer kan på passende vis anvendes som grundlag for vurdering af kompressionseffektbehovet ved enten hånd- eller computerberegning. Den isotermiske proces anvendes dog sjældent som grundlag, fordi den normale industrielle kompressionsproces ikke engang tilnærmelsesvis foregår ved konstant temperatur.
Bemærk, at Dresser Rand arbejder en hel del med “næsten konstant temperatur”-kompression, især for CO2-kompression fra aftrækskaminer. For nærmere oplysninger henvises til:
I denne TOTM vil vi demonstrere, hvordan man kan bestemme effektiviteten af en kompressor ud fra målt flowhastighed, sammensætning, suge- og afgangstemperaturer og tryk. En stringent beregning baseret på en tilstandsligning og en genvejsmetode overvejes, og resultaterne sammenlignes.
Kompressoreffektivitet
Kompressorers efficiencer varierer med kompressortype, størrelse og gennemstrømning. De kan kun bestemmes (bagefter) ved en kompressortest, selv om kompressorproducenterne normalt kan give gode skøn. Til planlægningsformål foreslås som reference følgende værdier for de samlede efficiencer:
Tabel 1. Samlede kompressorvirkningsgrader
|
Kompressortype |
Effektivitet, η |
|
Centrifugal |
0.70 – 0,85 |
|
Høj hastighed frem- og tilbagegående |
0,72 – 0,85 |
|
Lav hastighed frem- og tilbagegående |
0.75 – 0,90 |
|
Rotary Screw |
0,65 – 0,75 |
Reference viser, at disse samlede efficiencer omfatter gasfriktion i kompressoren, de mekaniske tab (lejer, tætninger, gearkasse osv.) og gearkassetab. Den mekaniske efficiency varierer med kompressorstørrelse og -type, men 95 % er et nyttigt planlægningstal. Ved beregning af kompressorens højde og udblæsningstemperatur vil den anvendte efficiency være isentropisk eller polytropisk (isentropisk efficiency kaldes undertiden adiabatisk efficiency). Hvis man lægger 3-4 % efficiency (mekaniske tab) til de samlede efficiencer i tabel 1, får man generelt et godt skøn over den termodynamiske efficiency.
For at vurdere en eksisterende kompressors ydeevne er målet at beregne kompressorens virkningsgrad (η) og effektbehov.
Kendte og målte egenskaber er:
a. Gasmængden i standardtilstand (qS) eller gasmasseniveauet ()
b. Gassammensætning (zi)
c. Sugetryk (P1) og temperatur (T1)
d. Udstødningstryk (P2) og temperatur (T2)
Vurdering af virkningsgrad – stringent metode
Hjertet i enhver kommerciel software til simulering af processtrømme er en tilstandsligning. På grund af deres enkelhed og relative nøjagtighed anvendes en kubisk EOS som Soave Redlich-Kwong (SRK) eller Peng-Robinson. Disse ligninger anvendes til at beregne damp-væske-ligevægt (VLE), enthalpi (h) og entropi (s). Med de rette binære vekselvirkningskoefficienter er processimuleringsresultaterne for disse to ligninger praktisk talt de samme. Derfor er det kun SRK, der anvendes i dette arbejde.
Den isentropiske effektivitet er defineret ved
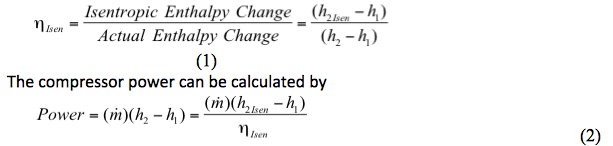
Hvor:
ηIsen = Isentropisk virkningsgrad
h1 = Suge entalpi beregnet ved P1, T1 og sammensætning (zi)
h2 = Udladnings entalpi beregnet ved P2, T2, og sammensætning (zi)
h2Isen = Isentropisk udladningsenthalpi ved P2 (eller T2), S2Isen =S1, og sammensætning (zi)
![]() = Massestrømningshastighed
= Massestrømningshastighed
Beregningen af kompressorens virkningsgrad eller effekt omfatter to trin
1. Bestemmelse af den ideelle eller isentropiske (reversible og adiabatiske) enthalpivandring (h2Isen-h1) i kompressionsprocessen.
2. Bestemmelse af den faktiske enthalpivandring (h2-h1).
Den trinvise beregning baseret på en EOS:
a. Antag stationær tilstand, dvs.
b. Antag, at foderets sammensætning forbliver uændret
c. Beregn sugeenthalpi h1=f(P1, T1 og zi) og entropi s1=f(P1, T1 og zi) ved EOS
d. Antag isentropisk proces, og sæt s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Beregn den ideelle enthalpi (h2Isen) ved udløbstilstand for kendte zi, T2 (eller P2) og s2Isen.
f. Beregn den faktiske enthalpi (h2) ved udløbsbetingelsen for kendte zi, T2 og P2.
g. Beregn den isentropiske virkningsgrad ved ligning 1: µIsen = (h2Isen – h1)/(h2 – h1)
h. Beregn effekten ved ligning 2: ![]()
Vurdering af virkningsgrad – genvejsmetode
Den isentropiske stieksponent (k) eller idealgasens varmekapacitetsforhold (k=CP/CV) kan beregnes ved hjælp af den korrelation, der blev præsenteret i TOTM fra maj 2013:
![]()
Hvor:
T = Temperatur, K (°R)
![]() = Gasens relative massefylde; forholdet mellem gassens molekylvægt og luftens molekylvægt
= Gasens relative massefylde; forholdet mellem gassens molekylvægt og luftens molekylvægt
A = 0.000272 (0.000151)
Den faktiske udledningstemperatur baseret på en isentropisk vej kan estimeres ved

at løse op for den isentropiske effektivitet,
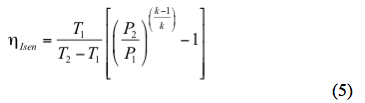
Sådan, kan den faktiske udledningstemperatur baseret på en polytropisk vej estimeres ved

Løsning af ovenstående ligning for den polytropiske vejkoefficient (n):

På samme måde kan den faktiske udledningstemperatur baseret på en polytropisk sti estimeres (ηPoly) ved at:

Det isentropiske fald beregnes ved
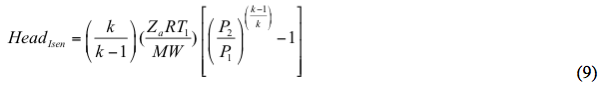
Sådan, beregnes det polytropiske hoved ved
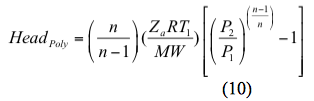
For en isentropisk (reversibel og adiabatisk) proces beregnes effekten ved
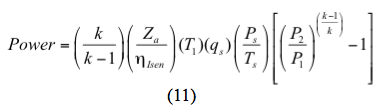
Og for en polytropisk proces beregnes effekten ved
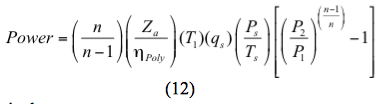
Alternativt:
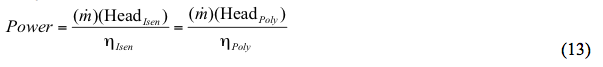
Hvor:
Højde = Kompressorhøjde, m (ft)
Effekt = Kompressoreffekt, kW (HP)
R = Universel gaskonstant, 848 kg-m/(kmol-K) eller (1545 ft-lbf/(lbmol-°R))
PS = Standardtryk i standardtilstand, kPa (psia)
P1 = Sugetryk, kPa (psia)
P2 = Udstødningstryk, kPa (psia)
TS = Standardbetingelsestemperatur, K (°R)
T1 = Sugetemperatur, K (°R)
T2 = Udstødningstemperatur, K (°R)
qS = Gasvolumenmængde ved standardbetingelse, Sm3/d (scf/dag)
Za = Gennemsnitlig gaskompressibilitetsfaktor = (Z1+Z2)/2
Z1 = Gaskompressibilitetsfaktor ved sugebetingelse
Z2 = Gaskompressibilitetsfaktor ved udløbsbetingelse
MW = Gasmolekylvægt
Effektberegningen skal foretages pr. kompressionstrin og derefter summeres for alle trin, der er tilsluttet en enkelt driver.
Trin-for-trin-beregningen for genvejsmetoden
a. Beregn den isentropiske eksponent (k) ved ligning 3 ved hjælp af den gennemsnitlige temperatur defineret ved T = (T1+3T2)/4. Denne form for gennemsnitstemperatur blev defineret for at opnå bedre overensstemmelse mellem de strenge resultater og resultaterne af genvejmetoden.
b. Beregn den isentropiske effektivitet (ηIsen) ved hjælp af ligning 5.
c. Beregn den polytropiske koefficient (n) ved ligning 7.
d. Beregn den polytropiske effektivitet (ηPoly) ved ligning 8.
e. Beregn det isentropiske og polytropiske opløb ved hjælp af henholdsvis ligning 9 og 10.
f. Beregn den nødvendige effekt pr. trin ved hjælp af enten ligning 11 eller 12.
Casestudie
En naturgasblanding komprimeres ved hjælp af en tretrins centrifugalkompressor. Procesflowdiagrammet er vist i figur 1. For hvert trin er det målte tryk og den målte temperatur angivet i tabel 1. Den målte indføringssammensætning, flowhastigheder og den beregnede molekylvægt og relative massefylde er angivet i tabel 2.
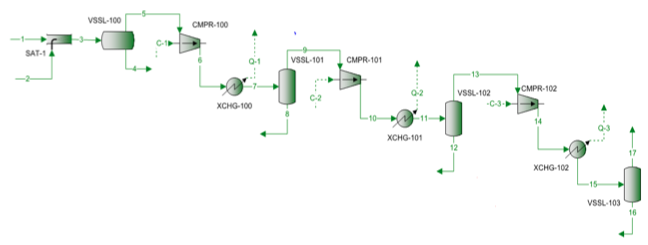
Figur 1. Procesflowdiagram for en 3-trins kompression
Tabel 1. Målt temperatur og tryk for de tre kompressionsfaser
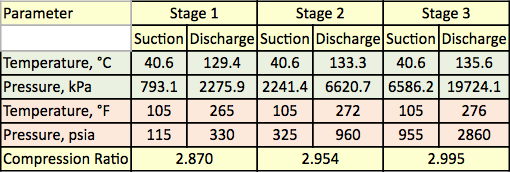
Tabel 2. Gasanalyse og flowhastighed for de tre kompressionstrin
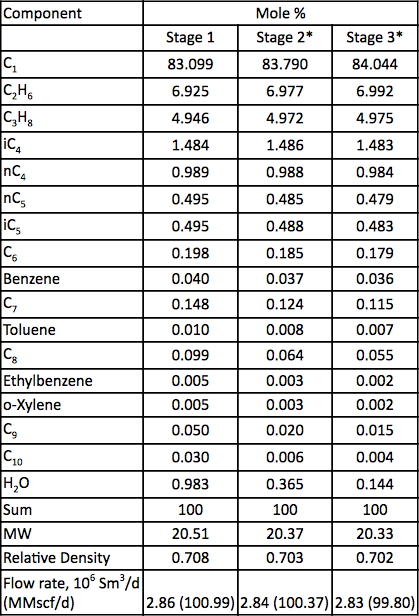
* Beregnet
Resultater og diskussioner
Det procesflowdiagram, der er vist i figur 1, blev simuleret med ProMax-software for at udføre de strenge beregninger ved hjælp af SRK EOS. Programmet beregnede polytropiske og isentropiske virkningsgrader, heads og kompressionseffekt. Programmet beregnede også den isentropiske eksponent (k) og den polytropiske eksponent (n). Disse beregnede resultater er vist i tabel 2 for alle tre trin under SRK-rubrikker. De beregninger, der udføres af ProMax, svarer meget til de trinvise beregninger af a til h, der er beskrevet i det strenge afsnit. Tabel 2 viser også resultaterne af genvejskalkulationen for de tilsvarende værdier under genvejsposten. Genvejsberegningerne er baseret på den trinvise beregning af a til f, der er beskrevet i afsnittet om genvejsmetoden. Fejlprocenten mellem den stringente metode og genvejsmetoderne for hvert trin er også anført i tabel 2. Tabel 2 viser, at der opnås fremragende overensstemmelse for trin 1 og 2. Der konstateres dog større afvigelser for de isetrope og polytrope eksponenter for trin 3 på grund af højtryksdrift, som afviger for langt fra de ideelle gastilstandsbetingelser.
Tabel 3. Sammenfatning af de rigoristiske og genvejsberegnede resultater
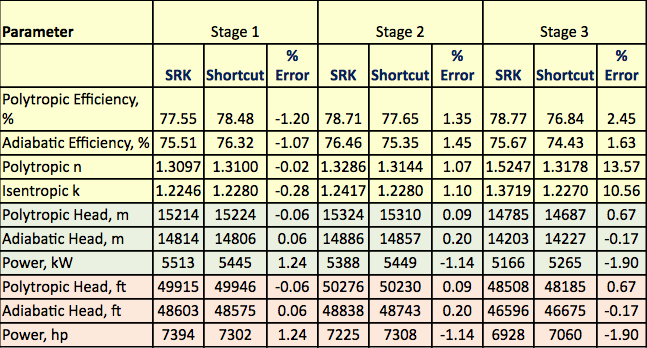
Slutninger
Tabel 2 viser, at der er god overensstemmelse mellem de genvejsberegnede og de rigoristiske resultater. Forskellene mellem de stringente resultater og resultaterne af den korte metode til beregning af anlæg og planlægningsformål er ubetydelige. For fase 3 observeres en større fejl for den isentropiske eksponent (k) på grund af højtryksdrift og for stor afvigelse fra den ideelle gastilstandsbetingelse.
Den beregnede isentropiske eksponent (k) i ProMax er ikke det ideelle gastilstands varmekapacitetsforhold (CP/CV) i gastilstanden. Det er den værdi af den isentropiske eksponent, der er nødvendig for at give en isentropisk vej fra indløb til udløb. Dens værdi beregnes som en integration af denne vej. Der er således tale om en slags “gennemsnitsværdi”, der repræsenterer den sande isentropiske vej. For ideelle gasser ville værdien være lig med (CP/CV)-forholdet.
Denne fejl i “k” illustrerer også vigtigheden af at specificere, hvilken korrelation der skal anvendes, når man bestiller en præstationstest (dvs. se ASME PTC-10 for yderligere oplysninger), så kunden og leverandøren er enige om at gå videre med hensyn til molekylvægt (MW) og k for testvæsken. For yderligere detaljer henvises til referencen og TOTM’erne fra august og september 2010.
Det kan også være værd at bemærke, at når man ved at opstille en trend for “n” og den polytrope effektivitet for at evaluere maskinens tilstand, introducerer den relative nøjagtighed af måleinstrumenter/udstyr (temperatur- og tryktransducere) og kortlægning af kompressorens ydeevne til den oprindelige ydelseskurve (faktisk gasvolumenstrømningshastighed vs. hastighed) mange potentielle fejlkilder i denne daglige evaluering.
Bemærk, at nøjagtigheden af genvejsmetoderne er afhængig af værdierne for k og n. Definitionen af gennemsnitstemperaturen i genvejsmetoden blev justeret for at opnå en bedre overensstemmelse mellem den isentropiske vejeksponent (k) beregnet ved den strenge metode.
For at lære mere om lignende tilfælde og om, hvordan man minimerer driftsproblemer, foreslår vi, at du deltager i vores kurser G4 (Gaskonditionering og -behandling), PF4 (Olieproduktions- og -behandlingsanlæg), ME46 (Kompressorsystemer – mekanisk design og specifikationer) og ME44 (Grundlæggende principper for pumpe- og kompressorsystemer).
PetroSkills tilbyder konsulentekspertise om dette emne og mange andre. For yderligere oplysninger om disse tjenester, besøg vores websted på http://petroskills.com/consulting, eller send os en e-mail på [email protected].
Dr. Mahmood Moshfeghian
Reference:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., og Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, s. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, “Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J. “Vigtige aspekter af prøvning af centrifugalkompressorer – del 1”, månedens tip, august 2010
8. Honeywell, J. “Vigtige aspekter af prøvning af centrifugalkompressorer – del 2”, månedens tip, september 2010
8.