Forestil dig en firkant af papir, der ligger fladt på dit skrivebord. Jeg beder dig om at lukke øjnene. Du hører papiret skifte. Når du åbner øjnene, ser papiret ikke ud til at have ændret sig. Hvad kan jeg have gjort ved det, mens du ikke kiggede?
Det er indlysende, at jeg ikke har drejet papiret 30 grader, for så ville papiret se anderledes ud.

Jeg har heller ikke vendt det på tværs af en linje, der forbinder f.eks. et af hjørnerne med midtpunktet af en anden kant. Papiret ville se anderledes ud, hvis jeg havde gjort det.

Det, jeg kunne have gjort, var imidlertid at dreje papiret med eller mod uret med et vilkårligt multiplum af 90 grader, eller vende det på tværs af en af de diagonale linjer eller de vandrette og lodrette linjer.
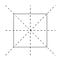
En nyttig måde at visualisere transformationerne på er at markere firkantens hjørner.

Den sidste mulighed er, at man ikke gør noget. Dette kaldes identitetstransformationen. Tilsammen kaldes alle disse for symmetritransformationer af kvadratet.
Jeg kan kombinere symmetritransformationer til andre symmetritransformationer. F.eks. giver to vendinger på tværs af linjestykket BD identiteten, ligesom fire på hinanden følgende rotationer på 90 grader mod uret giver identiteten, ligesom fire på hinanden følgende rotationer på 90 grader mod uret. En vending om den lodrette linje efterfulgt af en vending om den vandrette linje har den samme sikre virkning som en 180 graders rotation. Generelt vil enhver kombination af symmetritransformationer give en symmetritransformation. Følgende tabel giver reglerne for sammensætning af symmetritransformationer:

I denne tabel betegner R med subscripts 90, 180 og 270 rotationer mod uret med 90, 180 og 270 grader, H betyder en vending om den vandrette linje, V er en vending om den lodrette linje, MD er en vending om diagonalen fra øverst til venstre til nederst til højre, og OD betyder en vending over den anden diagonal. For at finde produktet af A og B skal man gå til rækken for A og derefter over til kolonnen for B. For eksempel: H∘MD=R₉₉₀.
Der er et par ting, du måske bemærker ved at se på tabellen:
- Operationen ∘ er associativ, hvilket betyder, at A∘(B∘C) = (A∘B)∘C for alle transformationer A, B og C.
- For ethvert par af symmetritransformationer A og B er sammensætningen A∘B også en symmetritransformation
- Der er et element e sådan, at A∘e=e∘A for enhver A
- For enhver symmetritransformation A, er der en unik symmetritransformation A-¹ sådan, at A∘A-¹=A-¹∘A=e
Vi siger derfor, at samlingen af symmetritransformationer af et kvadrat, kombineret med komposition, danner en matematisk struktur, der kaldes en gruppe. Denne gruppe kaldes D₄, den dihedrale gruppe for kvadratet. Disse strukturer er emnet for denne artikel.
Definition af en gruppe
En gruppe ⟨G,*⟩ er en mængde G med en regel * for kombination af to vilkårlige elementer i G, der opfylder gruppeaksiomerne:
I det abstrakte undertrykker vi ofte * og skriver a*b som ab og refererer til * som multiplikation.

Det er ikke nødvendigt, at * er kommutativt, dvs. at a*b=b*a. Det kan man se ved at se på tabellen for D₄, hvor H∘MD=R₉₀, men MD∘H=R₂₇₀. Grupper, hvor * er kommutativ, kaldes abelske grupper efter Neils Abel.
Abeliske grupper er undtagelsen snarere end reglen. Et andet eksempel på en ikke-abelsk gruppe er symmetriske transformationer af en terning. Overvej blot rotationer om akserne:
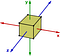
Hvis jeg først roterer 90 grader mod uret om y-aksen og derefter 90 grader mod uret om z-aksen, så vil hans få et andet resultat, end hvis jeg først roterer 90 grader om z-aksen og derefter 90 grader om y-aksen.

Det er muligt for et element at være sin egen inverse. Betragt gruppen, som består af 0 og 1 med operationen binær addition. Dens tabel er:

Det er klart, at 1 er sin egen inverse. Dette er også en abelsk gruppe. Bare rolig, de fleste grupper er ikke så kedelige.
Der er flere eksempler på grupper:
- Mængden af hele tal med addition.
- Mængden af rationale tal uden 0 med multiplikation.
- Mængden af løsninger til polynomielligningen xⁿ-1=0, kaldet de n’te rødder af enhed, med multiplikation.
Her er nogle eksempler, som ikke er grupper:
- Mængden af de naturlige tal under addition er ikke en gruppe, fordi der ikke er nogen omvendte, hvilket ville være de negative tal.
- Mængden af alle rationale tal inklusive 0 under multiplikation er ikke en gruppe, fordi der ikke findes noget rationalt tal q, for hvilket 0/q=1, så ikke hvert element har en invers.
Gruppestruktur
En gruppe er meget mere end blot en klat, der opfylder de fire aksiomer. En gruppe kan have en intern struktur, og denne struktur kan være meget indviklet. Et af de grundlæggende problemer i abstrakt algebra er at bestemme, hvordan den interne struktur i en gruppe ser ud, da de grupper, der faktisk studeres i den virkelige verden, er meget større og mere komplicerede end de simple eksempler, vi har givet her.
En af de grundlæggende typer af intern struktur er en undergruppe. En gruppe G har en undergruppe H, når H er en delmængde af G og:
- For a,b∈H, a*b∈H og b*a∈H
- For a∈H, a-¹∈H
- Den identiteten er et element af H
Hvis H≠G, så siges H at være en proper undergruppe. Den undergruppe af G, der kun består af identiteten, kaldes den trivielle undergruppe.
En ikke-abelsk gruppe kan have kommutative undergrupper. Overvej den kvadratiske dihedralgruppe, som vi diskuterede i indledningen. Denne gruppe er ikke abelsk, men undergruppen af rotationer er abelsk og cyklisk:
Vi giver nu to eksempler på gruppestruktur.
Selv om en gruppe G ikke er abelsk, kan det stadig være tilfældet, at der findes en samling af elementer i G, der kommuterer med alt i G. Denne samling kaldes centrum for G. Centrum C er en undergruppe af G. Bevis:
Nu antages det, at f er en funktion, hvis domæne og område begge er G. En periode af f er et element a∈G, således at f(x)=f(ax) for alle x∈G. Mængden P af perioder af f er en undergruppe af G. Bevis:
Finitte grupper er endeligt genererede
Vi så, at cykliske grupper er genereret af et enkelt element. Når det er muligt at skrive hvert element i en gruppe G som produkter af en (ikke nødvendigvis proper) delmængde A af G, så siger vi, at A genererer G, og skriver dette som G=⟨A⟩. Det mest “nå, duh”-bevis, du nogensinde vil se, er beviset for, at alle finitte grupper genereres af en finit genererende mængde:
- Lad G være finit. Hvert element i G er et produkt af to andre elementer i G, så G=⟨G⟩. QED.

Vi vil afslutte denne artikel med en anvendelse.
Fejlresistent kommunikation
Den enkleste måde at transmittere digital information på er at kode den i binære strenge af fast længde. Ingen kommunikationsordning er helt fri for forstyrrelser, så der er altid en mulighed for, at de forkerte data vil blive modtaget. Metoden med maksimal sandsynlighedsafkodning er en enkel og effektiv metode til at opdage og korrigere overførselsfejl.
Lad 𝔹ⁿ være mængden af binære strenge, eller ord, af længde n. Det er ligetil at vise, at 𝔹ⁿ er en abelsk gruppe under binær addition uden overføring (således at f.eks. 010+011=001). Bemærk, at hvert element er sin egen inverse. En kode C er en delmængde af 𝔹ⁿ. Følgende er et eksempel på en kode i 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Eelementerne i en kode kaldes kodeord. Kun kodeord vil blive transmitteret. Man siger, at der opstår en fejl, når interferens ændrer en bit i et transmitteret ord. Afstanden d(a,b) mellem to kodeord a og b er det antal cifre, hvori to kodeord adskiller sig fra hinanden. Den mindste afstand for en kode er den mindste afstand mellem to kodeord. For eksempelkoden lige ovenfor er minimumsafstanden tre.
I metoden til afkodning med maksimal sandsynlighed skal modtageren, hvis vi modtager et ord x, som kan indeholde fejl, fortolke x som kodeordet a, således at d(a,x) er et minimum. Jeg vil vise, at for en kode med minimal afstand m kan dette altid (1) opdage fejl, der ændrer færre end m bits, og (2) korrigere fejl, der ændrer ½(m-1) eller færre bits.

I vores eksempelkode er m=3 og kuglen med radius ½(m-1)=1 om kodeordet 011101 {01110101, 11110101, 00110101, 011001, 010101, 011111, 011111, 011100}. Så hvis modtageren modtager et af disse ord, ved den, at det var meningen, at den skulle have modtaget 011101.
Så det er alt sammen godt og vel, men hvad har alt dette at gøre med gruppeteori? Svaret ligger i, hvordan vi rent faktisk producerer de koder, som denne metode arbejder med.
Det er muligt for en kode i 𝔹ⁿ at danne en undergruppe. I dette tilfælde siger vi, at koden er en gruppekode. Gruppekoder er finitte grupper, så de er endeligt genererede. Vi vil se, hvordan man kan frembringe en kode ved at finde en genererende mængde.
En kode kan specificeres således, at de første par bits i hvert kodeord kaldes informationsbits, og at de bits, der ligger i slutningen, kaldes paritetsbits. I vores eksempelkode C er de tre første bits informationsbits og de tre sidste bits paritetsbits. Paritetsbitsene opfylder paritetstjekligningerne. For et kodeord A₁A₂A₃A₄A₅A₆ er paritetsligningerne A₄=A₁+A₂, A₅=A₂+A₃, og A₆=A₁+A₃. Paritetsligningerne giver endnu et lag af beskyttelse mod fejl: Hvis en af paritetsligningerne ikke er opfyldt, er der opstået en fejl.
Her er, hvad vi gør. Lad os antage, at vi ønsker kodeord med m informationsbits og n paritetsbits. For at generere en gruppekode skal du skrive en matrix med m rækker og m+n kolonner. I den blok, der er dannet af de første m kolonner, skrives den m×m identitetsmatrix. I kolonne j for m+1≤j≤m_n skrives en 1 i den k-te række, hvis Aₖ forekommer i paritetsligningen for paritetsbit Aⱼ, og 0 ellers. I vores eksempelkode er matricen:

En sådan matrix kaldes en genererende matrix for gruppekoden. Man kan direkte verificere, at rækkerne genererer C:

Rækkerne i en hvilken som helst genererende matrix danner et genererende sæt for en gruppekode C. Bevis:
- Identitet og inverser: Enhver række adderet til sig selv giver identiteten, en streng bestående af alle nuller.
- Slutning: Hvis A,B∈C, så er A og B summer af rækker i den genererende matrix, så A+B er også en sum af rækker i den genererende matrix. Derfor A+B∈C.
Derved kan vi generere en kode, nu vil jeg vise, hvordan man genererer en brugbar kode.
Definér vægten w(x) til at betyde antallet af ettaller i x. For eksempel w(100101)=3. Det er indlysende, at w(x)=d(x,0), hvor 0 er et ord, hvis cifre alle er nuller. Den mindste vægt W i en kode er vægten af det kodeord, der ikke er nul, og som har færrest ettaller i koden. For en kode med mindste afstand m er d(x,0)≥m, så w(x)≥m, og derfor er W=m.
Husk, at for at et ord kan betragtes som et kodeord, skal det opfylde et sæt paritetskontrolligninger. For vores eksempelkode er disse A₄=A₁+A₂, A₅=A₂+A₃, og A₆=A₁+A₃. Vi kan også skrive disse som et lineært system:
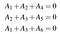
Som selv kan skrives i form af punktprodukter:

Og i mere kompakt form som Ha=0, hvor a=(A₁,A₂,A₃,A₄,A₅,A₆) og H er paritetskontrolmatrixen for koden:

Man kan verificere ved direkte beregning, at hvis w(a)≤2, så kan vi ikke have Ha=0. Generelt er den mindste vægt t+1, hvor t er det mindste tal, således at enhver samling af t kolonner i H ikke summerer til nul (dvs. at de er lineært uafhængige). At bevise dette ville føre os lige lidt for langt ind i lineær algebra.
Hvis det skræmmer dig, skal du ikke være bekymret. Vi kan fremstille nogle meget gode koder uden det ved at udnytte det faktum, at det resultat, jeg lige har nævnt, indebærer, at hvis hver kolonne i H er ikke-nul, og ingen to kolonner er lige store, så er minimumsvægten, og dermed kodens minimumsafstand, mindst tre. Dette er meget godt: Hvis vores kommunikationssystem forventes at have en bitfejl for hvert hundrede transmitterede ord, så vil kun et ud af ti tusind transmitterede ord have en ukorrigeret fejl, og et ud af en million transmitterede ord vil have en uopdaget fejl.
Så nu har vi en opskrift på at fremstille en brugbar kode til maximum-likelihood-detektionsordningen for kodeord, der indeholder m informationsbits og n paritetsbits:
- Skab en matrix med m+n kolonner og n rækker. Udfyld matricen med ettaller og nuller, således at ingen kolonner er ens, og ingen kolonne kun består af nuller.
- Hver række i den resulterende paritetskontrolmatrix svarer til en af paritetsbitligningerne. Skriv dem som et system af ligninger, og løs dem, så hver paritetsbit skrives i form af informationsbits.
- Opret en matrix med m+n kolonner og m rækker. I den blok, der er dannet af de første m kolonner, skal du skrive den m×m identitetsmatrix. I kolonne j for m+1≤j≤m_n skrives et 1 i den k-te række, hvis Aₖ optræder i paritetsligningen for paritetsbit Aⱼ og 0 ellers.
- Rækkerne i denne matrix er generatorerne i en kodegruppe med en mindste afstand på mindst tre. Dette er den kode, vi skal bruge.
Som eksempel kan vi antage, at jeg har brug for en simpel kode med otte ord, og at jeg kun har brug for noget grundlæggende fejlfinding og ikke korrektion, så jeg kan slippe af sted med en minimumsafstand på to. Jeg ønsker tre informationsbits og to paritetsbits. Jeg skriver følgende paritetskontrolmatrix ned:
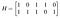
Der er to kolonnepar, der er lige store, så det mindste t, for hvilket enhver samling af t kolonner er lineært uafhængig, er ét, så den mindste vægt, og dermed den mindste afstand, jeg vil have, er to. Rækkerne repræsenterer paritetskontrolligningerne A₄=A₁+A₃ og A₅=A₁+A₂+A₃. Min genererende matrix er derfor:

Og rækkerne i denne matrix genererer kodegruppen:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Sluttende bemærkninger
Abstrakt algebra er et dybt emne med vidtrækkende konsekvenser, men det er også meget let at lære. Bortset fra nogle få forbigående omtaler af lineær algebra er næsten alt, hvad jeg har diskuteret her, tilgængeligt for en person, der kun har haft algebra på gymnasiet.
Da jeg først fik ideen til at skrive denne artikel, ville jeg egentlig gerne tale om Rubiks terning, men i sidste ende ville jeg vælge et eksempel, der kun kunne dækkes med de mest grundlæggende ideer i gruppeteori. Desuden er der så meget at sige om Rubiks terningegruppe, at den fortjener en selvstændig artikel, så den kommer snart.
Mine college-kurser i abstrakt algebra var baseret på bogen A Book of Abstract Algebra af Charles Pinter, som er og tilgængelig behandling. Eksemplerne i denne artikel er alle lånt med visse ændringer fra Pinter.
Som en sidste bemærkning, er alle billeder, der ikke er citeret, mit eget originale arbejde og må bruges med kildeangivelse. Som altid sætter jeg pris på eventuelle rettelser eller anmodninger om præciseringer.