I lighed med P-only-regulatoren beregner og sender Proportional-Integral (PI)-algoritmen et regulatorudgangssignal (CO) for hver prøvetid, T, til det endelige reguleringselement (f.eks. ventil, pumpe med variabel hastighed). Det beregnede CO-signal fra PI-algoritmen påvirkes af regulatorens indstillings parametre og regulatorfejlen e(t).
PI-regulatorer har to indstillings parametre, der skal justeres. Selv om dette gør dem mere udfordrende at indstille end en P-only-regulator, er de ikke så komplekse som PID-regulatoren med tre parametre.
Integral handling gør det muligt for PI-regulatorer at eliminere offset, som er en stor svaghed ved en P-only-regulator. PI-regulatorer giver således en balance mellem kompleksitet og kapacitet, der gør dem til langt den mest udbredte algoritme i procesreguleringsapplikationer.
PI-algoritmen
Mens forskellige leverandører støber det, der i alt væsentligt er den samme algoritme, i forskellige former, undersøger vi her det, der på forskellig vis beskrives som den afhængige, ideelle, kontinuerlige, positionsform:
![]()
Hvor:
CO = reguleringens udgangssignal (ledningen ud)
CObias = reguleringens bias eller nulværdi; indstillet ved hjælp af ubelastet overførsel som forklaret nedenfor
e(t) = aktuel reguleringsfejl, defineret som SP – PV
SP = setpunkt
PV = målt procesvariabel (ledningen ind)
Kc = reguleringsforstærkning, en indstillingsparameter
Ti = nulstillingstid, en indstillingsparameter
De to første udtryk til højre for lighedstegnet er identiske med den P-Only-regulator, der henvises til øverst i denne artikel.
Regulatorens integraltilstand er det sidste udtryk i ligningen. Dens funktion er at integrere eller løbende summere reguleringsfejlen, e(t), over tid.
Nogle ting, vi bør vide om afstemnings parameteren for nulstillingstid, Ti:
| ▪ | Den giver en separat vægt til det integrale udtryk, så indflydelsen af den integrale handling kan justeres uafhængigt. |
| ▪ | Det er i nævneren, så mindre værdier giver en større vægt til (dvs. øger indflydelsen af) det integrale udtryk. |
| ▪ | Det har tidsenheder, så det er altid positivt. |
Funktionen af den proportionale term
Som med P-only-regulatoren tilføjer eller fratrækker PI-regulatorens proportionale term, Kc-e(t), fra CObias baseret på størrelsen af reguleringsfejlen e(t) til hvert tidspunkt t.
Som e(t) vokser eller skrumper, vokser eller skrumper det beløb, der føjes til CObias, straks og proportionelt. Den tidligere historie og den aktuelle bane for reguleringsfejlen har ingen indflydelse på beregningen af den proportionale term.
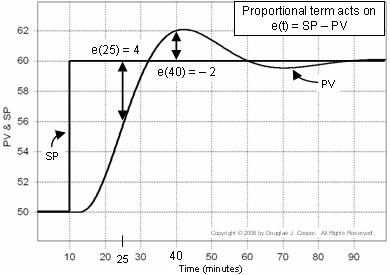
Det nedenstående plot (klik for en stor visning) illustrerer denne idé for en setpunktsrespons. Den fejl, der anvendes i proportionalitetsberegningen, er vist på plottet:
▪ Til tiden t = 25 min, e(25) = 60-56 = 4
▪ Til tiden t = 40 min, e(40) = 60-62 = -2
Idet vi erindrer om, at reguleringsfejl e(t) = SP – PV, kan vi i stedet for at betragte PV og SP som separate spor, som vi gør ovenfor, beregne og plotte e(t) på hvert punkt i tiden t.
Nedenfor (klik for en større visning) er de samme data som ovenfor, blot er de omformet som et plot af e(t) selv. Bemærk, at i plottet ovenfor er PV = SP = 50 for de første 10 min, mens der i fejlplottet nedenfor er e(t) = 0 for samme tidsperiode.
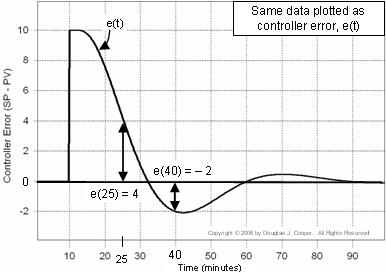
Dette plot er nyttigt, da det hjælper os med at visualisere, hvordan reguleringsfejl løbende ændrer størrelse og fortegn, efterhånden som tiden går.
Funktionen af den integrale term
Mens den proportionale term kun tager hensyn til den aktuelle størrelse af e(t) på tidspunktet for reguleringsberegningen, tager den integrale term hensyn til fejlens historik, eller hvor længe og hvor langt den målte procesvariabel har været fra setpunktet over tid.
Integration er en kontinuerlig summering. Integration af fejl over tid betyder, at vi summerer hele reguleringsfejlhistorikken frem til det aktuelle tidspunkt, startende fra det tidspunkt, hvor regulatoren først blev skiftet til automatisk.
Reguleringsfejl er e(t) = SP – PV. I nedenstående plot (klik for en stor visning) beregnes den integrale sum af fejl som de skraverede områder mellem SP- og PV-sporene.
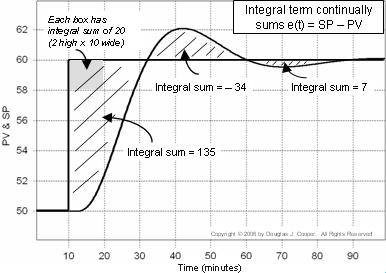
Hver kasse i plottet har en integral sum på 20 (2 højt og 10 bredt). Hvis vi tæller antallet af kasser (herunder brøkdele af kasser), der er indeholdt i de skraverede områder, kan vi beregne den integrale sum af fejl.
Så når PV først krydser setpunktet omkring t = 32, er den integrale sum vokset til ca. 135. Vi skriver PI-regulatorens integraludtryk som:
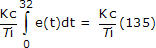
Da det er reguleringsfejl, der driver beregningen, får vi et direkte overblik over situationen fra et reguleringsfejlplot, som vist nedenfor (klik for stor visning):

Opmærksomheden henledes på, at integralet af hvert skraveret område har samme fortegn som fejlen. Da integralsummen begynder at akkumuleres, når regulatoren først sættes i automatik, vokser den samlede integralsum, så længe e(t) er positiv, og den skrumper, når den er negativ.
Til tiden t = 60 min på plottet er integralsummen 135 – 34 = 101. Responsen er stort set udlignet ved t = 90 min, og integralsummen er da 135 – 34 + 7 = 108.
Integralvirkning eliminerer forskydning
Den foregående sætning indeholder en subtil, men meget vigtig observation. Svaret er stort set færdigt på tidspunktet t = 90 min, men alligevel er den integrale sum af alle fejl ikke nul.
I dette eksempel har den integrale sum en endelig eller residual værdi på 108. Det er denne restværdi, der gør det muligt for PI-regulatorens integralvirkning at eliminere offset.
Som omtalt i en tidligere artikel oplever de fleste processer under P-only-regulering offset under normal drift. Offset er en vedvarende værdi for reguleringsfejl (dvs. PV er ikke lig med SP ved stationær tilstand).
Vi genkender fra P-Only-reguleringen:
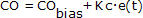
at CO altid vil være lig med CObias, medmindre vi tilføjer eller trækker noget fra det.
Den eneste måde, hvorpå vi har noget at tilføje eller trække fra CObias i P-Only-ligningen ovenfor, er, hvis e(t) ikke er nul. Hvis e(t) ikke er konstant på nul, er PV ikke lig med SP, og vi har offset.
Men med PI-regulatoren:
![]()
Vi ved nu, at den integrale sum af fejl kan have en slut- eller restværdi, efter at en reaktion er afsluttet. Dette er vigtigt, fordi det betyder, at e(t) kan være nul, men at vi stadig kan have noget at tilføje eller trække fra CObias for at danne det endelige reguleringsoutput, CO.
Så længe der er en fejl (så længe e(t) ikke er nul), vil det integrale udtryk vokse eller skrumpe i størrelse for at påvirke CO. Ændringerne i CO vil først ophøre, når PV er lig med SP (når e(t) = 0) i en længere periode.
På det tidspunkt kan den integrale term have en restværdi, som netop diskuteret. Denne restværdi fra integrationen, når den lægges til CObias, skaber i det væsentlige en ny samlet bias-værdi, der svarer til det nye driftsniveau.
I realiteten nulstiller den integrale virkning kontinuerligt bias-værdien for at eliminere forskydning, når driftsniveauet ændres.
Udfordringer ved PI-regulering
Der er udfordringer ved at anvende PI-algoritmen:
| ▪ | De to indstillings parametre interagerer med hinanden, og deres indflydelse skal afbalanceres af konstruktøren. |
| ▪ | Den integrale term har en tendens til at øge den oscillerende eller rullende adfærd i procesresponsen. |
Da de to tuningparametre interagerer med hinanden, kan det være en udfordring at nå frem til de “bedste” tuningværdier. Værdien og vigtigheden af vores design- og indstillingsopskrift øges, efterhånden som regulatoren bliver mere kompleks.
Initialisering af regulatoren til bumpløs overførsel
Når vi skifter en hvilken som helst regulator fra manuel tilstand til automatisk tilstand (fra åben sløjfe til lukket sløjfe), ønsker vi, at resultatet skal være begivenhedsløst. Det vil sige, at vi ikke ønsker, at overgangen skal forårsage pludselige reguleringshandlinger, der påvirker eller forstyrrer vores proces
Vi opnår dette ønskede resultat ved overgangen ved at initialisere regulators integralfejlsummen til nul. Desuden initialiseres setpunktet og reguleringsbiasværdien ved at indstille:
▪ SP lig med den aktuelle PV
▪ CObias lig med den aktuelle CO
Med fejlintegralsummen sat til nul er der intet at tilføje eller trække fra CObias, som ville forårsage en pludselig ændring i den aktuelle reguleringsudgang. Når setpunktet er lig med den målte procesvariabel, er der ingen fejl, der kan medføre en ændring i vores CO Og med reguleringsbiaset indstillet til vores aktuelle CO-værdi er vi som standard forberedt på at opretholde den aktuelle drift.
Så når vi skifter fra manuel tilstand til automatisk tilstand, har vi “bumpless transfer” uden overraskelser. Dette er et resultat, som alle sætter pris på.
Reset Time Versus Reset Rate
De forskellige leverandører støber deres kontrolalgoritmer i lidt forskellige former. Nogle bruger proportionalbånd i stedet for reguleringsforstærkning. Nogle bruger også nulstillingshastighed, Tr, i stedet for nulstillingstid. Disse er simpelthen den inverse af hinanden:
Tr = 1/Ti
Og uanset hvordan tuningsparametrene udtrykkes, er PI-algoritmerne alle lige dygtige.
Men det er afgørende at kende sin producent, før man begynder at indstille sin regulator, fordi parameterværdierne skal tilpasses til den pågældende algoritmeform.Kommerciel software til reguleringsdesign og tuning vil automatisk løse dette problem for dig.
Implementering af en PI-regulator
Vi udforsker PI-regulatorens design, tuning og implementering på varmeveksleren i denne artikel og de tyngdekraftdrænede tanke i denne artikel.