Eulers identitet virker forvirrende:
![]()
Det fremgår af en mere generel formel:
![]()
Yowza — vi relaterer en imaginær eksponent til sinus og cosinus! Og på en eller anden måde giver indsættelse af pi -1? Kan det nogensinde være intuitivt?
Det er ikke ifølge 1800-tallets matematiker Benjamin Peirce:
Det er absolut paradoksalt; vi kan ikke forstå det, og vi ved ikke, hvad det betyder, men vi har bevist det, og derfor ved vi, at det må være sandheden.
Argh, denne holdning får mit blod til at koge! Formler er ikke magiske besværgelser, som man kan lære udenad: Vi må, må, må, må finde en indsigt. Her er min:
Eulers formel beskriver to ækvivalente måder at bevæge sig i en cirkel på.
Er det alt? Denne fantastiske ligning handler om at dreje rundt? Ja – og vi kan forstå den ved at bygge på et par analogier:
- Gå ud fra tallet 1 og se multiplikation som en transformation, der ændrer tallet: $1 \cdot e^{i \pi}$$
- Regulær eksponentiel vækst øger kontinuerligt 1 med en vis hastighed i en vis tidsperiode; imaginær eksponentiel vækst roterer kontinuerligt 1 i en vis tidsperiode
- Vækst i “pi” tidsenheder betyder at gå pi radianer rundt om en cirkel
- Derfor betyder $e^{i \pi}$ at starte ved 1 og rotere pi (halvvejs rundt om en cirkel) for at komme til -1
Det er det overordnede synspunkt, lad os dykke ned i detaljerne. I øvrigt, hvis nogen forsøger at imponere dig med $e^{i \pi} = -1$, så spørg dem om i til den i-te potens. Hvis de ikke kan tænke det igennem, er Eulers formel stadig en trylleformular for dem.
Opdatering: Mens jeg skrev, tænkte jeg, at en video måske kunne hjælpe med at forklare ideerne mere klart:
Forstå cos(x) + i * sin(x)
Gligningstegnet er overbelastet. Nogle gange mener vi “sætter en ting til en anden” (som x = 3), og andre gange mener vi “disse to ting beskriver det samme begreb” (som $\sqrt{-1} = i$).
Eulers formel er sidstnævnte: den giver to formler, der forklarer, hvordan man bevæger sig i en cirkel. Hvis vi undersøger cirkelbevægelse ved hjælp af trigonometri og bevæger os x radianer:
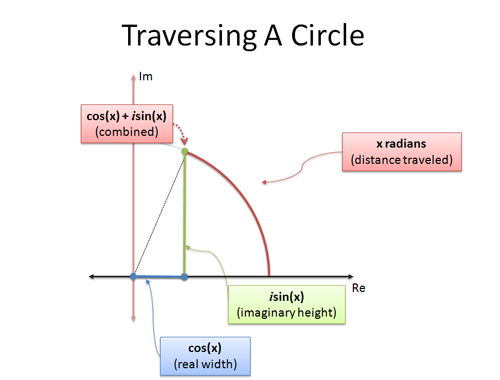
- cos(x) er x-koordinaten (vandret afstand)
- sin(x) er y-koordinaten (lodret afstand)
Sætningen
![]()
er en smart måde at smide x- og y-koordinaterne sammen til et enkelt tal. Analogien “komplekse tal er 2-dimensionelle” hjælper os med at fortolke et enkelt komplekst tal som en position på en cirkel.
Når vi sætter x til $\pi$, bevæger vi os $\pi$ enheder langs ydersiden af enhedscirklen. Da den samlede omkreds er $2\pi$, er almindelig $\pi$ halvvejs rundt, hvilket bringer os til -1.
Neato: Den højre side af Eulers formel ($\cos(x) + i \sin(x)$) beskriver cirkulær bevægelse med imaginære tal. Lad os nu finde ud af, hvordan e-siden af ligningen opnår det.
Hvad er imaginær vækst?
At kombinere x- og y-koordinater til et komplekst tal er tricky, men håndterbart. Men hvad betyder en imaginær eksponent?
Lad os træde lidt tilbage. Når jeg ser $3^4$, tænker jeg på det sådan her:
- 3 er slutresultatet af at vokse øjeblikkeligt (ved hjælp af e) med en hastighed på ln(3). Med andre ord: $3 = e^{\ln(3)}$$
- $3^4$ er det samme som at vokse til 3, men så vokse i 4x så lang tid. Så $3^4 = e^{\ln(3) \cdot 4} = 81$
I stedet for at se tallene i sig selv, kan man tænke på dem som noget, e skulle “vokse til”. Reelle tal, som 3, giver en rente på ln(3) = 1,1, og det er det, som e “samler” op, mens det går fremad og vokser kontinuerligt.
Regulær vækst er enkel: den bliver ved med at “skubbe” et tal i den samme, reelle retning, som det var på vej hen. 3 × 3 skubber i den oprindelige retning og gør det 3 gange større (9).
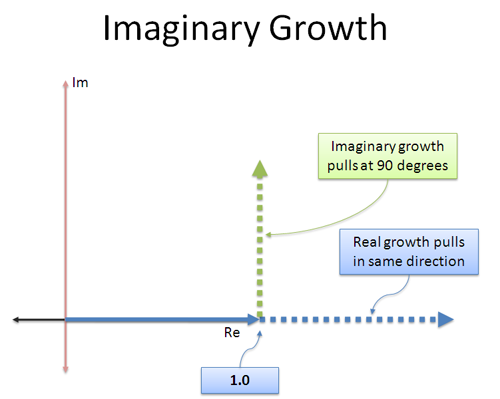
Imaginær vækst er anderledes: De “renter”, vi tjener, går i en anden retning! Det er ligesom en jetmotor, der blev spændt fast sidelæns – i stedet for at køre fremad, begynder vi at skubbe 90 grader.
Det smarte ved et konstant ortogonalt (vinkelret) skub er, at det ikke sætter fart på dig eller bremser dig – det roterer dig! Hvis man tager et hvilket som helst tal og multiplicerer det med i, ændrer det ikke størrelsen, men blot den retning det peger i.
Intuitivt er det sådan her, jeg ser den konstante imaginære vækstrate: “Når jeg vokser, skal du ikke skubbe mig frem eller tilbage i den retning, jeg allerede er på vej. Drej mig i stedet.”
Men burde vi ikke snurre hurtigere og hurtigere?
Det undrede jeg mig også over. Regelmæssig vækst sammensætter sig i vores oprindelige retning, så vi går 1, 2, 4, 8, 16, multiplicerer 2x hver gang og bliver i de reelle tal. Vi kan betragte dette som $e^{\ln(2)x}$$, hvilket betyder at vokse øjeblikkeligt med en hastighed på ln(2) i “x” sekunder.
Og hey — hvis vores vækstrate var dobbelt så hurtig, 2ln(2) vs. ln(2), ville det se det samme ud som at vokse i dobbelt så lang tid (2x vs. x). Magien i e lader os bytte om på hastighed og tid; 2 sekunder ved ln(2) er den samme vækst som 1 sekund ved 2ln(2).
Nu forestiller vi os, at vi har en eller anden rent imaginær vækstrate (Ri), der roterer os, indtil vi når i, eller 90 grader opad. Hvad sker der, hvis vi fordobler denne hastighed til 2Ri, vil vi så dreje ud af cirklen?
Nej! At have en hastighed på 2Ri betyder, at vi bare drejer dobbelt så hurtigt, eller alternativt drejer vi med en hastighed på R i dobbelt så lang tid, men vi bliver på cirklen. At rotere dobbelt så længe betyder, at vi nu vender 180 grader.
Når vi indser, at en eller anden eksponentiel væksthastighed kan føre os fra 1 til i, vil en forøgelse af denne hastighed blot dreje os mere rundt. Vi slipper aldrig ud af cirklen.
Men hvis vores vækstrate er kompleks (a+bi vs Ri), så vil den reelle del (a) vokse os som normalt, mens den imaginære del (bi) roterer os. Men lad os nu ikke blive for fine: Eulers formel, $e^{ix}$, handler om den rent imaginære vækst, der holder os på cirklen (mere senere).
Et hurtigt sanitetstjek
Mens jeg skrev, måtte jeg afklare et par spørgsmål for mig selv:
Hvorfor bruge $e^x$, roterer vi ikke tallet 1?
e repræsenterer processen med at starte ved 1 og vokse kontinuerligt med 100 % rente i 1 tidsenhed.
Når vi skriver e, fanger vi hele denne proces i et enkelt tal — e repræsenterer hele den kontinuerlige væksts rigmaroller. Så i virkeligheden siger $e^x$ “start ved 1 og voks kontinuerligt med 100 % i x sekunder”, og starter fra 1, som vi ønsker det.
Men hvad gør i som eksponent?
For en almindelig eksponent som $3^4$ spørger vi:
- Hvad er den implicitte vækstrate? Vi vokser fra 1 til 3 (eksponentens base).
- Hvordan ændrer vi denne vækstrate? Vi skalerer den med 4x (potensen af eksponenten).
Vi kan konvertere vores vækst til “e”-format: Vores øjeblikkelige vækstrate er ln(3), og vi øger den til ln(3) * 4. Igen har potensen af eksponenten (4) netop skaleret vores vækstrate.
![]()
Når den øverste eksponent er i (som i $3^i$), multiplicerer vi bare vores implicitte vækstrate med i. Så i stedet for at vokse med almindelig gammel ln(3) vokser vi med ln(3) * i.
![]()
Den øverste del af eksponenten ændrer den implicitte vækstrate i den nederste del.
De små detaljer
Lad os se nærmere på det. Husk denne definition af e:
![]()
Det $\frac{100\%}{n}$ repræsenterer den del af renten, som vi har tjent i hver mikroskopisk periode. Vi antog, at renten var 100 % i den reelle dimension — men hvad nu, hvis den var 100 % i den imaginære retning?
![]()
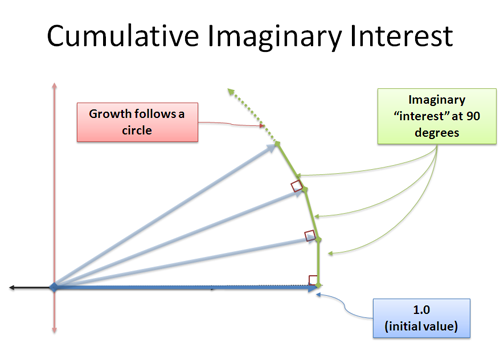
Nu tilføjer vores nyoprettede rente os i 90-graders retning. Overraskende nok ændrer det ikke vores længde – det er et tricky begreb, for det ser ud til at lave en trekant, hvor hypotenusen skal være større. Vi har med en grænse at gøre, og den ekstra afstand ligger inden for den fejlmargin, vi angiver. Dette er noget, jeg vil tage fat på en anden dag, men tag mit ord på ordet: kontinuerlig vinkelret vækst vil rotere dig. Dette er kernen i sinus og cosinus, hvor din ændring er vinkelret på din nuværende position, og du bevæger dig i en cirkel.
Vi anvender i enheder af vækst i uendeligt små trin, der hver især skubber os i en 90 graders vinkel. Der er ingen “hurtigere og hurtigere” rotation – i stedet kravler vi langs omkredsen en strækning på |i| = 1 (størrelsen af i).
Og hey — den strækning, man kravler rundt om en cirkel, er en vinkel i radianer! Vi har fundet en anden måde at beskrive cirkulær bevægelse på!
For at få cirkulær bevægelse: Ændre kontinuerligt ved at dreje i en vinkel på 90 grader (aka imaginær vækstrate).
Så, Eulers formel siger “eksponentiel, imaginær vækst tegner en cirkel”. Og denne bane er det samme som at bevæge sig i en cirkel ved hjælp af sinus og cosinus i det imaginære plan.
I dette tilfælde er ordet “eksponentiel” forvirrende, fordi vi bevæger os rundt i en cirkel med en konstant hastighed. I de fleste diskussioner antages det, at eksponentiel vækst har en kumulativ, sammensat virkning.
Nogle eksempler
Du tror mig ikke rigtig, vel? Her er et par eksempler, og hvordan man intuitivt kan tænke over dem.
Eksempel: $e^i$
Hvor er x’et? Ah, det er bare 1. Intuitivt, uden at skulle finde en lommeregner frem, ved vi, at det betyder “rejse 1 radian langs enhedscirklen”. I mit hoved ser jeg, at “e” forsøger at vokse 1 på 100% alle i samme retning, men i bliver ved med at flytte kuglen og tvinger “1” til at vokse langs kanten af en cirkel:
![]()
Det er ikke det kønneste tal, men der er det. Husk at sætte din lommeregner i radiantilstand, når du stempler dette ind.
Eksempel: $3^i$
Dette er tricky — det er ikke i vores standardformat. Men husk, ![]()
Vi ønsker en initial vækst på 3x i slutningen af perioden, eller en øjeblikkelig hastighed på ln(3). Men, i’et kommer til og ændrer denne hastighed af ln(3) til “i * ln(3)”:
![]()
Vi troede, at vi ville transformere med en regelmæssig hastighed af ln(3), lidt hurtigere end 100 % kontinuerlig vækst, da e er ca. 2,718. Men åh nej, jeg snurrede os rundt: nu transformerer vi med en imaginær hastighed, hvilket betyder at vi bare roterer rundt. Hvis i var et regulært tal som 4, ville det have fået os til at vokse 4x hurtigere. Nu vokser vi med en hastighed på ln(3), men sidelæns.
Vi burde forvente et komplekst tal på enhedscirklen — der er intet i vækstraten, der øger vores størrelse. Løsning af ligningen:
![]()
Så i stedet for at ende “1” enhed rundt om cirklen (som $e^i$) ender vi ln(3) enheder rundt.
Eksempel: $i^i$
For et par måneder siden ville dette have fået mig til at græde. Ikke i dag! Lad os bryde transformationerne ned:
![]()
Vi starter med 1 og ønsker at ændre det. Ligesom ved at løse $3^i$, hvad er den øjeblikkelige vækstrate repræsenteret ved i som base?
Hrm. Normalt ville vi lave ln(x) for at få den vækstrate, der skal til for at nå x ved udgangen af 1 tidsenhed. Men for en imaginær hastighed? Vi er nødt til at nørkle med det her.
For at starte med 1 og vokse til i er vi nødt til at begynde at rotere fra starten. Hvor hurtigt? Jo, vi skal nå 90 grader (pi/2 radianer) på 1 tidsenhed. Så vores hastighed er $i \frac{\pi}{2}$. Husk, at vores hastighed skal være imaginær, da vi roterer, ikke vokser! Almindelig $\frac{\pi}{2}$ er ca. 1,57 og resulterer i regelmæssig vækst.
Dette burde give mening: for at vende 1,0 til i i i slutningen af 1 enhed skal vi rotere $\frac{\pi}{2}$ radianer (90 grader) i den mængde tid. Så for at få “i” kan vi bruge $e^{i \frac{\pi}{2}}}$.
![]()
Phew. Det beskriver i som basis. Hvad med eksponenten?
Jamen, det andet i fortæller os, at vi skal ændre vores sats — ja, den sats, vi brugte så lang tid på at regne ud! Så i stedet for at rotere med en hastighed på $i \frac{\pi}{2}$, hvilket er det, som en base på i betyder, omdanner vi hastigheden til:
![]()
Den i’er ophæver hinanden og gør vækstraten reel igen! Vi roterede vores rate og skubbede os ind i de negative tal. Og en negativ vækstrate betyder, at vi skrumper – vi bør forvente, at $i^i$ gør tingene mindre. Og det gør det:
![]()
Tada! (Søg på “i^i” på Google for at bruge dens beregner)
Tag en dyb indånding: Du kan intuitivt regne ud, hvordan imaginære baser og imaginære eksponenter skal opføre sig. Whoa.
Og som en bonus har du regnet ln(i) ud – for at få $e^x$ til at blive i, skal du få e til at rotere $\frac{\pi}{2}$ radianer.
![]()
Eksempel: (i^i)^i
En dobbelt imaginær eksponent? Hvis du insisterer. For det første ved vi, hvad vores vækstrate vil være inden for parentesen:
![]()
Vi får en negativ (krympende) vækstrate på -pi/2. Og nu modificerer vi denne hastighed igen med i:
![]()
Og nu har vi en negativ rotation! Vi går rundt i cirklen med en hastighed på $-\frac{\pi}{2}$ pr. tidsenhed. Hvor lang tid skal vi gå i? Tja, der er en implicit “1” tidsenhed helt i toppen af denne eksponentkæde; den implicitte standard er at gå i 1 tidsenhed (ligesom $e = e^1$). 1 tidsenhed giver os en rotation på $-\frac{\pi}{2}$ radianer (-90 grader) eller -i!
![]()
Og, bare for sjov, hvis vi kvadrerede dette vanvittige resultat:
Det er “bare” den dobbelte rotation: 2 er et regulært tal, så det fordobler vores rotationshastighed til hele -180 grader i en tidsenhed. Eller man kan se på det som at anvende -90 graders rotation to gange i træk.
Op det første øjekast er det virkelig mærkelige eksponenter. Men med vores analogier kan vi tage dem med ro.
Kompleks vækst
Vi kan have reel og imaginær vækst på samme tid: Den reelle del skalerer os op, og den imaginære del roterer os rundt:
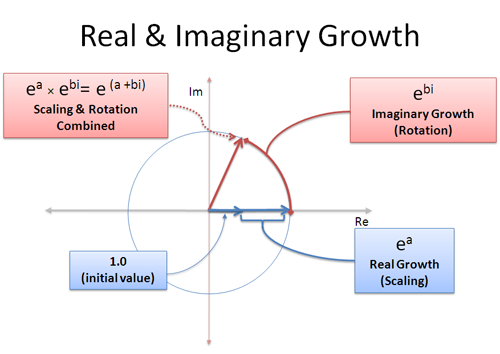
En kompleks vækstrate som (a + bi) er en blanding af reel og imaginær vækst. Den reelle del a, betyder “vokse med 100 % i a sekunder”, og den imaginære del b betyder “rotere i b sekunder”. Husk, at rotationer ikke får fordelene ved sammensætning, da du bliver ved med at “skubbe” i en anden retning – rotationer summerer lineært.
Med dette i baghovedet kan vi repræsentere ethvert punkt på en cirkel af enhver størrelse ved hjælp af (a+bi)! Radius er $e^a$ og vinklen er bestemt af $e^{bi}$. Det svarer til at sætte tallet i expand-o-tron i to cyklusser: en gang for at vokse det til den rigtige størrelse (a sekunder), en anden gang for at rotere det til den rigtige vinkel (b sekunder). Eller man kunne rotere det først og så vokse!
Lad os sige, at vi ønsker at kende vækstbeløbet for at komme til 6 + 8i. Det er i virkeligheden et spørgsmål om den naturlige logaritme af et imaginært tal: Hvordan vokser vi e for at få (6 + 8i)?
- Radius: Hvor stor en cirkel har vi brug for? Tja, størrelsen er $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Det betyder, at vi skal vokse i ln(10) = 2,3 sekunder for at nå dette beløb.
- Mængde til at rotere: Hvad er vinklen på dette punkt? Vi kan bruge arctan til at finde ud af det: atan(8/6) = 53 grader = .93 radian.
- Kombinér resultatet: ln(6+8i) = 2,3 + .93i
Det vil sige, at vi kan nå det tilfældige punkt (6 + 8i), hvis vi bruger $e^{2.3 + .93i}$.
Hvorfor er det nyttigt?
Eulers formel giver os en anden måde at beskrive bevægelse i en cirkel på. Men det kan vi allerede gøre med sinus og cosinus – hvad er så specielt?
Det hele handler om perspektiv. Sinus og cosinus beskriver bevægelsen i form af et gitter, hvor man plotter horisontale og vertikale koordinater ud.

Eulers formel bruger polære koordinater — hvad er din vinkel og afstand? Igen, det er to måder at beskrive bevægelse på:
- Grid-system: Gå 3 enheder mod øst og 4 enheder mod nord
- Polarkoordinater: Gå 5 enheder i en vinkel på 53,13 grader
Afhængigt af problemet er polære eller rektangulære koordinater mere anvendelige. Med Eulers formel kan vi konvertere mellem de to for at bruge det bedste værktøj til opgaven. Da $e^{ix}$ kan omregnes til sinus og cosinus, kan vi også omskrive formler i trigonometri som variationer af e, hvilket er meget praktisk (du behøver ikke at huske sin(a+b), du kan udlede det – mere en anden dag). Og det er smukt, at ethvert tal, reelt eller komplekst, er en variation af e.
Men nytte, schmutility: det vigtigste resultat er erkendelsen af, at forvirrende ligninger kan blive intuitive med de rigtige analogier. Lad ikke smukke ligninger som Eulers formel forblive en trylleformular – byg på de analogier, du kender, for at se indsigten inde i ligningen.
Happy math.
Appendix
Screencastet var sjovt, og feedback er bestemt velkommen. Jeg synes, det hjælper ideerne til at poppe op, og at gå gennem artiklen hjalp mig med at finde huller i min intuition.
- Brian Slesinsky har en pæn præsentation om Eulers formel
- Visual Complex Analysis har en god diskussion om Eulers formel — se s. 10 i Google Book Preview
- Jeg lavede et foredrag om Math and Analogies, som forklarer Eulers identitet mere visuelt:
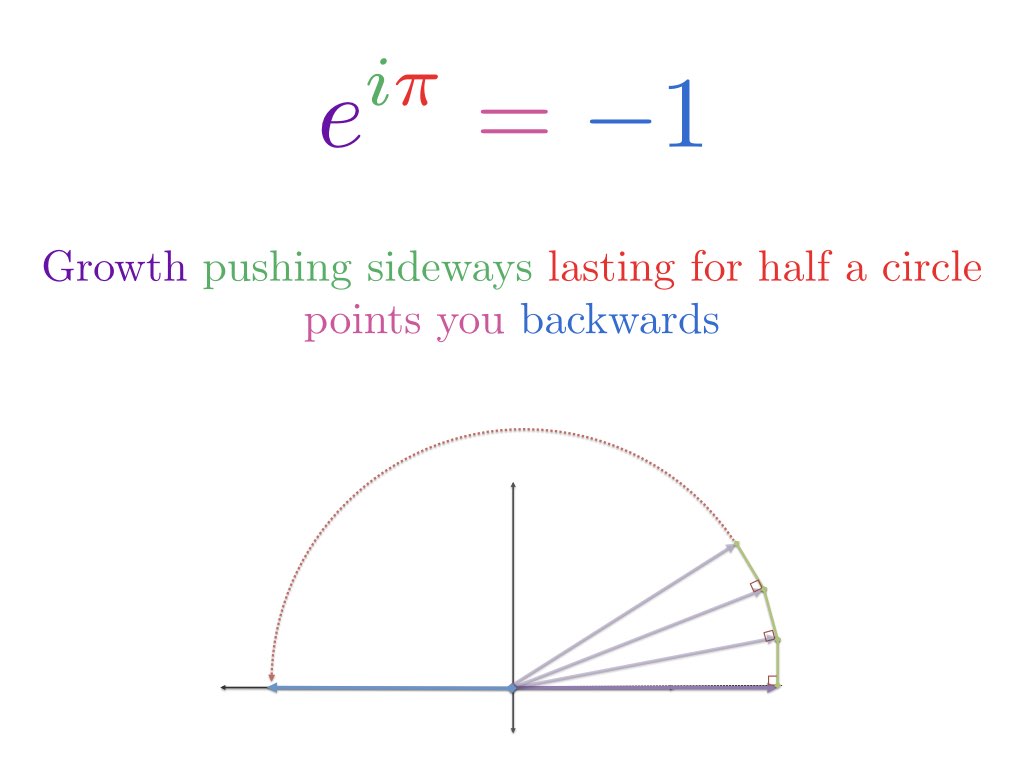
Andre indlæg i denne serie
- En visuel, intuitiv guide til imaginære tal
- Intuitiv aritmetik med komplekse tal
- Forstå, hvorfor kompleks multiplikation virker
- Intuitiv guide til vinkler, Grader og radianer
- Intuitiv forståelse af Eulers formel
- Interaktiv vejledning i Fouriertransformationen
- Intuitiv vejledning i konvolution
- Intuitiv forståelse af sinusbølger
- En intuitiv vejledning i lineær algebra
- En programmørens intuition for matrixmultiplikation
- Imaginær multiplikation vs. Imaginære eksponenter