Lernziele
- Die Beziehung zwischen der Stärke einer Säure oder Base und der Größe von \(K_a\), \(K_b\), \(pK_a\) und \(pK_b\) kennen.
- Um den Nivellierungseffekt zu verstehen.
Die Größe der Gleichgewichtskonstante für eine Ionisierungsreaktion kann zur Bestimmung der relativen Stärke von Säuren und Basen verwendet werden. Zum Beispiel lautet die allgemeine Gleichung für die Ionisierung einer schwachen Säure in Wasser, wobei HA die Ausgangssäure und A- ihre konjugierte Base ist, wie folgt:
\
Die Gleichgewichtskonstante für diese Dissoziation lautet wie folgt:
\}{}
Wie wir bereits festgestellt haben, ist die Wasserkonzentration für alle Reaktionen in wässriger Lösung im Wesentlichen konstant, so dass \(\) in Gleichung \(\ref{16.5.2}\) in eine neue Größe, die Säureionisationskonstante (\(K_a\)), die auch als Säuredissoziationskonstante bezeichnet wird, integriert werden kann:
\=\dfrac{}{}
Die Zahlenwerte von K und \(K_a\) unterscheiden sich also durch die Konzentration des Wassers (55,3 M). Der Einfachheit halber kann \(H_3O^+\) auch als \(H^+\) in Gleichung \(\ref{16.5.3}\) geschrieben werden. Es ist jedoch zu beachten, dass freies \(H^+\) in wässrigen Lösungen nicht existiert und dass bei allen Säureionisierungsreaktionen ein Proton auf \(H_2O\) übertragen wird, um Hydroniumionen, \(H_3O^+\), zu bilden. Je größer \(K_a\) ist, desto stärker ist die Säure und desto höher ist die \(H^+\)-Konzentration im Gleichgewichtszustand. Wie alle Gleichgewichtskonstanten werden auch die Säure-Base-Ionisationskonstanten in Bezug auf die Aktivitäten von \(H^+\) oder \(OH^-\) gemessen und sind somit einheitenlos. Die Werte von \(K_a\) für eine Reihe gängiger Säuren sind in Tabelle \(\PageIndex{1}\) angegeben.
Schwache Basen reagieren mit Wasser unter Bildung des Hydroxidions, wie in der folgenden allgemeinen Gleichung dargestellt, wobei B die Ausgangsbase und BH+ ihre konjugierte Säure ist:
\
Die Gleichgewichtskonstante für diese Reaktion ist die Basen-Ionisationskonstante (Kb), die auch als Basendissoziationskonstante bezeichnet wird:
\= \frac{}{}
Auch hier ist die Wasserkonzentration konstant, so dass sie nicht im Ausdruck für die Gleichgewichtskonstante erscheint; stattdessen ist sie in \(K_b\) enthalten. Je größer der \(K_b\) ist, desto stärker ist die Base und desto höher ist die \(OH^-\)-Konzentration im Gleichgewicht. Die Werte von \(K_b\) für eine Reihe gebräuchlicher schwacher Basen sind in Tabelle \(\PageIndex{2}\) angegeben.
Es gibt eine einfache Beziehung zwischen der Größe von \(K_a\) für eine Säure und \(K_b\) für ihre konjugierte Base. Betrachten wir zum Beispiel die Ionisierung von Blausäure (\(HCN\)) in Wasser, um eine saure Lösung zu erzeugen, und die Reaktion von \(CN^-\) mit Wasser, um eine basische Lösung zu erzeugen:
\
\
Der Ausdruck der Gleichgewichtskonstante für die Ionisierung von HCN lautet wie folgt:
\}{}
Der entsprechende Ausdruck für die Reaktion von Cyanid mit Wasser lautet wie folgt:
\}{} \label{16.5.9}\]
Wenn wir die Gleichungen \(\ref{16.5.6}\) und \(\ref{16.5.7}\), erhalten wir folgendes:
| Reaktion | Gleichgewichtskonstanten |
|---|---|
| \(\cancel{HCN_{(aq)}} \rightleftharpoons H^+_{(aq)}+\cancel{CN^-_{(aq)}} \) | \(K_a=\cancel{}/\cancel{}\) |
| \(\cancel{CN^-_{(aq)}}+H_2O_{(l)} \rightleftharpoons OH^-_{(aq)}+\cancel{HCN_{(aq)}}) | \(K_b=\cancel{}/\cancel{}\) |
| \(H_2O_{(l)} \rightleftharpoons H^+_{(aq)}+OH^-_{(aq)}\) | \(K=K_a \times K_b=\) |
In diesem Fall, ist die Summe der durch \(K_a\) und \(K_b\) beschriebenen Reaktionen die Gleichung für die Autoionisation von Wasser, und das Produkt der beiden Gleichgewichtskonstanten ist \(K_w\):
\
Wenn wir also entweder \(K_a\) für eine Säure oder \(K_b\) für ihre konjugierte Base kennen, können wir die andere Gleichgewichtskonstante für jedes konjugierte Säure-Base-Paar berechnen.
Genauso wie bei \(pH\), \(pOH\) und pKw können wir negative Logarithmen verwenden, um die Exponentialschreibweise beim Schreiben von Säure- und Basen-Ionisationskonstanten zu vermeiden, indem wir \(pK_a\) wie folgt definieren:
\
\
und \(pK_b\) als
\
Ähnlich ist die Gleichung \(\ref{16.5.10}\), die die Beziehung zwischen \(K_a\) und \(K_b\) ausdrückt, kann in logarithmischer Form wie folgt geschrieben werden:
\
Bei 25 °C wird daraus
\
Die Werte von \(pK_a\) und \(pK_b\) sind für mehrere gängige Säuren und Basen in den Tabellen \(\PageIndex{1}\) und \(\PageIndex{2}\) angegeben, aufgeführt, und die Tabellen E1 und E2 enthalten einen umfangreicheren Satz von Daten. Aufgrund der Verwendung negativer Logarithmen entsprechen kleinere Werte von \(pK_a\) größeren Säureionisationskonstanten und damit stärkeren Säuren. Zum Beispiel ist salpetrige Säure (\(HNO_2\)) mit einem \(pK_a\) von 3,25 etwa eine Million Mal stärker als Blausäure (HCN) mit einem \(pK_a\) von 9,21. Umgekehrt entsprechen kleinere Werte von \(pK_b\) größeren Basen-Ionisationskonstanten und damit stärkeren Basen.
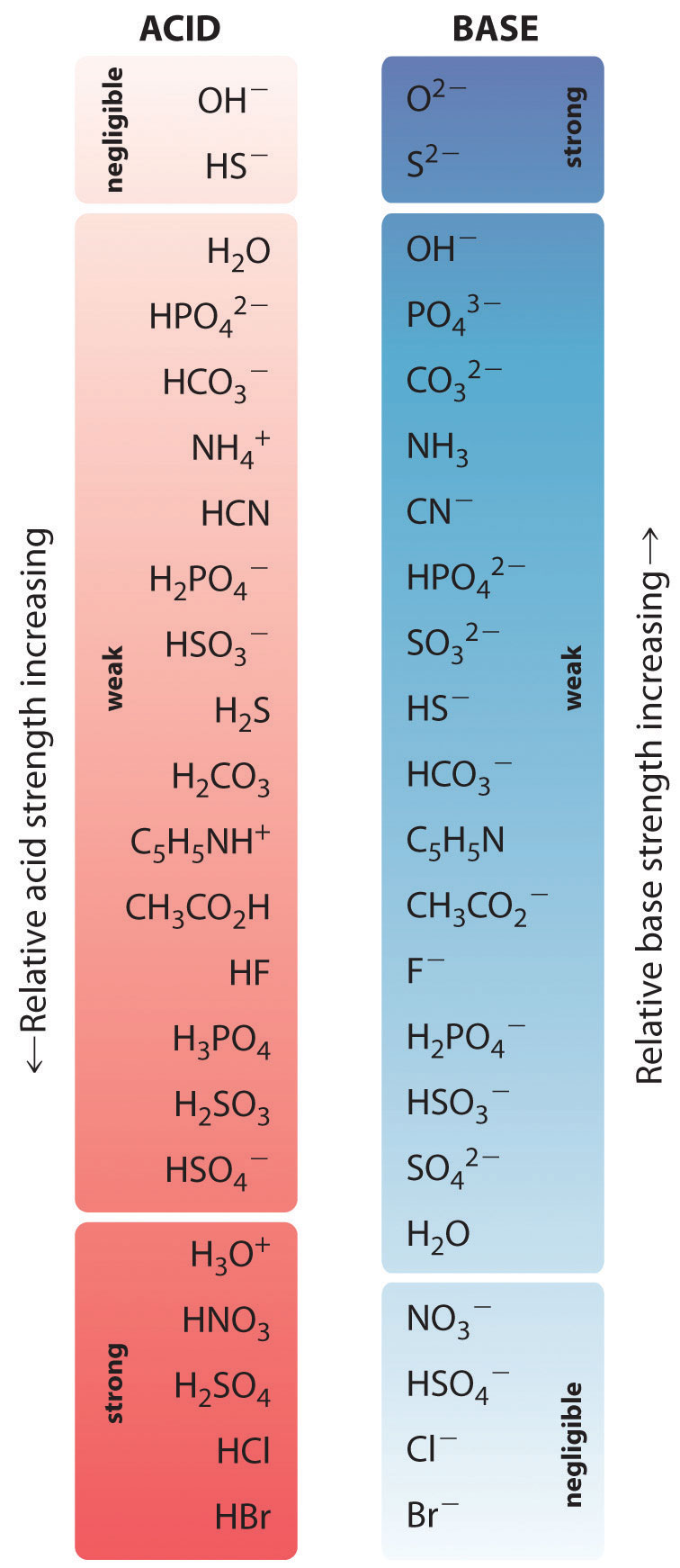
Die relativen Stärken einiger gebräuchlicher Säuren und ihrer konjugierten Basen sind in Abbildung \(\PageIndex{1}\) grafisch dargestellt. Die konjugierten Säure-Base-Paare sind in der Reihenfolge (von oben nach unten) zunehmender Säurestärke aufgelistet, die abnehmenden Werten von \(pK_a\) entspricht. Diese Reihenfolge entspricht einer abnehmenden Stärke der konjugierten Base oder steigenden Werten von \(pK_b\). Unten links in der Abbildung \(\PageIndex{2}\) befinden sich die häufigsten starken Säuren, oben rechts die häufigsten starken Basen. Beachten Sie die umgekehrte Beziehung zwischen der Stärke der Ausgangssäure und der Stärke der konjugierten Base. So ist die konjugierte Base einer starken Säure eine sehr schwache Base, und die konjugierte Base einer sehr schwachen Säure ist eine starke Base.
Die konjugierte Base einer starken Säure ist eine schwache Base und umgekehrt.
Wir können die relativen Stärken von Säuren und Basen verwenden, um die Richtung einer Säure-Base-Reaktion vorherzusagen, indem wir eine einzige Regel befolgen: Ein Säure-Base-Gleichgewicht begünstigt immer die Seite mit der schwächeren Säure und Base, wie durch diese Pfeile angedeutet:
\
In einer Säure-Base-Reaktion reagiert das Proton immer mit der stärkeren Base.
Zum Beispiel ist Salzsäure eine starke Säure, die in verdünnter wässriger Lösung im Wesentlichen vollständig ionisiert, wobei \(H_3O^+\) und \(Cl^-\) entstehen; nur vernachlässigbare Mengen von \(HCl\)-Molekülen bleiben undissoziiert. Daher liegt das Ionisierungsgleichgewicht praktisch ganz rechts, wie durch einen einzelnen Pfeil dargestellt:
\
Im Gegensatz dazu ist Essigsäure eine schwache Säure und Wasser eine schwache Base. Folglich enthalten wässrige Lösungen von Essigsäure hauptsächlich Essigsäuremoleküle im Gleichgewicht mit einer geringen Konzentration von \(H_3O^+\) und Acetat-Ionen, und das Ionisierungsgleichgewicht liegt weit links, wie durch diese Pfeile dargestellt:
\
In ähnlicher Weise ist bei der Reaktion von Ammoniak mit Wasser das Hydroxid-Ion eine starke Base und Ammoniak eine schwache Base, während das Ammonium-Ion eine stärkere Säure als Wasser ist. Daher liegt auch dieses Gleichgewicht links:
\
Alle Säure-Base-Gleichgewichte begünstigen die Seite mit der schwächeren Säure und Base. So wird das Proton an die stärkere Base gebunden.
Beispiel \(\PageIndex{1}\): Butyrat- und Dimethylammonium-Ionen
- Berechnen Sie \(K_b\) und \(pK_b\) des Butyrat-Ions (\(CH_3CH_2CH_2CO_2^-\)). Der \(pK_a\) von Buttersäure bei 25°C beträgt 4,83. Buttersäure ist für den üblen Geruch von ranziger Butter verantwortlich.
- Berechnen Sie \(K_a\) und \(pK_a\) des Dimethylammonium-Ions (\((CH_3)_2NH_2^+\)). Die Basen-Ionisationskonstante \(K_b\) von Dimethylamin (\((CH_3)_2NH\)) ist \(5,4 \mal 10^{-4}\) bei 25°C.
Gibt: \(pK_a\) und \(K_b\)
Gefragt: entsprechende \(K_b\) und \(pK_b\), \(K_a\) und \(pK_a\)
Strategie:
Die Konstanten \(K_a\) und \(K_b\) sind wie in Gleichung \(\ref{16.5.10}\). Die Konstanten \(pK_a\) und \(pK_b\) für eine Säure und ihre konjugierte Base sind in den Gleichungen \(\ref{16.5.15}\) und \(\ref{16.5.16}\) dargestellt. Verwenden Sie die Beziehungen pK = -log K und K = 10-pK (Gleichungen \(\ref{16.5.11}\) und \(\ref{16.5.13}\)), um zwischen \(K_a\) und \(pK_a\) oder \(K_b\) und \(pK_b\) umzurechnen.
Lösung:
Wir erhalten den \(pK_a\) für Buttersäure und sollen den \(K_b\) und den \(pK_b\) für ihre konjugierte Base, das Butyrat-Ion, berechnen. Da der angegebene \(pK_a\)-Wert für eine Temperatur von 25 °C gilt, können wir die Gleichung \(\ref{16.5.16}\) verwenden: \(pK_a\) + \(pK_b\) = pKw = 14,00. Durch Substitution von \(pK_a\) und Lösung von \(pK_b\),
\
\
Da \(pK_b = -\log K_b\), ist \(K_b\) \(10^{-9.17} = 6.8 \mal 10^{-10}\).
In diesem Fall ist \(K_b\) für eine Base (Dimethylamin) gegeben und wir sollen \(K_a\) und \(pK_a\) für ihre konjugierte Säure, das Dimethylammoniumion, berechnen. Da die angegebene Ausgangsgröße \(K_b\) und nicht \(pK_b\) ist, können wir die Gleichung \(\ref{16.5.10}\) verwenden: \(K_aK_b = K_w\). Wenn man die Werte von \(K_b\) und \(K_w\) bei 25°C einsetzt und nach \(K_a\) löst,
\
\
Da \(pK_a\) = -log \(K_a\) ist, haben wir \(pK_a = -\log(1,9 \mal 10^{-11}) = 10,72\). Wir hätten auch \(K_b\) in \(pK_b\) umwandeln können, um die gleiche Antwort zu erhalten:
\
\
\
\
Wenn wir eine dieser vier Größen für eine Säure oder eine Base erhalten (\(K_a\), \(pK_a\), \(K_b\) oder \(pK_b\)), können wir die anderen drei berechnen.
Übung \(\PageIndex{1}\): Milchsäure
Milchsäure (\(CH_3CH(OH)CO_2H\)) ist für den scharfen Geschmack und Geruch von Sauermilch verantwortlich; es wird auch vermutet, dass sie Muskelkater in ermüdeten Muskeln verursacht. Sein \(pK_a\) beträgt 3,86 bei 25°C. Berechnen Sie \(K_a\) für Milchsäure und \(pK_b\) und \(K_b\) für das Laktat-Ion.
Antwort
- \(K_a = 1,4 \mal 10^{-4}\) für Milchsäure;
- \(pK_b\) = 10.14 und
- \(K_b = 7,2 \times 10^{-11}\) für das Laktat-Ion
Lösungen starker Säuren und Basen: Der Nivellierungseffekt
Sie werden in der Tabelle \(\PageIndex{1}\) feststellen, dass Säuren wie \(H_2SO_4\) und \(HNO_3\) über dem Hydronium-Ion liegen, was bedeutet, dass sie \(pK_a\)-Werte kleiner als Null haben und stärkere Säuren sind als das \(H_3O^+\)-Ion. Aus Kapitel 4 wissen wir, dass das saure Proton in praktisch allen Oxosäuren an eines der Sauerstoffatome des Oxoanions gebunden ist. Daher sollte Salpetersäure korrekt als \(HONO_2\) geschrieben werden. Leider werden die Formeln von Oxosäuren jedoch fast immer mit Wasserstoff auf der linken und Sauerstoff auf der rechten Seite geschrieben, so dass sich stattdessen \(HNO_3\) ergibt. Tatsächlich haben alle sechs gängigen starken Säuren, die wir in Kapitel 4 kennen gelernt haben, \(pK_a\)-Werte unter Null, was bedeutet, dass sie eher dazu neigen, ein Proton zu verlieren als das \(H_3O^+\)-Ion. Umgekehrt sind die konjugierten Basen dieser starken Säuren schwächere Basen als Wasser. Folglich liegen die Protonen-Transfer-Gleichgewichte für diese starken Säuren weit rechts, und die Zugabe einer der üblichen starken Säuren zu Wasser führt zu einer im Wesentlichen stöchiometrischen Reaktion der Säure mit Wasser unter Bildung einer Lösung des \(H_3O^+\)-Ions und der konjugierten Base der Säure.
Obwohl \(K_a\) für \(HI\) etwa 108 größer ist als \(K_a\) für \(HNO_3\), ergibt die Reaktion von \(HI\) oder \(HNO_3\) mit Wasser eine im Wesentlichen stöchiometrische Lösung von \(H_3O^+\) und I- oder \(NO_3^-\). In der Tat enthält eine 0,1 M wässrige Lösung einer beliebigen starken Säure 0,1 M \(H_3O^+\), unabhängig von der Identität der starken Säure. Dieses Phänomen wird als Nivellierungseffekt bezeichnet: Jede Spezies, die eine stärkere Säure als die konjugierte Säure des Wassers (\(H_3O^+\)) ist, wird in wässriger Lösung auf die Stärke von \(H_3O^+\) nivelliert, weil \(H_3O^+\) die stärkste Säure ist, die im Gleichgewicht mit Wasser existieren kann. Folglich ist es unmöglich, zwischen den Stärken von Säuren wie HI und HNO3 in wässriger Lösung zu unterscheiden, und es muss ein alternativer Ansatz verwendet werden, um ihre relativen Säurestärken zu bestimmen.
Eine Methode ist die Verwendung eines Lösungsmittels wie wasserfreie Essigsäure. Da Essigsäure eine stärkere Säure als Wasser ist, muss sie auch eine schwächere Base sein, mit einer geringeren Tendenz, ein Proton zu akzeptieren als \(H_2O\). Messungen der Leitfähigkeit von 0,1 M Lösungen von HI und \(HNO_3\) in Essigsäure zeigen, dass HI vollständig dissoziiert ist, \(HNO_3\) jedoch nur teilweise dissoziiert ist und sich in diesem Lösungsmittel wie eine schwache Säure verhält. Dieses Ergebnis sagt uns eindeutig, dass HI eine stärkere Säure ist als \(HNO_3\). Die relative Reihenfolge der Säurestärken und die ungefähren \(K_a\)- und \(pK_a\)-Werte für die starken Säuren am Anfang der Tabelle \(\PageIndex{1}\) wurden anhand solcher Messungen und verschiedener nichtwässriger Lösungsmittel ermittelt.
In wässrigen Lösungen ist \(H_3O^+\) die stärkste Säure und \(OH^-\) die stärkste Base, die mit \(H_2O\) im Gleichgewicht stehen kann.
Der Nivellierungseffekt gilt auch für Lösungen von starken Basen: In wässriger Lösung wird jede Base, die stärker als OH- ist, auf die Stärke von OH- nivelliert, weil OH- die stärkste Base ist, die im Gleichgewicht mit Wasser existieren kann. Salze wie \(K_2O\), \(NaOCH_3\) (Natriummethoxid) und \(NaNH_2\) (Natriumamid oder Natriumamid), deren Anionen die konjugierten Basen von Spezies sind, die in der Tabelle \(\PageIndex{2}\) unterhalb von Wasser liegen würden, sind allesamt starke Basen, die im Wesentlichen vollständig (und oft heftig) mit Wasser reagieren, wobei sie ein Proton aufnehmen und eine Lösung von \(OH^-\) und dem entsprechenden Kation ergeben:
\
\
\
Weitere Beispiele, denen man begegnen kann, sind Kaliumhydrid (\(KH\)) und metallorganische Verbindungen wie Methyllithium (\(CH_3Li\)).
Polyprotische Säuren und Basen
Wie Sie gelernt haben, enthalten polyprotische Säuren wie \(H_2SO_4\), \(H_3PO_4\) und \(H_2CO_3\) mehr als ein ionisierbares Proton, und die Protonen gehen schrittweise verloren. Die vollständig protonierte Spezies ist immer die stärkste Säure, da es einfacher ist, ein Proton aus einem neutralen Molekül zu entfernen als aus einem negativ geladenen Ion. Daher nimmt die Säurestärke mit dem Verlust nachfolgender Protonen ab, und dementsprechend steigt der \(pK_a\). Betrachten wir zum Beispiel \(H_2SO_4\):
\
Das Gleichgewicht in der ersten Reaktion liegt weit rechts, was bedeutet, dass \(H_2SO_4\) eine starke Säure ist. Im Gegensatz dazu sind bei der zweiten Reaktion sowohl \(HSO_4^-\) als auch \(SO_4^{2-}\) in nennenswerten Mengen im Gleichgewicht vorhanden.
Bei einer polyprotischen Säure nimmt die Säurestärke ab und der \(pK_a\) steigt mit dem aufeinanderfolgenden Verlust jedes Protons.
Das Hydrogensulfat-Ion (\(HSO_4^-\)) ist sowohl die konjugierte Base von \(H_2SO_4\) als auch die konjugierte Säure von \(SO_4^{2-}\). Genau wie Wasser kann HSO4- also entweder als Säure oder als Base wirken, je nachdem, ob der andere Reaktant eine stärkere Säure oder eine stärkere Base ist. Umgekehrt ist das Sulfat-Ion (\(SO_4^{2-}\)) eine polyprotische Base, die schrittweise zwei Protonen aufnehmen kann:
\
\
Wie bei jedem anderen konjugierten Säure-Base-Paar sind die Stärken der konjugierten Säuren und Basen durch \(pK_a\) + \(pK_b\) = pKw verknüpft. Betrachten wir zum Beispiel das konjugierte Säure-Basen-Paar HSO_4^-/ SO_4^{2-}\). Aus der Tabelle \(\PageIndex{1}\) geht hervor, dass der \(pK_a\) von \(HSO_4^-\) 1,99 beträgt. Folglich ist der \(pK_b\) von \(SO_4^{2-}\) 14,00 – 1,99 = 12,01. Sulfat ist also eine eher schwache Base, während \(OH^-\) eine starke Base ist, so dass das in Gleichung \(\ref{16.6}\) dargestellte Gleichgewicht nach links liegt. Das \(HSO_4^-\)-Ion ist ebenfalls eine sehr schwache Base (\(pK_a\) von \(H_2SO_4\) = 2,0, \(pK_b\) von \(HSO_4^- = 14 – (-2,0) = 16\), was dem entspricht, was wir für die konjugierte Base einer starken Säure erwarten.
Beispiel \(\PageIndex{2}\)
Vorhersagen Sie, ob das Gleichgewicht für jede Reaktion wie geschrieben links oder rechts liegt.
- \(NH^+_{4(aq)}+PO^{3-}_{4(aq)} \rightleftharpoons NH_{3(aq)}+HPO^{2−}_{4(aq)}\)
- \(CH_3CH_2CO_2H_{(aq)}+CN^−_{(aq)} \rightleftharpoons CH_3CH_2CO^-_{2(aq)}+HCN_{(aq)}\)
Gegeben: ausgeglichene chemische Gleichung
Gefragt: Gleichgewichtslage
Strategie:
Identifizieren Sie die konjugierten Säure-Base-Paare in jeder Reaktion. Bestimmen Sie dann anhand der Tabellen \(\PageIndex{1}\)und\(\PageIndex{2}\) sowie der Abbildung \(\PageIndex{2}\), welches die stärkere Säure bzw. Base ist. Das Gleichgewicht begünstigt immer die Bildung des schwächeren Säure-Base-Paares.
Lösung:
Die konjugierten Säure-Base-Paare sind \(NH_4^+/NH_3\) und \(HPO_4^{2-}/PO_4^{3-}\). Nach den Tabellen \(\PageIndex{1}\) und \(\PageIndex{2}\) ist \(NH_4^+\) eine stärkere Säure (\(pK_a = 9.25\)) als \(HPO_4^{2-}\) (pKa = 12,32), und \(PO_4^{3-}\) ist eine stärkere Base (\(pK_b = 1,68\)) als \(NH_3\) (\(pK_b = 4,75\)). Das Gleichgewicht wird daher rechts liegen und die Bildung des schwächeren Säure-Base-Paares begünstigen:
\
Die konjugierten Säure-Base-Paare sind \(CH_3CH_2CO_2H/CH_3CH_2CO_2^-\) und \(HCN/CN^-\). Nach der Tabelle \(\PageIndex{1}\) ist HCN eine schwache Säure (pKa = 9,21) und \(CN^-\) eine mäßig schwache Base (pKb = 4,79). Propionsäure (\(CH_3CH_2CO_2H\)) ist jedoch nicht in der Tabelle \(\PageIndex{1}\) aufgeführt. In einer solchen Situation ist es am besten, nach einer ähnlichen Verbindung zu suchen, deren Säure-Base-Eigenschaften aufgeführt sind. Beispielsweise sind Propionsäure und Essigsäure bis auf die an das Kohlenstoffatom der Carbonsäure gebundenen Gruppen identisch (\(\ce{-CH_2CH_3}\) versus \(\ce{-CH_3}\)), so dass man erwarten könnte, dass die beiden Verbindungen ähnliche Säure-Base-Eigenschaften aufweisen. Insbesondere würde man erwarten, dass der \(pK_a\) von Propionsäure ähnlich groß ist wie der \(pK_a\) von Essigsäure. (Tatsächlich liegt der \(pK_a\) von Propionsäure bei 4,87, verglichen mit 4,76 für Essigsäure, was Propionsäure zu einer etwas schwächeren Säure als Essigsäure macht.) Propionsäure sollte also eine wesentlich stärkere Säure sein als \(HCN\). Da die stärkere Säure die schwächere konjugierte Base bildet, sagen wir voraus, dass Cyanid eine stärkere Base sein wird als Propionat. Das Gleichgewicht wird also rechts liegen und die Bildung des schwächeren Säure-Base-Paares begünstigen:
\
Übung \(\PageIndex{1}\)
Vorhersagen Sie, ob das Gleichgewicht für jede Reaktion wie geschrieben links oder rechts liegt.
- \(H_2O_{(l)}+HS^-_{(aq)} \rightleftharpoons OH^−_{(aq)}+H_2S_{(aq)}\)
- \(HCO^−_{2(aq)}+HSO^−_{4(aq)} \rightleftharpoons HCO_2H_{(aq)}+SO^{2-}_{4(aq)}\)
Antwort a
links
Antwort b
links
Zusammenfassung
Säure-Base-Reaktionen enthalten immer zwei konjugierte Säure-Base-Paare. Jede Säure und jede Base hat eine zugehörige Ionisationskonstante, die ihrer Säure- oder Basenstärke entspricht. Zwei Spezies, die sich nur durch ein Proton unterscheiden, bilden ein konjugiertes Säure-Base-Paar. Die Größe der Gleichgewichtskonstante für eine Ionisierungsreaktion kann zur Bestimmung der relativen Stärke von Säuren und Basen verwendet werden. Für eine wässrige Lösung einer schwachen Säure wird die Dissoziationskonstante als Säureionisationskonstante (\(K_a\)) bezeichnet. In ähnlicher Weise ist die Gleichgewichtskonstante für die Reaktion einer schwachen Base mit Wasser die Basenionisationskonstante (\(K_b\)). Für jedes konjugierte Säure-Base-Paar ist \(K_aK_b = K_w\). Kleinere Werte von \(pK_a\) entsprechen größeren Säureionisationskonstanten und damit stärkeren Säuren. Umgekehrt entsprechen kleinere Werte von \(pK_b\) größeren Ionisationskonstanten von Basen und damit stärkeren Basen. Bei 25 °C ist \(pK_a + pK_b = 14,00\). Säure-Base-Reaktionen verlaufen immer in der Richtung, in der das schwächere Säure-Base-Paar entsteht. Keine Säure, die stärker ist als \(H_3O^+\), und keine Base, die stärker ist als \(OH^-\), kann in wässriger Lösung existieren, was zu dem als Nivellierungseffekt bekannten Phänomen führt. Polyprotische Säuren (und Basen) verlieren (und gewinnen) schrittweise Protonen, wobei die vollständig protonierte Spezies die stärkste Säure und die vollständig deprotonierte Spezies die stärkste Base ist.
Schlüsselgleichungen
- Säureionisationskonstante: \=\dfrac{}{} \]
- Base-Ionisationskonstante: \= \dfrac{}{} \]
- Beziehung zwischen \(K_a\) und \(K_b\) eines konjugierten Säure-Base-Paares: \
- Definition von \(pK_a\): \ \
- Definition von \(pK_b\): \ \
- Beziehung zwischen \(pK_a\) und \(pK_b\) eines konjugierten Säure-Base-Paares: \ \
Autoren und Verantwortliche
-
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook