Lernziele
- Die 3D-Darstellung von elektronischen Orbitalen verstehen
Ein Orbital ist die quantenmechanische Verfeinerung des Bohrschen Orbits. Im Gegensatz zu seinem Konzept einer einfachen Kreisbahn mit festem Radius sind Orbitale mathematisch abgeleitete Bereiche des Raums mit unterschiedlichen Wahrscheinlichkeiten, ein Elektron zu enthalten.
Eine Möglichkeit der Darstellung von Elektronenwahrscheinlichkeitsverteilungen wurde zuvor anhand des 1s-Orbitals von Wasserstoff illustriert. Da Ψ2 die Wahrscheinlichkeit angibt, ein Elektron in einem bestimmten Raumvolumen (z. B. einem Kubikpikometer) zu finden, ist eine Darstellung von Ψ2 in Abhängigkeit von der Entfernung vom Kern (r) eine Darstellung der Wahrscheinlichkeitsdichte. Das 1s-Orbital ist sphärisch symmetrisch, so dass die Wahrscheinlichkeit, ein 1s-Elektron an einem beliebigen Punkt zu finden, nur von seinem Abstand zum Kern abhängt. Die Wahrscheinlichkeitsdichte ist am größten bei \(\(r\) = 0\) (am Kern) und nimmt mit zunehmender Entfernung stetig ab. Bei sehr großen Werten von r ist die Elektronenwahrscheinlichkeitsdichte sehr klein, aber nicht Null.
Im Gegensatz dazu können wir die radiale Wahrscheinlichkeit (die Wahrscheinlichkeit, ein 1s-Elektron in einem Abstand \(r\) vom Kern zu finden) berechnen, indem wir die Wahrscheinlichkeiten, dass sich ein Elektron an allen Punkten einer Reihe von x Kugelschalen mit dem Radius r1, r2, r3,…, rx – 1, rx befindet, zusammenzählen. In der Tat unterteilen wir das Atom in sehr dünne konzentrische Schalen, ähnlich wie die Schichten einer Zwiebel (Abbildung \(\PageIndex{1a}\)), und berechnen die Wahrscheinlichkeit, ein Elektron auf jeder Kugelschale zu finden. Erinnern Sie sich daran, dass die Elektronenwahrscheinlichkeitsdichte bei \(r\) = 0 am größten ist (Abbildung \(\PageIndex{1b}\)), so dass die Dichte der Punkte bei den kleinsten Kugelschalen in Teil (a) in Abbildung \(\PageIndex{1}\) am größten ist. Dagegen ist die Oberfläche jeder Kugelschale gleich \(4πr^2\), die mit zunehmendem \(r\) sehr schnell zunimmt (Abbildung \(\PageIndex{1c}\)). Da die Oberfläche der Kugelschalen mit zunehmendem \(r\) schneller zunimmt als die Elektronenwahrscheinlichkeitsdichte abnimmt, hat die Darstellung der radialen Wahrscheinlichkeit ein Maximum bei einem bestimmten \(r\) Abstand (Abbildung \(\PageIndex{1d}\)). Wenn \(r\) sehr klein ist, ist die Oberfläche einer Kugelschale so klein, dass die Gesamtwahrscheinlichkeit, ein Elektron in der Nähe des Kerns zu finden, sehr gering ist; am Kern verschwindet die Elektronenwahrscheinlichkeit (Abbildung \(\PageIndex{1d}\)).

Für das Wasserstoffatom tritt die Spitze in der Darstellung der radialen Wahrscheinlichkeit bei \(r\) = 0,529 Å (52,9 pm) auf, was genau dem von Boh\(r\) berechneten Radius für die n = 1 Bahn entspricht. Somit ist der wahrscheinlichste Radius, der sich aus der Quantenmechanik ergibt, identisch mit dem Radius, der von der klassischen Mechanik berechnet wurde. Im Bohr’schen Modell wurde jedoch davon ausgegangen, dass sich das Elektron zu 100 % der Zeit in diesem Abstand befindet, während es sich im Schrödinge-Modell nur zu einem Teil der Zeit in diesem Abstand befindet. Der Unterschied zwischen den beiden Modellen ist auf das wellenförmige Verhalten des Elektrons und die Heisenbergsche Unschärferelation zurückzuführen.
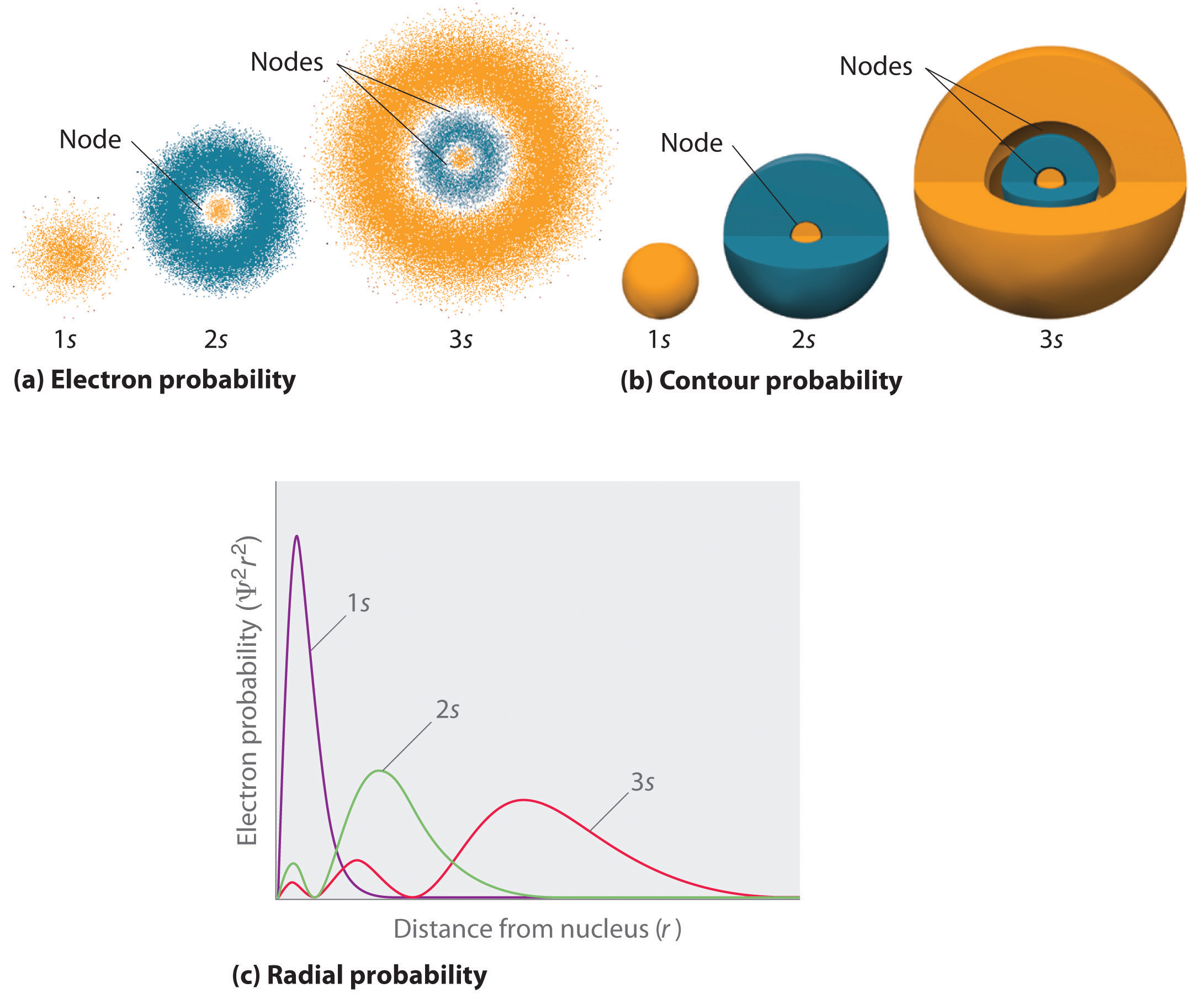
Abbildung \(\PageIndex{2}\) vergleicht die Elektronenwahrscheinlichkeitsdichten für die Wasserstoff-1s, -2s und -3s-Orbitale. Man beachte, dass alle drei sphärisch symmetrisch sind. Bei den 2s und 3s Orbitalen (und auch bei allen anderen s-Orbitalen) fällt die Elektronenwahrscheinlichkeitsdichte mit zunehmendem \(r\) nicht gleichmäßig ab. Stattdessen ist in den radialen Wahrscheinlichkeitsdiagrammen (Abbildung \(\PageIndex{2c}\)) eine Reihe von Minima und Maxima zu beobachten. Die Minima entsprechen kugelförmigen Knoten (Regionen mit Elektronenwahrscheinlichkeit Null), die sich mit kugelförmigen Regionen mit Elektronenwahrscheinlichkeit ungleich Null abwechseln. Die Existenz dieser Knoten ist eine Folge von Änderungen der Wellenphase in der Wellenfunktion Ψ.
s-Orbitale (l=0)
Drei Dinge passieren mit s-Orbitalen, wenn n zunimmt (Abbildung \(\PageIndex{2}\)):
- Sie werden größer und erstrecken sich weiter vom Kern weg.
- Sie enthalten mehr Knotenpunkte. Dies ist vergleichbar mit einer stehenden Welle, die Bereiche mit großer Amplitude aufweist, die durch Knoten, d. h. Punkte mit einer Amplitude von Null, getrennt sind.
- Bei einem bestimmten Atom wird die Energie der s-Orbitale mit zunehmendem n ebenfalls höher, weil der Abstand zum Kern größer wird.
Orbitale werden im Allgemeinen als dreidimensionale Flächen gezeichnet, die 90 % der Elektronendichte einschließen, wie dies für die 1s, 2s und 3s Orbitale des Wasserstoffs in Teil (b) in Abbildung \(\PageIndex{2}\) gezeigt wurde. Obwohl solche Zeichnungen die relativen Größen der Orbitale zeigen, zeigen sie normalerweise nicht die kugelförmigen Knoten in den 2s und 3s Orbitalen, weil die kugelförmigen Knoten innerhalb der 90% Oberfläche liegen. Glücklicherweise sind die Positionen der sphärischen Knoten für die chemische Bindung nicht wichtig.
p-Orbitale (l=1)
Nur s-Orbitale sind sphärisch symmetrisch. Mit steigendem Wert von l nimmt die Anzahl der Orbitale in einer bestimmten Unterschale zu, und die Formen der Orbitale werden komplexer. Da die 2p-Unterschale l = 1 hat, gibt es bei drei Werten von ml (-1, 0 und +1) drei 2p-Orbitale.
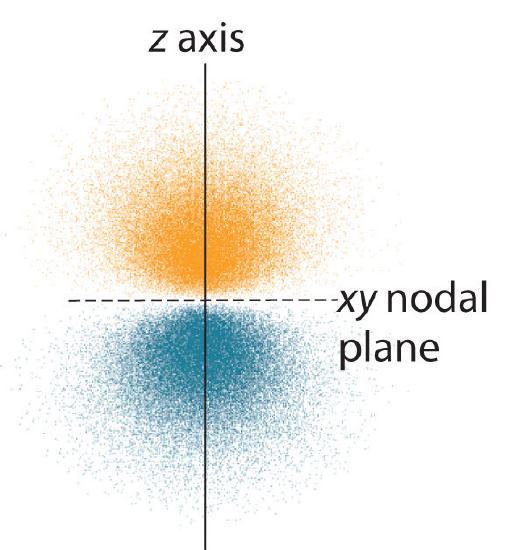
Die Elektronenwahrscheinlichkeitsverteilung für eines der Wasserstoff-2p-Orbitale ist in Abbildung \(\PageIndex{3}\) dargestellt. Da dieses Orbital zwei entlang der z-Achse angeordnete Lappen mit einer Elektronendichte von Null in der xy-Ebene aufweist (d. h. die xy-Ebene ist eine Knotenebene), handelt es sich um ein \(2p_z\) Orbital. Wie in Abbildung \(\PageIndex{4}\) dargestellt, haben die beiden anderen 2p-Orbitale die gleiche Form, liegen aber entlang der x-Achse (\(2p_x\)) bzw. der y-Achse (\(2p_y\)). Man beachte, dass jedes p-Orbital nur eine Knotenebene hat. In jedem Fall ist die Phase der Wellenfunktion fo\(r\) jedes der 2p-Orbitale positiv fo\(r\) die Keule, die auf die positive Achse zeigt und negativ fo\(r\) die Keule, die auf die negative Achse zeigt. Es ist wichtig zu betonen, dass diese Vorzeichen der Phase der Welle entsprechen, die die Elektronenbewegung beschreibt, und nicht den positiven o\(r\) negativen Ladungen.
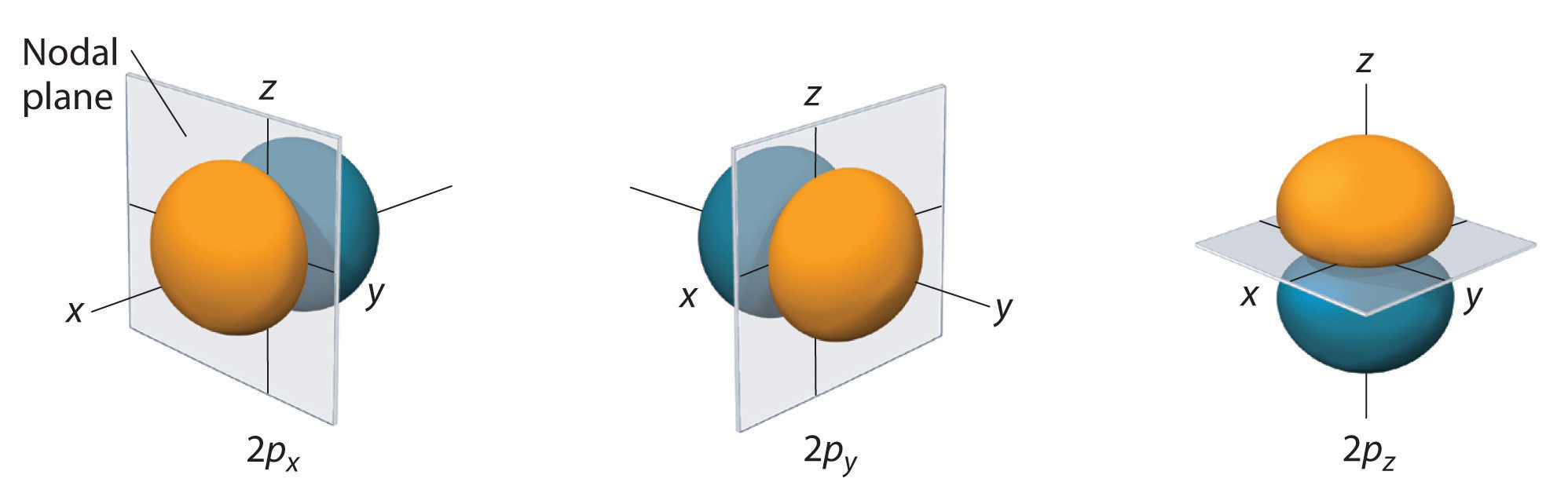
Die dargestellten Flächen umschließen 90 % der gesamten Elektronenwahrscheinlichkeit fo\(r\) der 2px-, 2py- und 2pz-Orbitale. Jedes Orbital ist entlang der durch den tiefgestellten Index angegebenen Achse ausgerichtet, und eine Knotenebene, die senkrecht zu dieser Achse steht, halbiert jedes 2p-Orbital. Die Phase der Wellenfunktion ist positiv (orange) in dem Bereich des Raums, in dem x, y, o\(r\) z positiv ist, und negativ (blau), wo x, y, o\(r\) z negativ ist. Genau wie bei den s-Orbitalen nehmen die Größe und Komplexität der p-Orbitale fo\(r\) jedes Atoms mit der Zunahme der Hauptquantenzahl n zu. Die Formen der 90%-Wahrscheinlichkeitsflächen der 3p-, 4p- und höherenergetischen p-Orbitale sind jedoch im Wesentlichen die gleichen wie in Abbildung \(\PageIndex{4}\).
d-Orbitale (l=2)
Unterschalen mit l = 2 haben fünf d-Orbitale; die erste Hauptschale, die eine d-Unterschale hat, entspricht n = 3. Die fünf d-Orbitale haben ml-Werte von -2, -1, 0, +1 und +2.
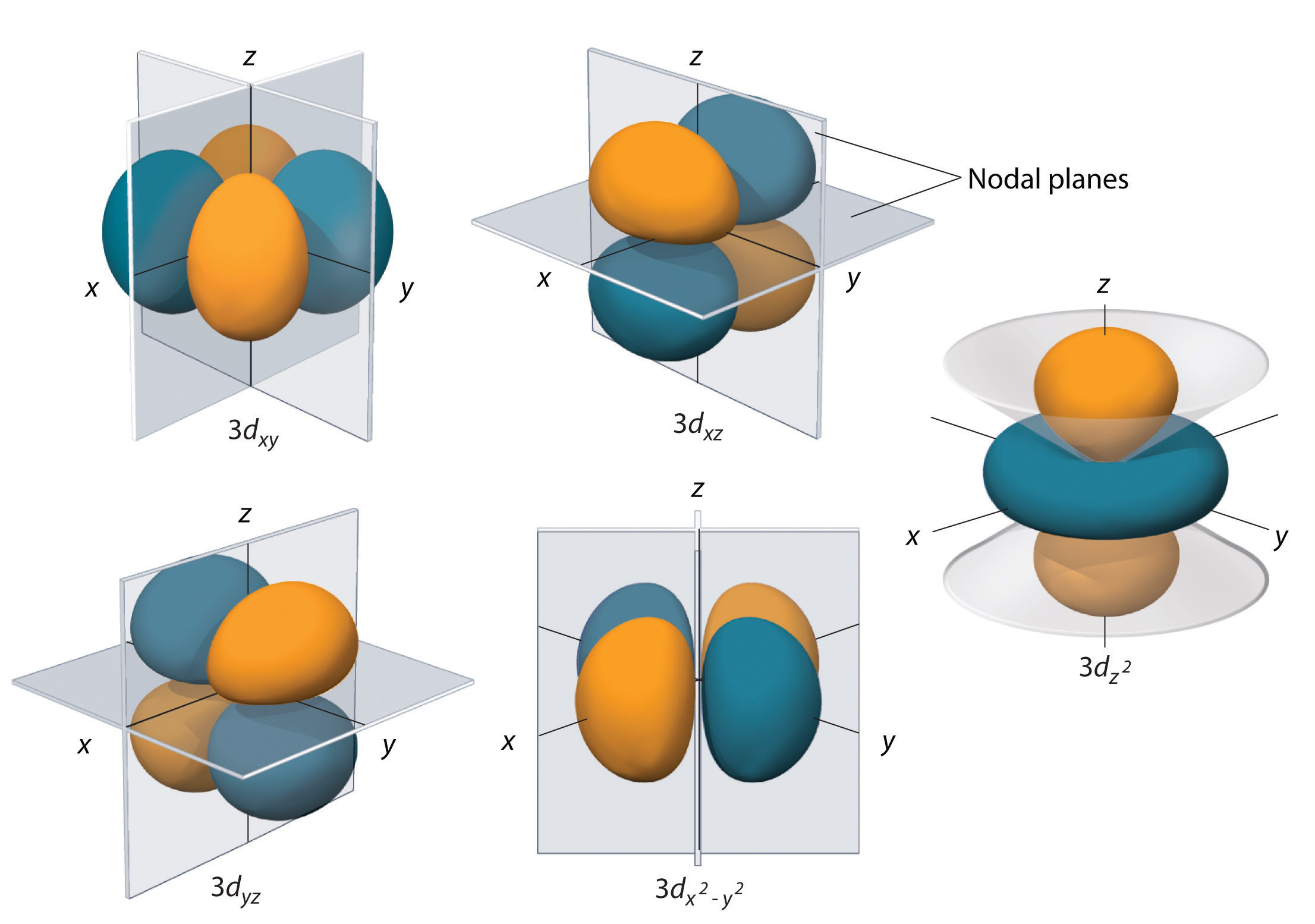
Die 3d-Orbitale des Wasserstoffs, die in Abbildung \(\PageIndex{5}\) dargestellt sind, haben eine komplexere Form als die 2p-Orbitale. Alle fünf 3d-Orbitale enthalten zwei Knotenflächen, verglichen mit einer fo\(r\) pro p-Orbital und null fo\(r\) pro s-Orbital. In drei der d-Orbitale sind die Lappen der Elektronendichte zwischen den Ebenen x und y, x und z sowie y und z ausgerichtet; diese Orbitale werden als \(3d_{xy}\), \)3d_{xz}\) bzw. \(3d_{yz}\) bezeichnet. Ein viertes d-Orbital hat Lappen, die entlang der x- und y-Achse liegen; dies ist das \(3d_{x^2-y^2}\) Orbital. Das fünfte 3d-Orbital, das so genannte \(3d_{z^2}\)-Orbital, hat eine einzigartige Form: Es sieht aus wie ein \(2p_z\)-Orbital in Kombination mit einem zusätzlichen Donut der Elektronenwahrscheinlichkeit in der xy-Ebene. Trotz seiner eigentümlichen Form ist das \(3d_{z^2}\)-Orbital mathematisch äquivalent zu den anderen \(r\)-Orbitalen und hat die gleiche Energie. Im Gegensatz zu den p-Orbitalen ist die Phase der Wellenfunktion bei den d-Orbitalen für die gegenüberliegenden Lappenpaare dieselbe. Wie in Abbildung \(\PageIndex{5}\) dargestellt, ist die Phase der Wellenfunktion positiv für die beiden Keulen des \(dz^2\)-Orbitals, die entlang der z-Achse liegen, während die Phase der Wellenfunktion negativ für den Donut der Elektronendichte in der xy-Ebene ist. Wie bei den s- und p-Orbitalen nimmt mit zunehmendem n auch die Größe der d-Orbitale zu, aber die Gesamtformen bleiben ähnlich wie in Abbildung \(\PageIndex{5}\).
f-Orbitale (l=3)
Hauptschalen mit n = 4 können Unterschalen mit l = 3 und ml-Werten von -3, -2, -1, 0, +1, +2 und +3 haben. Diese Unterschalen bestehen aus sieben f-Orbitalen. Jedes f-Orbital hat drei Knotenflächen, so dass diei\(r\)-Formen komplex sind. Da f-Orbitale für die Zwecke von ou\(r\) nicht besonders wichtig sind, werden sie nicht weiter erörtert, und Orbitale mit hohen l-Werten werden überhaupt nicht besprochen.
Orbitalenergien
Obwohl wir die Formen von Orbitalen besprochen haben, haben wir wenig über diei\(r\) vergleichbaren Energien gesagt. Wir beginnen unsere Erörterung der Orbitalenergien mit der Betrachtung von Atomen oder Ionen mit nur einem einzigen Elektron (wie H oder He+).
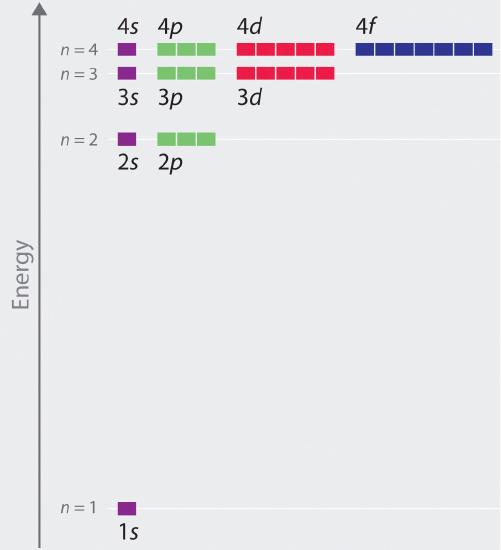
Die relativen Energien der Atomorbitale mit n ≤ 4 für ein Wasserstoffatom sind in Abbildung \(\PageIndex{6}\) dargestellt; beachten Sie, dass die Orbitalenergien nur von der Hauptquantenzahl n abhängen. Folglich sind die Energien der 2s und 2p Orbitalen des Wasserstoffs gleich; die Energien der 3s, 3p und 3d Orbitalen sind gleich; und so weiter. Die Quantenmechanik sagt voraus, dass im Wasserstoffatom alle Orbitale mit dem gleichen Wert von n (z. B. die drei 2p-Orbitale) entartet sind, d. h. sie haben die gleiche Energie. Die Orbitalenergien, die für Wasserstoff mit Hilfe der Quantenmechanik ermittelt wurden, entsprechen genau den von Bohr berechneten zulässigen Energien (r\(r\)). Im Gegensatz zum Bohr’schen Modell, das für jedes Energieniveau nur ein Orbital zuließ, sagt die Quantenmechanik jedoch voraus, dass es in der n = 2-Hauptschale 4 Orbitale mit unterschiedlichen Elektronendichteverteilungen gibt (ein 2s-Orbital und drei 2p-Orbitale), 9 in der n = 3-Hauptschale und 16 in der n = 4-Hauptschale.Die unterschiedlichen Werte von l und ml für die einzelnen Orbitale innerhalb einer bestimmten Hauptschale sind für das Verständnis der Emissions- und Absorptionsspektren des Wasserstoffatoms unter den meisten Bedingungen nicht wichtig, erklären aber die Aufspaltung der Hauptlinien, die beobachtet wird, wenn Wasserstoffatome in ein Magnetfeld gebracht werden. Abbildung \(\PageIndex{6}\) zeigt, dass sich die Energieniveaus mit zunehmendem Wert von n, wie aufgrund der 1/n2-Abhängigkeit der Orbitalenergien erwartet, einander annähern.
Die Energien der Orbitale in jeder Spezies mit nur einem Elektron lassen sich durch eine Mini-Variante der Bohrschen Gleichung berechnen, die auf andere Ein-Elektronen-Spezies ausgedehnt werden kann, indem die Kernladung \(Z\) (die Anzahl der Protonen im Kern) einbezogen wird:
\
Im Allgemeinen nehmen sowohl die Energie als auch der Radius ab, wenn die Kernladung (r\) zunimmt. Die stabilsten Orbitale (die mit der niedrigsten Energie) sind also diejenigen, die dem Kern am nächsten sind. Fo\(r\) Beispiel: Im Grundzustand des Wasserstoffatoms befindet sich das einzelne Elektron im 1s-Orbital, während das Atom im ersten angeregten Zustand Energie absorbiert hat und das Elektron in eines der n = 2-Orbitale befördert wurde. Bei Ionen mit nur einem einzigen Elektron hängt die Energie eines bestimmten Orbitales nur von n ab, und alle Unterschalen innerhalb einer Hauptschale, wie die Orbitale \(p_x\), \(p_y\) und \(p_z\), sind entartet.
Zusammenfassung
Die fou\(r\) chemisch wichtigen Arten von Atomorbitalen entsprechen den Werten \(\ell = 0\), \(1\), \(2\) und \(3\). Orbitale mit \(\ell = 0\) sind s-Orbitale und sphärisch symmetrisch, wobei die größte Wahrscheinlichkeit besteht, dass das Elektron am Kern zu finden ist. Alle Orbitale mit Werten von \(n > 1\) und \(ell = 0\) enthalten einen o\(r\) mehr Knoten. Orbitale mit \(\ell = 1\) sind p-Orbitale und enthalten eine Knotenebene, die den Kern einschließt, was zu einer Hantelform führt. Orbitale mit \(\ell = 2\) sind d-Orbitale und haben komplexere Formen mit mindestens zwei Nodalflächen. Orbitale mit \(\ell = 3\) sind f-Orbitale, die noch komplexer sind.
Da der durchschnittliche Abstand zum Kern die Energie eines Elektrons bestimmt, ist jedem Atomorbital mit einer bestimmten Quantenzahl eine bestimmte Energie zugeordnet, die Orbitalenergie.
\
In Atomen o\(r\) Ionen mit nur einem einzigen Elektron haben alle Orbitale mit dem gleichen Wert von \(n\) die gleiche Energie (sie sind entartet), und die Energien der Hauptschalen nehmen mit zunehmendem \(n\) gleichmäßig zu. Ein o\(r\)-Ion, dessen Elektron(en) sich im niedrigsten Orbital befinden, wird als Grundzustand bezeichnet, während ein o\(r\)-Ion, bei dem ein o\(r\)-Elektron mehr Orbitale mit höherer Energie besetzt, als angeregter Zustand bezeichnet wird.
Beiträger und Zuordnungen
-
Änderung durch Joshua Halpern (Howard University)