Eine Asymptote ist eine Linie, der sich ein Graph nähert, die er aber nicht schneidet.
In dieser Lektion lernen wir, wie man vertikale Asymptoten, horizontale Asymptoten und schräge Asymptoten von rationalen Funktionen findet.
Verwandte Themen:
Weitere Lektionen zu Calculus

Das folgende Diagramm zeigt die verschiedenen Arten von Asymptoten: horizontale Asymptoten, vertikale Asymptoten und schräge Asymptoten. Scrollen Sie auf der Seite nach unten, um weitere Beispiele und Lösungen zum Auffinden von Asymptoten zu finden.

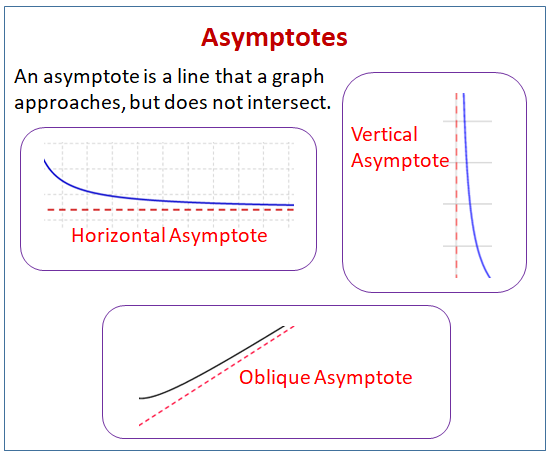
Wie bestimmt man die vertikale Asymptote?

Methode 1: Verwenden Sie die Definition der vertikalen Asymptote

Die Linie x = a wird als vertikale Asymptote der Kurve y = f(x) bezeichnet, wenn mindestens eine der folgenden Aussagen wahr ist.

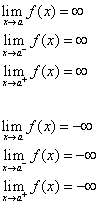
Methode 2:

Für rationale Funktionen sind vertikale Asymptoten senkrechte Linien, die den Nullstellen des Nenners entsprechen.
Gibt man die rationale Funktion f(x)

Schritt 1: Schreibe f(x) in reduzierter Form

Schritt 2: Wenn x – c ein Faktor im Nenner ist, dann ist x = c die vertikale Asymptote.

Beispiel:

Finde die vertikalen Asymptoten von

Lösung:

Methode 1: Verwende die Definition der vertikalen Asymptote.

Wenn x nahe bei 3, aber größer als 3 ist, dann ist der Nenner x – 3 eine kleine positive Zahl und 2x ist nahe bei 8. Also ist eine große positive Zahl.

Intuitiv sehen wir, dass

Gleichermaßen, wenn x nahe bei 3, aber kleiner als 3 ist, dann ist x – 3 eine kleine negative Zahl und 2x ist nahe bei 8. Also ist eine große negative Zahl.

Die Linie x = 3 ist die vertikale Asymptote.

Methode 2:

Schritt 1: f(x) ist bereits in reduzierter Form.

Schritt 2: Der Nenner ist x – 3, also liegt die vertikale Asymptote bei x = 3.

Vertikale Asymptoten rationaler Funktionen finden

Worauf man achten muss, um vertikale Asymptoten rationaler Funktionen zu finden.

• Schrittweise Lösungen anzeigen

Vertikale Asymptoten rationaler Funktionen: Schnelles Auffinden

Beispiel für das Auffinden vertikaler Asymptoten rationaler Funktionen.

• Schrittweise Lösungen anzeigen

Wie findet man vertikale Asymptoten für rationale Funktionen

• Schrittweise Lösungen anzeigen

Wie bestimmt man die horizontale Asymptote?

Methode 1: Verwende die Definition der horizontalen Asymptote

Die Linie y = L wird als horizontale Asymptote der Kurve y = f(x) bezeichnet, wenn entweder

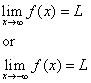
Methode 2:

Für die rationale Funktion f(x)

Wenn der Grad von x im Zähler kleiner ist als der Grad von x im Nenner, dann ist y = 0 die horizontale Asymptote.

Wenn der Grad von x im Zähler gleich dem Grad von x im Nenner ist, dann ist y = c, wobei sich c durch Division der führenden Koeffizienten ergibt.

Beispiel:

Bestimme die horizontale und vertikale Asymptote der Funktion.

Lösung:

Methode 1:

Trennen Sie Zähler und Nenner durch x.

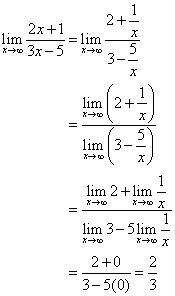
Die Linie ist die horizontale Asymptote.

Methode 2:

Der Grad von x im Zähler ist gleich dem Grad von x im Nenner.

Teilt man die führenden Koeffizienten, erhält man

Die Linie ist die horizontale Asymptote.

Verknüpfung zum Finden horizontaler Asymptoten rationaler Funktionen

Ein paar Tricks, die das Finden horizontaler Asymptoten rationaler Funktionen sehr einfach machen

• Schrittweise Lösungen anzeigen

Dieses Video gibt einen grundlegenden Überblick über horizontale Asymptoten. Wir bestimmen, ob die gegebenen rationalen Funktionen horizontale Asymptoten haben und welche das sind.

• Schrittweise Lösungen anzeigen

In diesem Video werden die Regeln für horizontale Asymptoten näher erläutert.

• Schrittweise Lösungen anzeigen

Schräge Asymptote oder schräge Asymptote

Einige Kurven haben Asymptoten, die schräg sind, das heißt, weder horizontal noch vertikal.

Wenn dann heißt die Linie y = mx + b schräge Asymptote, weil die vertikalen Abstände zwischen der Kurve y = f(x) und der Linie y = mx + b gegen 0 gehen.

Bei rationalen Funktionen treten schräge Asymptoten auf, wenn der Grad des Zählers um eins größer ist als der Grad des Nenners. In einem solchen Fall kann die Gleichung der schiefen Asymptote durch lange Division gefunden werden.

Beispiel:

Finde die Asymptoten der Funktion

Lösung:

Da der Nenner x2 + 1 nie 0 ist, gibt es keine senkrechte Asymptote.

Da der Grad von x im Zähler größer ist als der Grad von x im Nenner, gibt es keine waagerechte Asymptote.

Da der Grad von x im Zähler um eins größer ist als der Grad von x im Nenner, können wir die lange Division verwenden, um die schräge Asymptote zu erhalten.

Die Linie y = x ist also die schräge Asymptote.

Schräge Asymptoten von rationalen Funktionen finden

In diesem Video wird beschrieben, wann eine rationale Funktion eine schräge Asymptote hat, es wird kurz beschrieben, was eine schräge Asymptote ist, und dann werden zwei Beispiele gezeigt.

• Schrittweise Lösungen anzeigen

Asymptoten einer rationalen Funktion finden (vertikal, horizontal und schräg/schräg)

Dieses Video zeigt, wie man die vertikalen Asymptoten und eine schräge Asymptote einer rationalen Funktion findet.

• Schrittweise Lösungen anzeigen

Alle Asymptoten einer rationalen Funktion finden (vertikal, horizontal, schräg/schräg)

Hier betrachten wir eine Funktion und finden die vertikale Asymptote und stellen außerdem fest, dass es keine horizontalen Asymptoten gibt, aber eine schräge Asymptote existiert. Wir verwenden dann die lange Division, um die schräge Asymptote zu finden.

• Schrittweise Lösungen anzeigen

Testen Sie den kostenlosen Mathway-Rechner und Problemlöser unten, um verschiedene mathematische Themen zu üben. Probieren Sie die vorgegebenen Beispiele aus oder geben Sie Ihre eigene Aufgabe ein und überprüfen Sie Ihre Antwort anhand der schrittweisen Erklärungen.