Nachfolgend meine Meinung zu einigen Matheproblemen der angeblich „Common Core Mathe“ oder „neuen Mathe“, die im Internet kursieren. Meiner Meinung nach zeigen sie uns eine fehlgeleitete Umsetzung des CCS.

Denken Sie daran, dass nicht alles, was Sie in Mathebüchern oder im Internet sehen, auf der Grundlage des CCS richtig gemacht wird. In einigen der Beispiele, die man sieht, sieht es so aus, als ob die Leute den gesunden Menschenverstand über Bord werfen, wenn sie Matheaufgaben machen, um die Common Core Standards zu erfüllen!

Ich bin nicht überrascht, dass die Umsetzung an einigen Stellen „verpfuscht“ wurde. Die CCS sind für die meisten Lehrer eine solche Umstellung, dass sie viel Unterstützung und Nachschulung brauchen, bevor sie nach ihnen unterrichten können.

Ich war schon immer der Meinung, dass das Hauptproblem des Mathematikunterrichts in den öffentlichen Schulen darin besteht, dass viele Grundschullehrer die Mathematik nicht ausreichend verstehen, um sie schon in der Grundschule richtig zu unterrichten. Viele von ihnen verstehen zum Beispiel die Konzepte, das Warum und Wozu der Algorithmen, die sie unterrichten, nicht. Das ist nicht ihre Schuld – das Problem geht auf das zurück, was ihnen in der Lehrerausbildung und in ihrer eigenen Schulzeit beigebracht wurde.

Auch das Standarddokument selbst ist stellenweise schwer zu verstehen. Die Lektüre erfordert einige Überlegungen. Ich wünschte, jemand würde eine Broschüre herausgeben, die die Standards in einfacher Sprache und mit zahlreichen Beispielen erklärt.

Schlechte Beispiele für „Common Core“ oder „neue Mathematik“

Beispiel 1

Kürzlich sah ich auf Facebook ein Bild von Subtraktionsstrategien, das behauptete, es stamme aus einem Mathebuch für die erste Klasse und sei „Common Core Mathe.“

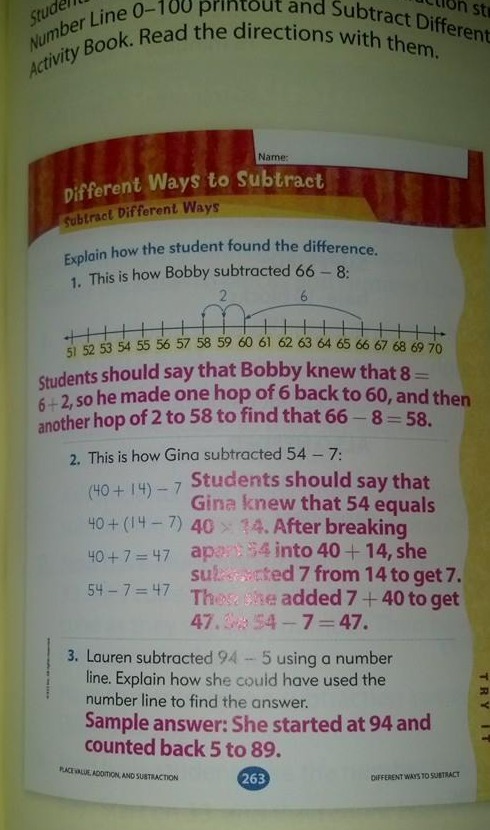
Ich denke, dass Methode 2 viel zu schwierig für die erste Klasse ist, und ich würde sogar Methode 1 für die zweite Klasse lassen.

Das Buch scheint jedoch nicht einmal mit den Common Core Standards übereinzustimmen. Die Standards für die 1. Klasse beinhalten diese Art von Subtraktionsproblemen einfach nicht!

Das ist, was wir in den Standards finden:

Addieren und Subtrahieren innerhalb von 20.
1.OA.5
Beziehen Sie das Zählen auf Addition und Subtraktion (z.B. indem Sie auf 2 zählen, um 2 zu addieren).
1.OA.6.
Addieren und subtrahieren Sie innerhalb von 20 und zeigen Sie, dass Sie Addition und Subtraktion innerhalb von 10 beherrschen. Strategien anwenden, wie z. B. weiterzählen; Zehnerzahlen bilden (z. B. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); eine Zahl in eine Zehnerzahl zerlegen (z. B. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); die Beziehung zwischen Addition und Subtraktion nutzen (z. B. wenn man weiß, dass 8 + 4 = 12 ist, weiß man auch, dass 12 – 8 = 4 ist); und gleichwertige, aber einfachere oder bekannte Summen bilden (z. B., Addieren von 6 + 7 durch Bilden des bekannten Äquivalents 6 + 6 + 1 = 12 + 1 = 13).

Das Lehrbuchbeispiel scheint 1.OA.6 oben ansprechen zu wollen, aber das bezieht sich eindeutig auf das Addieren und Subtrahieren innerhalb von 20, nicht auf größere Zahlen.

Später in den Standards für die 1. Klasse sehen wir zwei Standards, die mit dem Subtrahieren zweistelliger Zahlen (innerhalb von 100) zu tun haben:

1.NBT.5.
Geben Sie eine zweistellige Zahl, finden Sie geistig 10 mehr oder 10 weniger als die Zahl, ohne zu zählen; erklären Sie die Argumentation verwendet.
1.NBT.6.
Vielfache von 10 im Bereich 10-90 von Vielfachen von 10 im Bereich 10-90 (positive oder Null-Differenzen) subtrahieren, wobei konkrete Modelle oder Zeichnungen und Strategien verwendet werden, die auf dem Stellenwert, den Eigenschaften der Operationen und/oder der Beziehung zwischen Addition und Subtraktion beruhen; die Strategie mit einer schriftlichen Methode in Beziehung setzen und die verwendete Begründung erklären.
Maria’s note: Dies bedeutet Subtraktionen wie 34 – 20 oder 89 – 60.

aber keines davon umfasst Subtraktionen wie 54 – 7 oder 82 – 6. Diese sind in der 2. Klasse:

2.NBT.5
Fließend addieren und subtrahieren innerhalb von 100 unter Verwendung von Strategien, die auf dem Stellenwert, den Eigenschaften der Operationen und/oder der Beziehung zwischen Addition und Subtraktion basieren.

Beachten Sie, dass der Standard für die 2. Klasse nicht angibt, WIE man subtrahiert (ob man mentale Rechenstrategien verwendet oder Zahlen untereinander schreibt und borgt/zusammenfasst).

Beispiel 2

Von Houghton Mifflin, angeblich:

Juanita möchte ihren Freunden Tüten mit Aufklebern schenken. Sie möchte jedem Freund die gleiche Anzahl von Aufklebern schenken. Sie ist sich nicht sicher, ob sie 4 Tüten oder 6 Tüten Sticker braucht. Wie viele Sticker kann sie kaufen, damit keine Sticker übrig bleiben?

Das Stickerproblem hat mit dem Konzept des kleinsten gemeinsamen Vielfachen (LCM) zu tun. (Die Antwort ist, dass sie 12, 24, 36 oder ein beliebiges anderes Vielfaches von 12 Aufklebern kaufen sollte, denn dann kann sie sie entweder in 4 Tüten oder in 6 Tüten aufteilen.)

Sicher, die Aufgabe ist SEHR unklar und schlecht formuliert. Ich vermute, dass das Heft, in dem das steht, einfach unbearbeitet ist. Es ist nicht die Schuld der Normen selbst. Ich stimme Bart Goddard im Math Forum zu. Dies ist ein Symptom für den blinden Drang, „lebensnahe“ Aufgabenstellungen zu produzieren, die am Ende unsinnig sind.

Aus dem PDF-Dokument, in dem es erscheint, schließe ich, dass das Problem für die vierte Klasse ist, weil alle anderen Wortprobleme in dem Heft den Standards für die vierte Klasse entsprechen (Faktoren, Primzahlen). Aber die CCS enthalten nicht einmal das kleinste gemeinsame Vielfache in den Standards der 4. Klasse (es steht in der 6. Klasse)! Irgendetwas ist bei diesem Wortproblem wirklich schief gelaufen.

Beispiel 3

Auch das ist angeblich von Houghton Mifflin für die 1. Das entspricht der Norm, die ich oben schon zitiert habe:

Addieren und Subtrahieren innerhalb von 20.
1.OA.6.
Addieren und Subtrahieren innerhalb von 20, wobei die Fähigkeit zur Addition und Subtraktion innerhalb von 10 gezeigt wird. Strategien anwenden, wie z. B. weiterzählen; Zehnerzahlen bilden (z. B. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); eine Zahl bis zur Zehn zerlegen (z. B. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); die Beziehung zwischen Addition und Subtraktion nutzen (z. B., Wenn man weiß, dass 8 + 4 = 12 ist, weiß man auch, dass 12 – 8 = 4 ist); und das Bilden von gleichwertigen, aber einfacheren oder bekannten Summen (z.B. die Addition von 6 + 7 durch das Bilden des bekannten Äquivalents 6 + 6 + 1 = 12 + 1 = 13).

Zunächst einmal hat die Strategie des „Zehnerstellens“ mit ADDITION zu tun, nicht mit Subtraktion. Bei der Subtraktion nennt man das „Zerlegen einer Zahl, die zu einer Zehn führt“. In der Anleitung sollte es also heißen: „Welcher Weg führt zur Zerlegung einer Zahl, die zu einer Zehn führt?“ Ich halte es für völligen NONSENSE, von Schülern der ersten Klasse die Kenntnis einer solchen Terminologie zu verlangen.

Aber es gibt noch ein weiteres Problem. Wenn Sie alle Standards lesen, werden Sie feststellen, dass die Schüler an mehreren anderen Stellen aufgefordert werden, die verwendeten Überlegungen zu erläutern oder eine bestimmte visuelle Methode mit der Strategie in Verbindung zu bringen, aber NICHT in diesem Standard!

Ich sehe diesen Standard so, dass die Lehrer die verschiedenen erwähnten Strategien UNTERRICHTEN und den Schülern dann EINFACHE Additions- und Subtraktionsaufgaben innerhalb von 20 geben sollen, z. B. 15 – 8 und 10 – 6. Ich sehe NICHT, dass dieser Standard von den Schülern verlangt, dass sie erkennen, ob ein bestimmtes visuelles Modell zu einer bestimmten Strategie passt.

Auch hier sieht es so aus, als ob der Autor den gesunden Menschenverstand über Bord wirft… und die Standards nicht wirklich versteht.

Beispiel 4

Das folgende Beispiel ist sehr schlecht formuliert, aber das KONZEPT dahinter ist sehr gut und findet sich auch in Math Mammoth. Ich kann mir also denken, was sie wollen.

Du siehst fünf Quadrate. Färbe einige blau und den Rest rot. Das ist klar.

Dann färbe die Quadrate in der „Zahlenverbindung“ auf die gleiche Weise. Das Zahlenband geht zu diesen drei Kreisen. Ein Kind, das an einer Unterrichtsstunde teilgenommen hat, in der der Lehrer Zahlenbindungen unterrichtet hat, weiß hoffentlich, was das bedeutet. Es ist das gleiche Konzept wie eine Zahlenfamilie… die obere Zahl ist die Summe (5), und die Zahlen, die zu den unteren Kreisen gehören, entsprechen den Zahlen, die man blau und rot gefärbt hat, in diesem Fall 1 und 4.

Dann denke ich, dass die versteckten Partner auch die 1 und 4 sind. Zeigen Sie einem Erwachsenen 1 und 4 Finger. Färbe schließlich die Finger 1 und 4 auf dem Bild ein (und nicht deine eigenen Finger, wie es sich anhört).

Meiner Meinung nach ist der Teil mit den Fingern überflüssig und verwirrend. Allerdings ist das Konzept der Zahlenverbindungen viel älter als der CCS. Zahlenbindungen werden im CCS eigentlich nicht erwähnt, obwohl sie mit diesem Standard zusammenhängen:

1.OA.4
Verstehe die Subtraktion als ein unbekanntes Additionsproblem. Subtrahiere zum Beispiel 10 – 8, indem du die Zahl findest, die 10 ergibt, wenn man sie zu 8 addiert.

und mit diesem

1.OA.6.
Addiere und subtrahiere innerhalb von 20 und zeige, dass du Addition und Subtraktion innerhalb von 10 beherrschst.

Ich weiß nicht, warum dieses Arbeitsblatt mit den Zahlenbindungen als Beispiel für Common Core Math angegeben ist. Es wäre viel besser, es als Beispiel für ein schlecht formuliertes Arbeitsblatt zu bezeichnen, das sogar aus der Zeit vor den Common Core stammen KÖNNTE (und in diesem speziellen Lehrplan einfach wiederverwendet wird)… denn wie ich schon sagte, werden Zahlenverbindungen in den CCS NICHT erwähnt.

Was die Common Core Math Standards nicht sind

1. Sie sind keine „neue Mathematik“. Im Vergleich zu vielen Mathematiklehrplänen der 2000er Jahre, die nicht-traditionelle Algorithmen betonten, sind die CCS eine klare Hinwendung zu traditionellen Algorithmen und Auswendiglernen. Sehen Sie sich diese spezifischen Standards an:
   

   2.OA.2
   Fließend addieren und subtrahieren innerhalb von 20 unter Verwendung mentaler Strategien. Bis zum Ende der Klasse 2 alle Summen von zwei einstelligen Zahlen auswendig kennen.
   Anmerkung von Maria: Das sind die grundlegenden Additionsfakten, wie 7 + 7 oder 5 + 4.

   3.OA.7
   Fließend multiplizieren und dividieren innerhalb von 100, unter Verwendung von Strategien wie der Beziehung zwischen Multiplikation und Division (z.B. wenn man weiß, dass 8 × 5 = 40 ist, weiß man auch, dass 40 ÷ 5 = 8 ist) oder Eigenschaften der Operationen. Am Ende der Klasse 3 alle Produkte von zwei einstelligen Zahlen auswendig kennen.
   Anmerkung von Maria: Das bedeutet Multiplikationstabellen und grundlegende Fakten zur Division.

   4.NBT.4
   Mehrstellige ganze Zahlen unter Verwendung des Standardalgorithmus fließend addieren und subtrahieren.

   5.NBT.5
   Mehrstellige ganze Zahlen unter Verwendung des Standardalgorithmus fließend multiplizieren.
   Anmerkung von Maria: Das bedeutet nicht, dass die Schüler nur in der 5. Klasse mehrstellige ganze Zahlen multiplizieren; das wird auch in der 3. und 4.

2. Die Standards schreiben den Lehrern und Schülern keine seltsamen Strategien oder visuellen Modelle vor. Viele Standards überlassen es den Lehrern und Schülern, wie sie vorgehen. Zum Beispiel:
   

   2.NBT.5
   Fließend addieren und subtrahieren innerhalb von 100 unter Verwendung von Strategien, die auf dem Stellenwert, den Eigenschaften der Operationen und/oder der Beziehung zwischen Addition und Subtraktion beruhen.

   Beachten Sie das „und/oder“ im obigen Satz. Das bedeutet, dass die Lehrkräfte und die Schülerinnen und Schüler NICHT auf die Verwendung bestimmter Strategien beschränkt sind und auch nicht aufgefordert werden, mehrere Strategien zu verwenden. Der traditionelle Algorithmus des „Borgens“ ist eine Strategie, die auf dem Stellenwert basiert, daher ist er hier in 2.NBT.5 enthalten.

   2.NBT.9
   Erläutern, warum Additions- und Subtraktionsstrategien funktionieren, indem sie den Stellenwert und die Eigenschaften der Operationen nutzen. Erklärungen können durch Zeichnungen oder Objekte unterstützt werden.

   Es heißt „kann durch Zeichnungen unterstützt werden“, aber es zwingt einen nicht dazu, noch beschränkt es einen auf die Verwendung eines bestimmten visuellen Modells oder einer bestimmten Art von Zeichnung.

   3.OA.3
   Multiplikation und Division innerhalb von 100 anwenden, um Wortaufgaben zu lösen, die gleiche Gruppen, Reihen und Messgrößen einbeziehen, z.B. indem man Zeichnungen und Gleichungen mit einem Symbol für die unbekannte Zahl verwendet, um das Problem darzustellen.

   Der Schüler MUSS keine Zeichnung verwenden. Das wird nur als Möglichkeit erwähnt.

   4.NBT.5
   Multiplizieren Sie eine ganze Zahl mit bis zu vier Ziffern mit einer einstelligen ganzen Zahl und multiplizieren Sie zwei zweistellige Zahlen, indem Sie Strategien verwenden, die auf dem Stellenwert und den Eigenschaften der Operationen basieren. Veranschaulichen und erläutern Sie die Berechnung mit Hilfe von Gleichungen, rechteckigen Feldern und/oder Flächenmodellen.

   Beachten Sie das „und/oder“. Veranschaulichen Sie die Berechnung, aber es reicht aus, sie mit Gleichungen zu veranschaulichen. Sie MÜSSEN sie nicht mit Hilfe von Arrays veranschaulichen.

   In einigen Normen wird ein bestimmtes visuelles Modell erwähnt, z. B. eine Zahlenreihe oder ein rechteckiges Flächenmodell, aber das ist seltener als eine Wahlmöglichkeit wie in den obigen Normen.

Konzeptuelle Mathematik

Es gibt einige Standards, die sich mit der konzeptionellen Seite der Mathematik befassen, die Grundschullehrer möglicherweise nicht verstehen, wenn ihnen nicht beigebracht wird, was sie bedeuten; zum Beispiel:

5. NF.7b
Interpretiere die Division einer ganzen Zahl durch einen Einheitsbruch und berechne solche Quotienten. Zum Beispiel eine Geschichte für 4 ÷ (1/5) erstellen und ein visuelles Bruchmodell verwenden, um den Quotienten zu zeigen. Verwenden Sie die Beziehung zwischen Multiplikation und Division, um zu erklären, dass 4 ÷ (1/5) = 20 ist, weil 20 × (1/5) = 4 ist.

Ein solches Problem könnte sein: Wie viele Stücke, die 1/5-ft lang sind, kann man aus einem 4-ft langen Stück Material ausschneiden? Ein visuelles Modell könnte 4 ganze Stücke zeigen, die in Fünftel unterteilt sind. Man kann dann abzählen, dass 4 Ganzheiten insgesamt 20 Fünftel haben.

5.NF.4b
Bestimme den Flächeninhalt eines Rechtecks mit gebrochenen Seitenlängen, indem du es mit Einheitsquadraten der entsprechenden gebrochenen Seitenlängen überdeckst, und zeige, dass der Flächeninhalt derselbe ist, den man durch Multiplikation der Seitenlängen erhalten würde. Multipliziere gebrochene Seitenlängen, um Flächen von Rechtecken zu finden, und stelle die Bruchprodukte als Rechteckflächen dar.

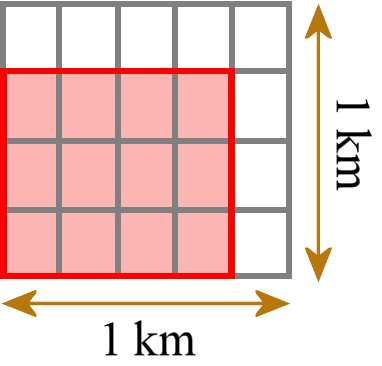Das bedeutet zum Beispiel ein Rechteck mit Seitenlängen von 3/4 km und 4/5 km. Dann kacheln wir es mit kleinen Einheitsrechtecken (nicht Einheitsquadraten; hier hat die Norm selbst die falsche Terminologie), die jeweils 1/4 km und 1/5 km Seitenlänge haben.

Wir können zählen, wie viele kleine Kacheln wir brauchen. Wir brauchen 12 solcher Plättchen. Jedes Plättchen hat eine Fläche von 1/20 km2, also ist die Gesamtfläche 12/20 km2. Dann überprüfen und vergleichen wir, dass wir die gleiche Antwort erhalten, als wenn wir die beiden Seitenlängen mit der normalen Bruchmultiplikation multipliziert hätten (3/4 km × 4/5 km = 12/20 km2).

Ich habe diese Art von Problemen immer in meinen Büchern gehabt – sogar bevor CCS aufkam.

Einige Leute argumentieren, dass Kinder ein solches konzeptionelles Verständnis nicht brauchen oder dass es zu schwierig ist. Ich persönlich bin da anderer Meinung. Ich habe mich immer (auch vor der CCS) bemüht, die Konzepte der Bruchrechnung zu erklären, damit die Schüler nicht „blind den Regeln folgen“ und nur dann mit Brüchen rechnen können, wenn sie sich die Regel richtig merken. Ich habe immer das konzeptionelle Verständnis in der Mathematik betont (wie meine Leser wissen!).

Aber ich hoffe, Sie können verstehen, dass einige dieser Dinge für Lehrer und Eltern ungewohnt sein können, und deshalb ist es kein Wunder, dass es für sie schwierig ist, den Common Core Standards zu folgen.

Ich hoffe, dass die Math Mammoth Light Blue Series und die Einheiten, die ich in meinen Shops Teachers Pay Teachers und Teachers‘ Notebook verkaufe, jenen Lehrern &Eltern helfen können, die an den Common Core angepasste Materialien benötigen. Und wie ich schon sagte, können auch die anderen sie getrost verwenden. Sie enthalten keine „seltsame“ oder unsinnige Mathematik, sondern basieren wie immer auf der soliden Grundlage, die Konzepte der Mathematik zusammen mit den Verfahren zu lehren.

Von Maria Miller