Eigenwerte sind eine spezielle Menge von Skalaren, die mit einem linearen Gleichungssystem (d.e., einer Matrixgleichung), die manchmal auch als charakteristische Wurzeln, charakteristische Werte (Hoffman und Kunze 1971), Eigenwerte oder latente Wurzeln (Marcus und Minc 1988, S. 144) bezeichnet werden.

Die Bestimmung der Eigenwerte und Eigenvektoren eines Systems ist in der Physik und im Ingenieurwesen äußerst wichtig, da sie einer Matrixdiagonalisierung entspricht und in so häufigen Anwendungen wie der Stabilitätsanalyse, der Physik rotierender Körper und kleinen Schwingungen schwingender Systeme vorkommt, um nur einige zu nennen. Jedem Eigenwert ist ein entsprechender so genannter Eigenvektor zugeordnet (oder allgemein ein entsprechender rechter Eigenvektor und ein entsprechender linker Eigenvektor; für Eigenwerte gibt es keine analoge Unterscheidung zwischen links und rechts).

Die Zerlegung einer quadratischen Matrix in Eigenwerte und Eigenvektoren wird in dieser Arbeit als Eigenwertzerlegung bezeichnet, und die Tatsache, dass diese Zerlegung immer möglich ist, solange die aus den Eigenvektoren von bestehende Matrix quadratisch ist, wird als Eigenwertzerlegungssatz bezeichnet.

Der Lanczos-Algorithmus ist ein Algorithmus zur Berechnung der Eigenwerte und Eigenvektoren für große symmetrische dünnbesetzte Matrizen.

Sei eine lineare Transformation, die durch eine Matrix dargestellt wird. Wenn es einen Vektor gibt, so dass

(1)

für einen Skalar , dann heißt der Eigenwert von mit entsprechendem (rechten) Eigenvektor .

Wenn eine quadratische Matrix

(2)

mit Eigenwert ist, dann erfüllen die entsprechenden Eigenvektoren

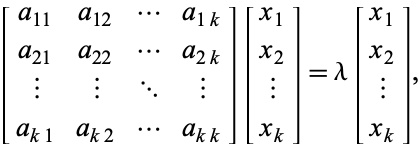(3)

, was äquivalent zum homogenen System

ist

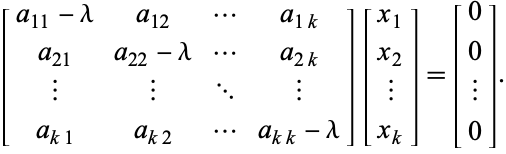(4)

Gleichung (4) kann kompakt geschrieben werden als

(5)

wobei die Identitätsmatrix ist. Wie in der Cramerschen Regel gezeigt, hat ein lineares Gleichungssystem nicht-triviale Lösungen, wenn die Determinante verschwindet, Die Lösungen von Gleichung (5) sind also gegeben durch

(6)

Diese Gleichung ist bekannt als die charakteristische Gleichung von , und die linke Seite ist bekannt als das charakteristische Polynom.

Zum Beispiel für eine Matrix, die Eigenwerte

(7)

, die sich als Lösungen der Charakteristikumsgleichung

(8)

Wenn alle Eigenwerte verschieden sind, dann ergibt das Einsetzen dieser Gleichungen unabhängige Gleichungen für die Komponenten jedes entsprechenden Eigenvektors, und man sagt, das System sei nicht entartet. Wenn die Eigenwerte -fach entartet sind, wird das System als entartet bezeichnet und die Eigenvektoren sind nicht linear unabhängig. In solchen Fällen kann die zusätzliche Bedingung, dass die Eigenvektoren orthogonal sind,

(9)

wobei das Kronecker-Delta ist, angewendet werden, um zusätzliche Bedingungen zu erhalten, die eine Lösung für die Eigenvektoren ermöglichen.

Eigenwerte können in der Wolfram Language mit Eigenwerte berechnet werden. Eigenvektoren und Eigenwerte können mit dem Befehl Eigensystem gemeinsam zurückgegeben werden.

Angenommen, wir kennen den Eigenwert für

(10)

Wir addieren eine Konstante mal die Identitätsmatrix zu ,

(11)

so dass die neuen Eigenwerte gleich den alten plus sind. Durch Multiplikation von mit einer Konstanten

(12)

sind die neuen Eigenwerte die alten multipliziert mit .

Betrachten wir nun eine Ähnlichkeitstransformation von . Sei die Determinante von , dann

			(13)
			(14)
			(15)

die Eigenwerte sind also die gleichen wie für .