Stellt euch ein Quadrat Papier vor, das flach auf eurem Schreibtisch liegt. Ich bitte Sie, Ihre Augen zu schließen. Sie hören, wie sich das Papier bewegt. Wenn Sie die Augen öffnen, scheint sich das Papier nicht verändert zu haben. Was könnte ich damit gemacht haben, während Sie nicht hingesehen haben?

Es ist offensichtlich, dass ich das Papier nicht um 30 Grad gedreht habe, denn dann würde es anders aussehen.

Ich habe es auch nicht über eine Linie umgedreht, die, sagen wir, eine der Ecken mit dem Mittelpunkt einer anderen Kante verbindet. Das Papier würde anders aussehen, wenn ich das getan hätte.

Was ich jedoch hätte tun können, war, das Papier im oder gegen den Uhrzeigersinn um ein beliebiges Vielfaches von 90 Grad zu drehen oder es über eine der diagonalen Linien oder die horizontalen und vertikalen Linien zu kippen.

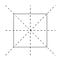
Eine hilfreiche Art, die Transformationen zu visualisieren, ist es, die Ecken des Quadrats zu markieren.

Die letzte Möglichkeit ist die, nichts zu tun. Dies nennt man die Identitätstransformation. Alle diese Möglichkeiten zusammen werden Symmetrietransformationen des Quadrats genannt.

Ich kann Symmetrietransformationen kombinieren, um andere Symmetrietransformationen zu machen. Zum Beispiel ergeben zwei Umdrehungen um das Liniensegment BD die Identität, ebenso wie vier aufeinanderfolgende Drehungen um 90 Grad gegen den Uhrzeigersinn. Eine Umdrehung um die vertikale Linie, gefolgt von einer Umdrehung um die horizontale Linie, hat den gleichen Effekt wie eine Drehung um 180 Grad. Allgemein gilt, dass jede Kombination von Symmetrietransformationen eine Symmetrietransformation ergibt. Die folgende Tabelle enthält die Regeln für die Zusammensetzung von Symmetrietransformationen:

In dieser Tabelle bezeichnen R mit den Indizes 90, 180 und 270 Drehungen gegen den Uhrzeigersinn um 90, 180 und 270 Grad, H bedeutet eine Drehung um die horizontale Linie, V eine Drehung um die vertikale Linie, MD eine Drehung um die Diagonale von links oben nach rechts unten und OD eine Drehung über die andere Diagonale. Um das Produkt von A und B zu finden, geht man in die Zeile von A und dann in die Spalte von B. Zum Beispiel: H∘MD=R₉₀.

Es gibt ein paar Dinge, die du vielleicht bemerkst, wenn du dir die Tabelle ansiehst:

• Die Operation ∘ ist assoziativ, was bedeutet, dass A∘(B∘C) = (A∘B)∘C für beliebige Transformationen A, B und C.
• Für jedes Paar von Symmetrietransformationen A und B ist die Komposition A∘B ebenfalls eine Symmetrietransformation
• Es gibt ein Element e, so dass A∘e=e∘A für jedes A
• Für jede Symmetrietransformation A, gibt es eine einzige Symmetrietransformation A-¹, so dass A∘A-¹=A-¹∘A=e

Wir sagen daher, dass die Sammlung der Symmetrietransformationen eines Quadrats in Verbindung mit der Komposition eine mathematische Struktur bildet, die wir Gruppe nennen. Diese Gruppe wird als D₄ bezeichnet, als Dihedralgruppe für das Quadrat. Diese Strukturen sind Gegenstand dieses Artikels.

Definition einer Gruppe

Eine Gruppe ⟨G,*⟩ ist eine Menge G mit einer Regel * für die Kombination zweier beliebiger Elemente in G, die die Gruppenaxiome erfüllt:

In der Zusammenfassung unterdrücken wir oft * und schreiben a*b als ab und bezeichnen * als Multiplikation.

Es ist nicht notwendig, dass * kommutativ ist, was bedeutet, dass a*b=b*a. Das sieht man an der Tabelle von D₄, wo H∘MD=R₉₀ aber MD∘H=R₂₇₀. Gruppen, bei denen * kommutativ ist, nennt man nach Neils Abel abelsche Gruppen.

Abelsche Gruppen sind eher die Ausnahme als die Regel. Ein weiteres Beispiel für eine nichtabelsche Gruppe sind die Symmetrietransformationen eines Würfels. Man betrachte nur Drehungen um die Achsen:

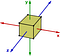
Wenn ich zuerst 90 Grad gegen den Uhrzeigersinn um die y-Achse und dann 90 Grad gegen den Uhrzeigersinn um die z-Achse drehe, dann wird er ein anderes Ergebnis haben, als wenn ich 90 Grad um die z-Achse und dann 90 Grad um die y-Achse drehe.

Es ist möglich, dass ein Element sein eigenes Inverses ist. Betrachten wir die Gruppe, die aus 0 und 1 mit der Operation der binären Addition besteht. Ihre Tabelle lautet:

Die 1 ist eindeutig ihr eigenes Inverses. Auch dies ist eine abelsche Gruppe. Keine Sorge, die meisten Gruppen sind nicht so langweilig.

Weitere Beispiele für Gruppen sind:

• Die Menge der ganzen Zahlen mit Addition.
• Die Menge der rationalen Zahlen ohne 0 mit Multiplikation.
• Die Menge der Lösungen der Polynomgleichung xⁿ-1=0, genannt die n-ten Wurzeln der Einheit, mit Multiplikation.

Hier sind einige Beispiele, die keine Gruppen sind:

• Die Menge der natürlichen Zahlen unter Addition ist keine Gruppe, weil es keine Inversen gibt, was die negativen Zahlen wären.
• Die Menge aller rationalen Zahlen einschließlich 0 mit Multiplikation ist keine Gruppe, weil es keine rationale Zahl q gibt, für die 0/q=1 ist, also nicht jedes Element eine Inverse hat.

Gruppenstruktur

Eine Gruppe ist viel mehr als nur ein Fleck, der die vier Axiome erfüllt. Eine Gruppe kann eine innere Struktur haben, und diese Struktur kann sehr kompliziert sein. Eines der grundlegenden Probleme in der abstrakten Algebra besteht darin, zu bestimmen, wie die innere Struktur einer Gruppe aussieht, denn in der realen Welt sind die Gruppen, die tatsächlich untersucht werden, viel größer und komplizierter als die einfachen Beispiele, die wir hier gegeben haben.

Eine der grundlegenden Arten der inneren Struktur ist eine Untergruppe. Eine Gruppe G hat eine Untergruppe H, wenn H eine Teilmenge von G ist und:

• Für a,b∈H, a*b∈H und b*a∈H
• Für a∈H, a-¹∈H
• Die Identität ist ein Element von H

Wenn H≠G, dann sagt man, dass H eine echte Untergruppe ist. Die Untergruppe von G, die nur aus der Identität besteht, heißt triviale Untergruppe.

Eine nichtabelsche Gruppe kann kommutative Untergruppen haben. Betrachten wir die quadratische Dihedralgruppe, die wir in der Einleitung besprochen haben. Diese Gruppe ist nicht abelsch, aber die Untergruppe der Rotationen ist abelsch und zyklisch:

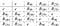
Wir geben nun zwei Beispiele für die Gruppenstruktur.

Auch wenn eine Gruppe G nicht abelsch ist, kann es sein, dass es eine Sammlung von Elementen von G gibt, die mit allen Elementen von G übereinstimmen. Diese Sammlung wird Zentrum von G genannt. Das Zentrum C ist eine Untergruppe von G. Beweis:

Nehmen wir nun an, dass f eine Funktion ist, deren Gebiet und Bereich beide G sind. Eine Periode von f ist ein Element a∈G, so dass f(x)=f(ax) für alle x∈G. Die Menge P der Perioden von f ist eine Untergruppe von G. Beweis:

Finite Gruppen sind endlich erzeugt

Wir haben gesehen, dass zyklische Gruppen durch ein einziges Element erzeugt werden. Wenn es möglich ist, jedes Element einer Gruppe G als Produkt einer (nicht notwendigerweise richtigen) Teilmenge A von G zu schreiben, dann sagen wir, dass A G generiert und schreiben dies als G=⟨A⟩. Der einfachste Beweis, den du je sehen wirst, ist der Beweis, dass alle endlichen Gruppen von einer endlichen Erzeugenden Menge erzeugt werden:

• Lass G endlich sein. Jedes Element von G ist ein Produkt von zwei anderen Elementen von G, also ist G=⟨G⟩. QED.

Wir werden diesen Artikel mit einer Anwendung abschließen.

Fehlerresistente Kommunikation

Die einfachste Art, digitale Informationen zu übertragen, ist, sie in binäre Zeichenketten fester Länge zu kodieren. Kein Kommunikationsverfahren ist völlig frei von Störungen, so dass immer die Möglichkeit besteht, dass die falschen Daten empfangen werden. Die Methode der Maximalwahrscheinlichkeitsdekodierung ist ein einfacher und effektiver Ansatz zur Erkennung und Korrektur von Übertragungsfehlern.

Bei 𝔹ⁿ handelt es sich um die Menge der binären Zeichenketten oder Wörter der Länge n. Es ist einfach zu zeigen, dass 𝔹ⁿ eine abelsche Gruppe unter binärer Addition ohne Übertrag ist (so dass zum Beispiel 010+011=001). Man beachte, dass jedes Element sein eigenes Inverses ist. Ein Code C ist eine Teilmenge von 𝔹ⁿ. Es folgt ein Beispiel für einen Code in 𝔹⁶:

C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}

Die Elemente eines Codes werden Codewörter genannt. Es werden nur Codewörter übertragen. Von einem Fehler spricht man, wenn eine Störung ein Bit in einem übertragenen Wort verändert. Der Abstand d(a,b) zwischen zwei Codewörtern a und b ist die Anzahl der Ziffern, in denen sich zwei Codewörter unterscheiden. Der Mindestabstand eines Codes ist der kleinste Abstand zwischen zwei beliebigen Codewörtern. Für den obigen Beispielcode beträgt der Mindestabstand drei.

Bei der Methode der Maximalwahrscheinlichkeitsdekodierung sollte der Empfänger, wenn er ein Wort x empfängt, das Fehler enthalten kann, x als das Codewort a interpretieren, so dass d(a,x) ein Minimum ist. Ich werde zeigen, dass dies für einen Code der minimalen Distanz m immer (1) Fehler erkennen kann, die weniger als m Bits verändern und (2) Fehler korrigieren kann, die ½(m-1) oder weniger Bits verändern.

In unserem Beispielcode ist m=3 und die Kugel mit Radius ½(m-1)=1 um das Codewort 011101 ist {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Wenn der Empfänger also eines dieser Wörter empfängt, weiß er, dass er eigentlich 011101 empfangen sollte.

Das ist ja alles schön und gut, aber was hat das alles mit der Gruppentheorie zu tun? Die Antwort liegt darin, wie wir die Codes erzeugen, mit denen diese Methode arbeitet.

Es ist möglich, dass ein Code in 𝔹ⁿ eine Untergruppe bildet. In diesem Fall sagen wir, dass der Code ein Gruppencode ist. Gruppencodes sind endliche Gruppen, sie sind also endlich erzeugt. Wir werden sehen, wie man einen Code erzeugt, indem man eine erzeugende Menge findet.

Ein Code kann so spezifiziert werden, dass die ersten paar Bits jedes Codeworts die Informationsbits und die Bits am Ende die Paritätsbits genannt werden. In unserem Beispielcode C sind die ersten drei Bits die Informationsbits und die letzten drei die Paritätsbits. Die Paritätsbits erfüllen die Gleichungen für die Paritätsprüfung. Für ein Codewort A₁A₂A₃A₄A₅A₆ lauten die Paritätsgleichungen A₄=A₁+A₂, A₅=A₂+A₃, und A₆=A₁+A₃. Paritätsgleichungen bieten einen weiteren Schutz vor Fehlern: Wenn eine der Paritätsgleichungen nicht erfüllt ist, ist ein Fehler aufgetreten.

Wir gehen folgendermaßen vor. Angenommen, wir wollen Codewörter mit m Informationsbits und n Paritätsbits. Um einen Gruppencode zu erzeugen, schreibt man eine Matrix mit m Zeilen und m+n Spalten. In den Block, der von den ersten m Spalten gebildet wird, schreiben Sie die m×m-Identitätsmatrix. Schreibe in Spalte j für m+1≤j≤m_n eine 1 in die k-te Zeile, wenn Aₖ in der Paritätsgleichung für das Paritätsbit Aⱼ auftaucht, und sonst 0. In unserem Beispielcode lautet die Matrix:

Eine solche Matrix wird als generierende Matrix für den Gruppencode bezeichnet. Man kann direkt beweisen, dass die Zeilen C erzeugen:

Die Zeilen einer beliebigen erzeugenden Matrix bilden eine erzeugende Menge für einen Gruppencode C. Beweis:

• Identität und Inverse: Jede Zeile, die zu sich selbst addiert wird, ergibt die Identität, eine Kette, die aus allen Nullen besteht.
• Schluss: Wenn A,B∈C dann sind A und B Summen von Zeilen der erzeugenden Matrix, also ist A+B auch eine Summe von Zeilen der erzeugenden Matrix. Daher ist A+B∈C.

Damit können wir einen Code erzeugen, jetzt werde ich zeigen, wie man einen nützlichen Code erzeugt.

Definiere das Gewicht w(x) als die Anzahl der Einsen in x. Zum Beispiel w(100101)=3. Es ist offensichtlich, dass w(x)=d(x,0) ist, wobei 0 ein Wort ist, dessen Ziffern alle Nullen sind. Das Mindestgewicht W eines Codes ist das Gewicht des Codeworts mit den wenigsten Nullen im Code. Für einen Code mit der Mindestdistanz m ist d(x,0)≥m, also w(x)≥m und somit W=m.

Erinnern wir uns daran, dass ein Wort eine Reihe von Paritätsprüfungsgleichungen erfüllen muss, um als Codewort zu gelten. Für unseren Beispielcode sind dies A₄=A₁+A₂, A₅=A₂+A₃, und A₆=A₁+A₃. Wir können diese auch als lineares System schreiben:

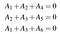
Was wiederum in Form von Punktprodukten geschrieben werden kann:

Oder in kompakterer Form als Ha=0, wobei a=(A₁,A₂,A₃,A₄,A₅,A₆) und H die Paritätsprüfungsmatrix für den Code ist:

Man kann durch direkte Berechnung überprüfen, dass, wenn w(a)≤2 ist, wir nicht Ha=0 haben können. Im Allgemeinen ist das minimale Gewicht t+1, wobei t die kleinste Zahl ist, bei der eine beliebige Sammlung von t Spalten von H sich nicht zu Null summiert (d.h. sie sind linear unabhängig). Dies zu beweisen, würde uns ein wenig zu weit in die lineare Algebra führen.

Wenn Sie das erschreckt, machen Sie sich keine Sorgen. Wir können einige sehr gute Codes ohne sie erzeugen, indem wir die Tatsache ausnutzen, dass das Ergebnis, das ich gerade erwähnt habe, impliziert, dass, wenn jede Spalte von H ungleich Null ist und keine zwei Spalten gleich sind, das Mindestgewicht und damit der Mindestabstand des Codes mindestens drei ist. Das ist sehr gut: Wenn man davon ausgeht, dass in unserem Kommunikationssystem pro hundert übertragenen Wörtern ein Bitfehler auftritt, dann wird nur eines von zehntausend übertragenen Wörtern einen unkorrigierten Fehler aufweisen und eines von einer Million übertragenen Wörtern einen unerkannten Fehler.

So haben wir jetzt ein Rezept, um einen nützlichen Code für das Maximum-Likelihood-Detektionsschema für Codewörter zu erzeugen, die m Informationsbits und n Paritätsbits enthalten:

• Erstelle eine Matrix mit m+n Spalten und n Zeilen. Füllen Sie die Matrix mit Einsen und Nullen auf, so dass keine zwei Spalten gleich sind und keine Spalte nur aus Nullen besteht.
• Jede Zeile der resultierenden Paritätsprüfungsmatrix entspricht einer der Paritätsbitgleichungen. Schreibe sie als Gleichungssystem und löse sie so, dass jedes Paritätsbit in Form der Informationsbits geschrieben wird.
• Erstelle eine Matrix mit m+n Spalten und m Zeilen. Schreibe in den Block, der von den ersten m Spalten gebildet wird, die m×m-Identitätsmatrix. In Spalte j für m+1≤j≤m_n schreibe in die k-te Zeile eine 1, wenn Aₖ in der Paritätsgleichung für das Paritätsbit Aⱼ erscheint, und sonst 0.
• Die Zeilen dieser Matrix sind die Generatoren einer Codegruppe mit einem Mindestabstand von drei. Dies ist der Code, den wir verwenden werden.

Angenommen, ich benötige einen einfachen Code mit acht Wörtern und brauche nur eine einfache Fehlererkennung und keine Korrektur, so dass ich mit einem Mindestabstand von zwei auskomme. Ich brauche drei Informationsbits und zwei Paritätsbits. Ich schreibe die folgende Paritätsprüfungsmatrix auf:

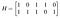
Es gibt zwei Paare von Spalten, die gleich sind, so dass das kleinste t, für das jede Sammlung von t Spalten linear unabhängig ist, eins ist, so dass das Mindestgewicht und damit der Mindestabstand, den ich haben werde, zwei ist. Die Zeilen stellen die Paritätsprüfungsgleichungen A₄=A₁+A₃ und A₅=A₁+A₂+A₃ dar. Meine Erzeugungsmatrix lautet also:

Und die Zeilen dieser Matrix erzeugen die Codegruppe:

• {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}

Abschließende Bemerkungen

Abstrakte Algebra ist ein tiefes Thema mit weitreichenden Auswirkungen, aber es ist auch sehr leicht zu erlernen. Abgesehen von ein paar beiläufigen Erwähnungen der linearen Algebra ist fast alles, was ich hier besprochen habe, auch für jemanden zugänglich, der nur Algebra in der Schule hatte.

Als ich die Idee hatte, diesen Artikel zu schreiben, wollte ich eigentlich über den Rubik-Würfel sprechen, aber schließlich wollte ich ein Beispiel wählen, das nur mit den grundlegendsten Ideen der Gruppentheorie behandelt werden kann. Außerdem gibt es so viel über die Gruppe des Rubik-Würfels zu sagen, dass sie einen eigenständigen Artikel verdient, der also bald erscheinen wird.

Meine College-Kurse in abstrakter Algebra basierten auf dem Buch A Book of Abstract Algebra von Charles Pinter, das eine leicht verständliche Abhandlung ist. Die Beispiele in diesem Artikel wurden alle mit einigen Modifikationen von Pinter übernommen.

Als letzter Hinweis: Alle Bilder, die nicht zitiert werden, sind meine eigenen Originalarbeiten und können mit Quellenangabe verwendet werden. Wie immer freue ich mich über Korrekturen oder Anfragen zur Klarstellung.