Wie der P-Only-Regler berechnet der Proportional-Integral (PI)-Algorithmus ein Reglerausgangssignal (CO) und sendet es zu jeder Abtastzeit T an das Stellglied (z. B. Ventil, drehzahlgeregelte Pumpe). Der vom PI-Algorithmus berechnete CO-Wert wird von den Einstellparametern des Reglers und der Regelabweichung e(t) beeinflusst.
PI-Regler haben zwei Einstellparameter, die angepasst werden müssen. Dadurch sind sie zwar schwieriger einzustellen als ein reiner P-Regler, aber nicht so komplex wie ein PID-Regler mit drei Parametern.
Durch die integrale Wirkung können PI-Regler die Regelabweichung eliminieren, eine große Schwäche eines reinen P-Reglers. Somit bieten PI-Regler ein ausgewogenes Verhältnis von Komplexität und Leistungsfähigkeit, das sie zum weitaus am häufigsten verwendeten Algorithmus in der Prozesssteuerung macht.
Der PI-Algorithmus
Während verschiedene Hersteller den im Wesentlichen gleichen Algorithmus in verschiedenen Formen darstellen, untersuchen wir hier das, was unterschiedlich als die abhängige, ideale, kontinuierliche, Positionsform beschrieben wird:
![]()
Wobei:
CO = Reglerausgangssignal (der Drahtausgang)
CObias = Regler-Vorspannung oder Nullwert; eingestellt durch stoßfreie Übertragung, wie unten erläutert
e(t) = aktueller Reglerfehler, definiert als SP – PV
SP = Sollwert
PV = gemessene Prozessvariable (der Draht nach innen)
Kc = Reglerverstärkung, ein Abstimmungsparameter
Ti = Nachstellzeit, ein Abstimmungsparameter
Die ersten beiden Begriffe rechts vom Gleichheitszeichen sind identisch mit dem oben in diesem Artikel erwähnten P-Only-Regler.
Der Integralmodus des Reglers ist der letzte Term der Gleichung. Seine Funktion besteht darin, die Regelabweichung e(t) über die Zeit zu integrieren oder kontinuierlich zu summieren.
Einige Dinge, die wir über den Abstimmparameter Ti für die Nachstellzeit wissen sollten:
| ▪ | Er verleiht dem Integralanteil ein separates Gewicht, so dass der Einfluss der Integralwirkung unabhängig eingestellt werden kann. |
| ▪ | Sie steht im Nenner, so dass kleinere Werte dem integralen Term ein größeres Gewicht verleihen (d. h. |
| ▪ | Er hat Zeiteinheiten und ist daher immer positiv. |
Funktion des Proportionalanteils
Wie beim reinen P-Regler addiert oder subtrahiert der Proportionalanteil des PI-Reglers, Kc-e(t), zu CObias auf der Grundlage der Größe der Regelabweichung e(t) zu jedem Zeitpunkt t.
Wenn e(t) wächst oder schrumpft, wächst oder schrumpft der zu CObias hinzugefügte Betrag sofort und proportional. Die Vorgeschichte und der aktuelle Verlauf der Regelabweichung haben keinen Einfluss auf die Berechnung des proportionalen Terms.
Das nachstehende Diagramm (für eine Großansicht anklicken) veranschaulicht diese Idee für eine Sollwertreaktion. Die in der Proportionalberechnung verwendete Regelabweichung ist im Diagramm dargestellt:
▪ Zum Zeitpunkt t = 25 min, e(25) = 60-56 = 4
▪ Zum Zeitpunkt t = 40 min, e(40) = 60-62 = -2
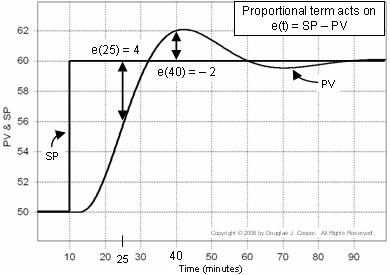
Wenn man bedenkt, dass die Regelabweichung e(t) = SP – PV ist, kann man, anstatt PV und SP wie oben als getrennte Kurven zu betrachten, e(t) zu jedem Zeitpunkt t berechnen und darstellen.
Unten (zum Vergrößern anklicken) sehen Sie die gleichen Daten wie oben, nur dass sie als Diagramm von e(t) selbst dargestellt sind. Beachten Sie, dass im obigen Diagramm PV = SP = 50 für die ersten 10 Minuten ist, während im Fehlerdiagramm unten e(t) = 0 für denselben Zeitraum ist.
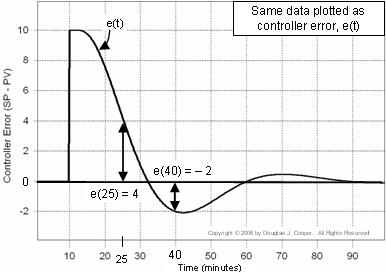
Dieses Diagramm ist nützlich, da es uns hilft, zu visualisieren, wie der Fehler des Reglers kontinuierlich Größe und Vorzeichen im Laufe der Zeit ändert.
Funktion des Integralbegriffs
Während der Proportionalbegriff die aktuelle Größe von e(t) nur zum Zeitpunkt der Reglerberechnung berücksichtigt, berücksichtigt der Integralbegriff die Historie des Fehlers oder wie lange und wie weit die gemessene Prozessvariable im Laufe der Zeit vom Sollwert abgewichen ist.
Integration ist eine kontinuierliche Summierung. Integration der Regelabweichung über die Zeit bedeutet, dass wir die gesamte Regelabweichungshistorie bis zum aktuellen Zeitpunkt aufsummieren, beginnend mit der ersten Umschaltung des Reglers auf Automatik.
Regelabweichung ist e(t) = SP – PV. In der nachstehenden Grafik (zum Vergrößern anklicken) wird die Integralsumme des Fehlers als die schattierten Flächen zwischen den SP- und PV-Kurven berechnet.
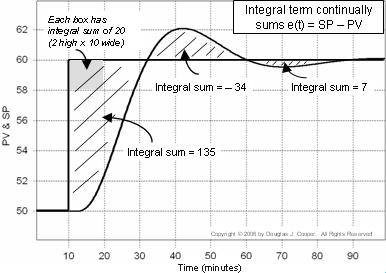
Jedes Kästchen in der Grafik hat eine Integralsumme von 20 (2 hoch x 10 breit). Wenn wir die Anzahl der Kästchen (einschließlich der Bruchteile von Kästchen) zählen, die in den schattierten Bereichen enthalten sind, können wir die Integralsumme des Fehlers berechnen.
Wenn also die PV den Sollwert zum ersten Mal um t = 32 überschreitet, ist die Integralsumme auf etwa 135 angewachsen. Wir schreiben den Integralterm des PI-Reglers wie folgt:
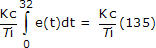
Da der Fehler des Reglers für die Berechnung ausschlaggebend ist, können wir die Situation anhand eines Fehlerdiagramms des Reglers direkt ablesen (klicken Sie für eine größere Ansicht):

Beachten Sie, dass das Integral jedes schattierten Abschnitts dasselbe Vorzeichen wie der Fehler hat. Da sich die Integralsumme zu akkumulieren beginnt, wenn der Regler zum ersten Mal in den Automatikbetrieb übergeht, wächst die gesamte Integralsumme, solange e(t) positiv ist, und schrumpft, wenn sie negativ ist.
Zum Zeitpunkt t = 60 min auf den Diagrammen ist die Integralsumme 135 – 34 = 101. Die Reaktion ist zum Zeitpunkt t = 90 min weitgehend abgeschlossen, und die Integralsumme beträgt dann 135 – 34 + 7 = 108.
Integrale Aktion eliminiert Offset
Der vorherige Satz enthält eine subtile, aber sehr wichtige Beobachtung. Die Antwort ist zum Zeitpunkt t = 90 min weitgehend vollständig, doch die integrale Summe aller Fehler ist nicht Null.
In diesem Beispiel hat die integrale Summe einen End- oder Restwert von 108. Dieser Restwert ermöglicht die integrale Wirkung des PI-Reglers, um den Offset zu eliminieren.
Wie in einem früheren Artikel besprochen, tritt bei den meisten Prozessen mit reiner P-Regelung während des normalen Betriebs ein Offset auf. Der Offset ist ein dauerhafter Wert für den Reglerfehler (d.h. PV ist im eingeschwungenen Zustand nicht gleich SP).
Aus dem P-Only-Regler erkennen wir:
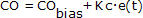
dass CO immer gleich CObias ist, es sei denn, wir addieren oder subtrahieren etwas dazu.
Die einzige Möglichkeit, etwas zu CObias in der obigen P-Only-Gleichung zu addieren oder zu subtrahieren, ist, wenn e(t) nicht Null ist. Wenn e(t) nicht konstant Null ist, dann ist PV nicht gleich SP und wir haben einen Offset.
Mit dem PI-Regler:
![]()
wissen wir nun, dass die integrale Fehlersumme einen End- oder Restwert haben kann, nachdem eine Reaktion abgeschlossen ist. Das ist wichtig, weil es bedeutet, dass e(t) Null sein kann, wir aber immer noch etwas haben können, das wir zu CObias addieren oder subtrahieren können, um den endgültigen Reglerausgang, CO, zu bilden.
Solange es also einen Fehler gibt (solange e(t) nicht Null ist), wird der integrale Term wachsen oder schrumpfen, um CO zu beeinflussen. Die Änderungen in CO hören erst auf, wenn PV über einen längeren Zeitraum gleich SP ist (wenn e(t) = 0).
An diesem Punkt kann der Integralterm einen Restwert haben, wie gerade besprochen. Dieser Restwert aus der Integration, wenn er zu CObias addiert wird, erzeugt im Wesentlichen einen neuen Gesamtvorspannungswert, der dem neuen Betriebsniveau entspricht.
In der Tat setzt die Integralwirkung den Vorspannungswert kontinuierlich zurück, um den Offset zu eliminieren, wenn sich das Betriebsniveau ändert.
Herausforderungen der PI-Regelung
Es gibt Herausforderungen bei der Anwendung des PI-Algorithmus:
| ▪ | Die beiden Abstimmungsparameter stehen in Wechselwirkung zueinander und ihr Einfluss muss vom Konstrukteur ausgeglichen werden. |
| ▪ | Der integrale Term neigt dazu, das oszillierende oder rollende Verhalten der Prozessreaktion zu verstärken. |
Da die beiden Abstimmungsparameter miteinander interagieren, kann es eine Herausforderung sein, die „besten“ Abstimmungswerte zu finden. Der Wert und die Bedeutung unseres Entwurfs und des Abstimmungsrezepts nimmt zu, je komplexer der Regler wird.
Initialisierung des Reglers für stoßfreie Übertragung
Wenn wir einen Regler vom Handbetrieb in den Automatikbetrieb (vom offenen Regelkreis in den geschlossenen Regelkreis) umschalten, soll das Ergebnis ereignislos sein. Das heißt, wir wollen nicht, dass die Umschaltung abrupte Steuerungsaktionen verursacht, die unseren Prozess beeinflussen oder stören
Wir erreichen dieses gewünschte Ergebnis bei der Umschaltung, indem wir die Integralfehlersumme des Reglers auf Null initialisieren. Außerdem werden der Sollwert und der Vorspannungswert des Reglers initialisiert, indem wir Folgendes einstellen:
▪ SP gleich dem aktuellen PV
▪ CObias gleich dem aktuellen CO
Wenn die integrale Fehlersumme auf Null gesetzt wird, gibt es nichts, was zu CObias addiert oder subtrahiert werden kann und eine plötzliche Änderung des aktuellen Reglerausgangs verursachen würde. Wenn der Sollwert gleich der gemessenen Prozessvariablen ist, gibt es keinen Fehler, der eine Änderung unseres CO verursacht. Und da die Vorspannung des Reglers auf den aktuellen CO-Wert eingestellt ist, sind wir standardmäßig darauf vorbereitet, den aktuellen Betrieb aufrechtzuerhalten.
Wenn wir also vom Handbetrieb in den Automatikbetrieb wechseln, haben wir einen „stoßfreien Übergang“ ohne Überraschungen. Das ist ein Ergebnis, das jeder zu schätzen weiß.
Rückstellzeit versus Rückstellrate
Die verschiedenen Hersteller gestalten ihre Regelalgorithmen in leicht unterschiedlicher Form. Einige verwenden den Proportionalbereich anstelle der Reglerverstärkung. Einige verwenden auch die Nachstellrate Tr anstelle der Nachstellzeit. Diese sind einfach der Kehrwert voneinander:
Tr = 1/Ti
Unabhängig davon, wie die Abstimmungsparameter ausgedrückt werden, sind die PI-Algorithmen alle gleich gut geeignet.
Es ist jedoch wichtig, dass Sie Ihren Hersteller kennen, bevor Sie mit der Abstimmung Ihres Reglers beginnen, da die Parameterwerte an Ihre spezielle Algorithmusform angepasst werden müssen.Kommerzielle Software für den Entwurf und die Abstimmung von Reglern wird dieses Problem automatisch für Sie lösen.
Implementierung eines PI-Reglers
Wir befassen uns in diesem Artikel mit dem Entwurf, der Abstimmung und der Implementierung von PI-Reglern für den Wärmetauscher und die durch Schwerkraft entleerten Behälter.