Die Euler’sche Identität scheint verblüffend:

Sie ergibt sich aus einer allgemeineren Formel:

Yowza — wir setzen einen imaginären Exponenten in Beziehung zu Sinus und Kosinus! Und irgendwie ergibt das Einsetzen von pi -1? Kann das jemals intuitiv sein?

Nicht laut dem Mathematiker Benjamin Peirce aus dem 19. Jahrhundert:

Es ist absolut paradox; wir können es nicht verstehen, und wir wissen nicht, was es bedeutet, aber wir haben es bewiesen, und deshalb wissen wir, dass es die Wahrheit sein muss.

Argh, diese Einstellung bringt mein Blut zum Kochen! Formeln sind keine magischen Zaubersprüche, die man auswendig lernen kann: wir müssen, müssen, müssen eine Erkenntnis finden. Hier ist meine:

Die Eulersche Formel beschreibt zwei gleichwertige Möglichkeiten, sich im Kreis zu bewegen.

Das ist alles? Bei dieser verblüffenden Gleichung geht es um die Bewegung im Kreis? Ja – und wir können sie verstehen, indem wir auf ein paar Analogien aufbauen:

• Betrachten Sie die Multiplikation mit der Zahl 1 als eine Transformation, die die Zahl verändert: $1 \cdot e^{i \pi}$
• Regelmäßiges exponentielles Wachstum erhöht 1 kontinuierlich um eine bestimmte Rate für eine bestimmte Zeitspanne; imaginäres exponentielles Wachstum dreht 1 kontinuierlich für eine gewisse Zeit
• Wachsen für „pi“ Zeiteinheiten bedeutet, dass man pi Radiant um einen Kreis geht
• Daher bedeutet $e^{i \pi}$, dass man bei 1 anfängt und pi dreht (auf halbem Weg um einen Kreis), um auf -1 zu kommen

Das ist die übergeordnete Sichtweise, lassen Sie uns in die Details gehen. Übrigens, wenn jemand versucht, dich mit $e^{i \pi} = -1$ zu beeindrucken, frag ihn nach i hoch i. Wenn sie es nicht durchdenken können, ist die Eulersche Formel für sie immer noch ein Zauberspruch.

Aktualisierung: Beim Schreiben dachte ich, dass ein Video helfen könnte, die Ideen klarer zu erklären:

Verstehen von cos(x) + i * sin(x)

Das Gleichheitszeichen ist überladen. Manchmal heißt es „setze eine Sache zu einer anderen“ (z.B. x = 3) und manchmal heißt es „diese beiden Dinge beschreiben dasselbe Konzept“ (z.B. $\sqrt{-1} = i$).

Die Eulersche Formel ist letzteres: sie gibt zwei Formeln an, die erklären, wie man sich auf einem Kreis bewegt. Wenn wir die Kreisbewegung mit Hilfe der Trigonometrie untersuchen und x Bogenmaß zurücklegen:

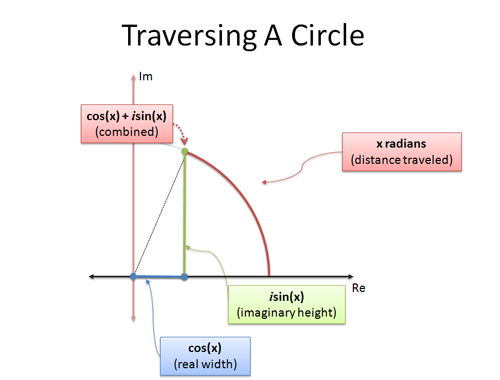
• cos(x) ist die x-Koordinate (horizontaler Abstand)
• sin(x) ist die y-Koordinate (vertikaler Abstand)

Die Aussage

ist eine geschickte Art, die x- und y-Koordinaten in eine einzige Zahl zu zerlegen. Die Analogie „Komplexe Zahlen sind 2-dimensional“ hilft uns, eine einzelne komplexe Zahl als eine Position auf einem Kreis zu interpretieren.

Wenn wir x auf $\pi$ setzen, bewegen wir uns $\pi$ Einheiten entlang der Außenseite des Einheitskreises. Da der Gesamtumfang $2\pi$ beträgt, ist der einfache alte $\pi$ auf halber Strecke und wir befinden uns bei -1.

Neato: Die rechte Seite der Eulerschen Formel ($\cos(x) + i \sin(x)$) beschreibt die Kreisbewegung mit imaginären Zahlen. Nun wollen wir herausfinden, wie die e-Seite der Gleichung dies bewerkstelligt.

Was ist imaginäres Wachstum?

Die Kombination von x- und y-Koordinaten zu einer komplexen Zahl ist knifflig, aber machbar. Aber was bedeutet ein imaginärer Exponent?

Lassen Sie uns einen Schritt zurückgehen. Wenn ich $3^4$ sehe, stelle ich mir das folgendermaßen vor:

• 3 ist das Endergebnis des sofortigen Wachstums (mit e) mit einer Rate von ln(3). Mit anderen Worten: $3 = e^{\ln(3)}$
• $3^4$ ist dasselbe, als würde man auf 3 wachsen, aber dann viermal so lange wachsen. Also $3^4 = e^{\ln(3) \cdot 4} = 81$

Anstatt die Zahlen als solche zu betrachten, kann man sie als etwas betrachten, zu dem e „hinwachsen“ musste. Reelle Zahlen, wie 3, ergeben einen Zinssatz von ln(3) = 1,1, und das ist es, was e „sammelt“, während es weitergeht und kontinuierlich wächst.

Regelmäßiges Wachstum ist einfach: Es „schiebt“ eine Zahl in die gleiche, reale Richtung, in die sie sich bewegt hat. 3 × 3 schiebt eine Zahl in die ursprüngliche Richtung und macht sie dreimal größer (9).

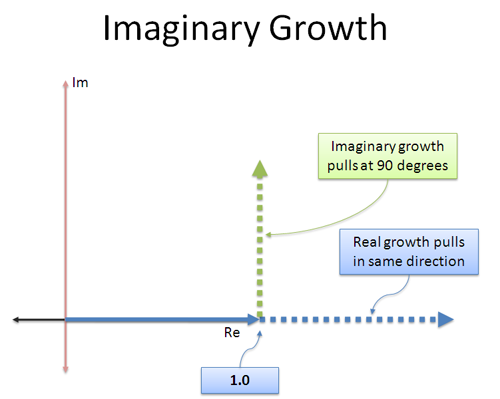
Imaginäres Wachstum ist anders: Die „Zinsen“, die wir verdienen, gehen in eine andere Richtung! Es ist wie ein Düsentriebwerk, das seitlich angeschnallt wurde – anstatt vorwärts zu gehen, beginnen wir im 90-Grad-Winkel zu schieben.

Das Schöne an einem konstanten orthogonalen (senkrechten) Schub ist, dass er uns weder beschleunigt noch verlangsamt – er dreht uns! Nimmt man eine beliebige Zahl und multipliziert sie mit i, so ändert sich nicht ihr Betrag, sondern nur die Richtung, in die sie zeigt.

Intuitiv sehe ich die kontinuierliche imaginäre Wachstumsrate folgendermaßen: „Wenn ich wachse, schiebe mich nicht vor oder zurück in die Richtung, in die ich bereits gehe. Drehe mich stattdessen.“

Aber sollten wir uns nicht immer schneller drehen?

Das habe ich mich auch gefragt. Regelmäßiges Wachstum setzt sich in unserer ursprünglichen Richtung zusammen, also gehen wir 1, 2, 4, 8, 16, multiplizieren jedes Mal 2x und bleiben in den reellen Zahlen. Wir können dies als $e^{\ln(2)x}$ betrachten, was bedeutet, dass wir sofort mit einer Rate von ln(2) für „x“ Sekunden wachsen.

Und hey – wenn unsere Wachstumsrate doppelt so schnell wäre, 2ln(2) gegenüber ln(2), würde es genauso aussehen, als würden wir doppelt so lange wachsen (2x gegenüber x). Die Magie von e lässt uns Rate und Zeit vertauschen; 2 Sekunden mit ln(2) ist das gleiche Wachstum wie 1 Sekunde mit 2ln(2).

Nun stellen wir uns vor, wir haben eine rein imaginäre Wachstumsrate (Ri), die uns dreht, bis wir i erreichen, oder 90 Grad nach oben. Was passiert, wenn wir diese Rate auf 2Ri verdoppeln, werden wir dann den Kreis verlassen?

Nein! Eine Geschwindigkeit von 2Ri bedeutet, dass wir uns doppelt so schnell drehen, oder alternativ, dass wir uns mit einer Geschwindigkeit von R doppelt so lange drehen, aber wir bleiben auf dem Kreis. Doppelt so lange zu rotieren bedeutet, dass wir uns jetzt um 180 Grad drehen.

Wenn wir erst einmal erkannt haben, dass eine exponentielle Wachstumsrate uns von 1 auf i bringen kann, dreht uns eine Erhöhung dieser Rate nur noch mehr. Wir werden dem Kreis nie entkommen.

Wenn unsere Wachstumsrate jedoch komplex ist (a+bi vs. Ri), dann lässt uns der reale Teil (a) ganz normal wachsen, während der imaginäre Teil (bi) uns rotieren lässt. Aber wir wollen uns nicht verzetteln: Bei der Eulerschen Formel, $e^{ix}$, geht es um das rein imaginäre Wachstum, das uns auf dem Kreis hält (mehr dazu später).

Ein schneller Sanity Check

Während des Schreibens musste ich für mich selbst ein paar Fragen klären:

Warum verwenden wir $e^x$, drehen wir nicht die Zahl 1?

e repräsentiert den Prozess, bei 1 zu beginnen und kontinuierlich mit 100% Zinsen für eine Zeiteinheit zu wachsen.

Wenn wir e schreiben, fassen wir diesen gesamten Prozess in einer einzigen Zahl zusammen – e repräsentiert die ganze Tücke des kontinuierlichen Wachstums. In Wirklichkeit bedeutet $e^x$ also: „Beginne bei 1 und wachse kontinuierlich mit 100% für x Sekunden“, und fange bei 1 an, wie wir es wollen.

Aber was macht i als Exponent?

Für einen regulären Exponenten wie $3^4$ fragen wir:

• Was ist die implizite Wachstumsrate? Wir wachsen von 1 auf 3 (die Basis des Exponenten).
• Wie können wir diese Wachstumsrate ändern? Wir skalieren sie um das Vierfache (die Potenz des Exponenten).

Wir können unser Wachstum in das „e“-Format umwandeln: Unsere momentane Rate ist ln(3), und wir erhöhen sie auf ln(3) * 4. Wiederum hat die Potenz des Exponenten (4) unsere Wachstumsrate skaliert.

Wenn der obere Exponent i ist (wie in $3^i$), multiplizieren wir unsere implizite Wachstumsrate einfach mit i. Anstatt mit dem einfachen ln(3) zu wachsen, wachsen wir also mit ln(3) * i.

Der obere Teil des Exponenten modifiziert die implizite Wachstumsrate des unteren Teils.

Die kleinen Details

Sehen wir uns das genauer an. Erinnern Sie sich an diese Definition von e:

Dass $\frac{100\%}{n}$ den Zinsanteil darstellt, den wir in jeder mikroskopischen Periode verdient haben. Wir haben angenommen, dass der Zinssatz in der realen Dimension 100 % beträgt – aber was wäre, wenn er in der imaginären Richtung 100 % betragen würde?

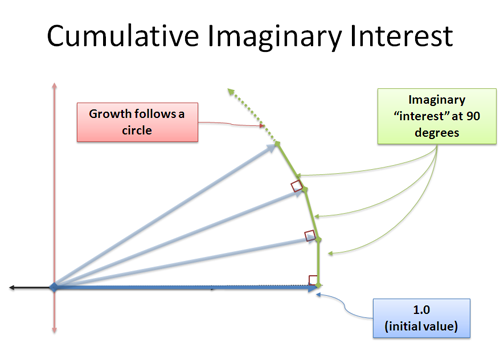
Nun addiert sich unser neu gebildeter Zins in der 90-Grad-Richtung zu uns. Überraschenderweise ändert sich dadurch unsere Länge nicht – das ist ein heikles Konzept, denn es scheint ein Dreieck zu bilden, bei dem die Hypotenuse größer sein muss. Wir haben es hier mit einem Grenzwert zu tun, und der zusätzliche Abstand liegt innerhalb der von uns angegebenen Fehlerspanne. Damit möchte ich mich ein andermal befassen, aber glauben Sie mir: Das kontinuierliche Wachstum der Senkrechten wird Sie drehen. Das ist der Kern von Sinus und Kosinus, bei denen die Veränderung senkrecht zur aktuellen Position erfolgt und man sich im Kreis bewegt.

Wir wenden i Einheiten Wachstum in unendlich kleinen Schritten an, die uns jeweils in einem 90-Grad-Winkel vorwärts bringen. Es gibt keine „immer schnellere“ Drehung – stattdessen kriechen wir entlang des Kreisumfangs eine Strecke von |i| = 1 (Größe von i).

Und hey – die Strecke, die wir um einen Kreis kriechen, ist ein Winkel im Bogenmaß! Wir haben eine weitere Möglichkeit gefunden, eine Kreisbewegung zu beschreiben!

Um eine Kreisbewegung zu erhalten: Kontinuierliche Veränderung durch Rotation im 90-Grad-Winkel (auch bekannt als imaginäre Wachstumsrate).

Die Eulersche Formel besagt also, dass ein exponentielles, imaginäres Wachstum einen Kreis nachzeichnet. Und dieser Weg ist dasselbe wie die Bewegung auf einem Kreis mit Sinus und Kosinus in der imaginären Ebene.

In diesem Fall ist das Wort „exponentiell“ verwirrend, weil wir uns mit einer konstanten Rate um den Kreis bewegen. In den meisten Diskussionen wird davon ausgegangen, dass exponentielles Wachstum einen kumulativen, aufbauenden Effekt hat.

Einige Beispiele

Du glaubst mir nicht wirklich, oder? Hier sind ein paar Beispiele, und wie man sie intuitiv betrachten kann.

Beispiel: $e^i$

Wo ist das x? Ah, es ist nur 1. Intuitiv, ohne den Taschenrechner zu zücken, wissen wir, dass dies „1 Radiant entlang des Einheitskreises“ bedeutet. In meinem Kopf sehe ich, wie „e“ versucht, 1 zu 100 % in dieselbe Richtung zu wachsen, aber „i“ bewegt den Ball und zwingt „1“, entlang des Randes eines Kreises zu wachsen:

Nicht die schönste Zahl, aber so ist es. Denke daran, deinen Rechner in den Bogenmaßmodus zu versetzen, wenn du diese Zahl eingibst.

Beispiel: $3^i$

Das ist knifflig – es ist nicht in unserem Standardformat. Aber denk daran,

Wir wollen ein anfängliches Wachstum von 3x am Ende der Periode, oder eine momentane Rate von ln(3). Aber das i kommt daher und ändert diese Rate von ln(3) in „i * ln(3)“:

Wir dachten, wir würden mit einer regelmäßigen Rate von ln(3) transformieren, etwas schneller als 100% kontinuierliches Wachstum, da e ungefähr 2,718 ist. Aber oh nein, ich habe uns herumgedreht: Jetzt transformieren wir mit einer imaginären Rate, was bedeutet, dass wir uns nur drehen. Wäre i eine regelmäßige Zahl wie 4, wären wir 4x schneller gewachsen. Jetzt wachsen wir mit einer Geschwindigkeit von ln(3), aber seitwärts.

Wir sollten eine komplexe Zahl auf dem Einheitskreis erwarten – es gibt nichts in der Wachstumsrate, das unsere Größe vergrößert. Lösen der Gleichung:

Anstatt also mit „1“ Einheit auf dem Kreis zu enden (wie $e^i$), enden wir mit ln(3) Einheiten.

Beispiel: $i^i$

Vor ein paar Monaten hätte mich das zu Tränen gerührt. Heute nicht mehr! Lasst uns die Umformungen aufschlüsseln:

Wir beginnen mit 1 und wollen sie verändern. Wie lautet die Lösung von $3^i$, was ist die momentane Wachstumsrate, die durch i als Basis dargestellt wird?

Hrm. Normalerweise würden wir ln(x) verwenden, um die Wachstumsrate zu erhalten, die erforderlich ist, um x am Ende einer Zeiteinheit zu erreichen. Aber für eine imaginäre Rate? Da müssen wir etwas herumprobieren.

Um mit 1 zu beginnen und auf i zu wachsen, müssen wir am Anfang mit der Rotation beginnen. Wie schnell? Nun, wir müssen 90 Grad (pi/2 Bogenmaß) in einer Zeiteinheit erreichen. Unsere Rate ist also $i \frac{\pi}{2}$. Denken Sie daran, dass unsere Geschwindigkeit imaginär sein muss, da wir uns drehen und nicht wachsen! Das einfache alte $\frac{\pi}{2}$ ist etwa 1,57 und ergibt ein regelmäßiges Wachstum.

Das sollte Sinn machen: um 1,0 in i am Ende von 1 Einheit zu verwandeln, sollten wir $\frac{\pi}{2}$ Radianten (90 Grad) in dieser Zeitspanne rotieren. Um „i“ zu erhalten, können wir also $e^{i \frac{\pi}{2}}$ verwenden.

Puh. Damit ist i als Basis beschrieben. Wie sieht es mit dem Exponenten aus?

Nun, das andere i sagt uns, dass wir unsere Geschwindigkeit ändern müssen – ja, diese Geschwindigkeit, die wir so lange herausgefunden haben! Anstatt also mit einer Geschwindigkeit von $i \frac{\pi}{2}$ zu rotieren, was eine Basis von i bedeutet, transformieren wir die Rate zu:

Die i’s heben sich auf und machen die Wachstumsrate wieder real! Wir haben unsere Rate gedreht und uns in den negativen Bereich geschoben. Und eine negative Wachstumsrate bedeutet, dass wir schrumpfen – wir sollten erwarten, dass $i^i$ die Dinge kleiner macht. Und das tut sie auch:

Tada! (Suche „i^i“ bei Google, um den Rechner zu benutzen)

Aufatmen: Du kannst intuitiv herausfinden, wie sich imaginäre Basen und imaginäre Exponenten verhalten sollten. Whoa.

Und als Bonus hast du ln(i) herausgefunden – damit $e^x$ zu i wird, musst du e im Bogenmaß $\frac{\pi}{2}$ drehen.

Beispiel: (i^i)^i

Ein doppelter imaginärer Exponent? Wenn du darauf bestehst. Zunächst einmal wissen wir, wie hoch unsere Wachstumsrate innerhalb der Klammer sein wird:

Wir erhalten eine negative (schrumpfende) Wachstumsrate von -pi/2. Und nun modifizieren wir diese Rate wieder um i:

Und nun haben wir eine negative Rotation! Wir bewegen uns mit einer Geschwindigkeit von $-\frac{\pi}{2}$ pro Zeiteinheit um den Kreis. Wie lange gehen wir? Nun, ganz oben in dieser Exponentenkette steht eine implizite Zeiteinheit „1“; die implizite Vorgabe ist 1 Zeiteinheit (genau wie $e = e^1$). 1 Zeiteinheit ergibt eine Drehung von $-\frac{\pi}{2}$ im Bogenmaß (-90 Grad) oder -i!

Und, nur mal so zum Spaß, wenn wir dieses verrückte Ergebnis quadrieren:

Es ist „nur“ die doppelte Drehung: 2 ist eine reguläre Zahl, also verdoppelt sich unsere Drehgeschwindigkeit auf volle -180 Grad in einer Zeiteinheit. Man kann es auch so sehen, dass wir zweimal hintereinander eine Drehung von -90 Grad durchführen.

Auf den ersten Blick sind das wirklich seltsame Exponenten. Aber mit unseren Analogien können wir sie in den Griff bekommen.

Komplexes Wachstum

Wir können reales und imaginäres Wachstum gleichzeitig haben: der reale Teil vergrößert uns, und der imaginäre Teil dreht uns herum:

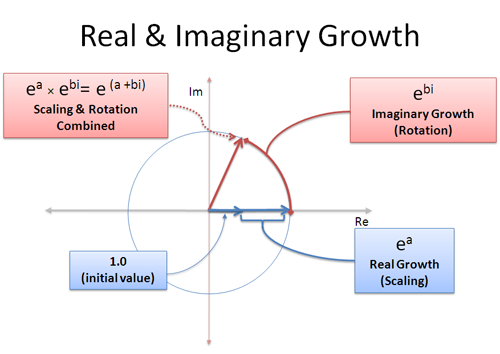
Eine komplexe Wachstumsrate wie (a + bi) ist eine Mischung aus realem und imaginärem Wachstum. Der reale Teil a bedeutet „Wachstum mit 100% für a Sekunden“ und der imaginäre Teil b bedeutet „Rotation für b Sekunden“. Vergiss nicht, dass Rotationen nicht den Vorteil der Aufsummierung haben, da du immer wieder in eine andere Richtung „schiebst“ – Rotation addiert sich linear.

Mit diesem Wissen können wir jeden Punkt auf einem beliebig großen Kreis mit (a+bi) darstellen! Der Radius ist $e^a$ und der Winkel wird durch $e^{bi}$ bestimmt. Das ist so, als würde man die Zahl zweimal in das Expansions-O-Tron stecken: einmal, um sie auf die richtige Größe zu bringen (a Sekunden), ein zweites Mal, um sie auf den richtigen Winkel zu drehen (b Sekunden). Oder man könnte sie erst drehen und dann wachsen lassen!

Angenommen, wir wollen den Wachstumsbetrag wissen, um auf 6 + 8i zu kommen. Das ist eigentlich eine Frage nach dem natürlichen Logarithmus einer imaginären Zahl: Wie wächst e, um (6 + 8i) zu erhalten?

• Radius: Wie groß ist der Kreis, den wir brauchen? Nun, die Größenordnung ist $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Das bedeutet, dass wir für ln(10) = 2,3 Sekunden wachsen müssen, um diesen Betrag zu erreichen.
• Betrag zum Drehen: Wie groß ist der Winkel zu diesem Punkt? Wir können arctan verwenden, um es herauszufinden: atan(8/6) = 53 Grad = .93 Radiant.
• Kombiniere das Ergebnis: ln(6+8i) = 2.3 + .93i

Das heißt, wir können den Zufallspunkt (6 + 8i) erreichen, wenn wir $e^{2.3 + .93i}$.

Warum ist das nützlich?

Die Eulersche Formel gibt uns eine weitere Möglichkeit, die Bewegung auf einem Kreis zu beschreiben. Aber das können wir auch schon mit Sinus und Kosinus – was ist daran so besonders?

Es geht um die Perspektive. Sinus und Kosinus beschreiben die Bewegung in Form eines Gitters, indem sie horizontale und vertikale Koordinaten aufzeichnen.

Die Eulersche Formel verwendet Polarkoordinaten – wie groß sind dein Winkel und dein Abstand? Auch hier gibt es zwei Möglichkeiten, Bewegung zu beschreiben:

• Gittersystem: Gehe 3 Einheiten nach Osten und 4 Einheiten nach Norden
• Polarkoordinaten: Gehe 5 Einheiten in einem Winkel von 53,13 Grad

Abhängig von der Problemstellung sind polare oder rechtwinklige Koordinaten nützlicher. Mit der Eulerschen Formel können wir zwischen beiden umrechnen, um das beste Werkzeug für die Aufgabe zu verwenden. Da $e^{ix}$ in Sinus und Kosinus umgewandelt werden kann, können wir auch Formeln in Trigonometrie als Variationen von e umschreiben, was sehr praktisch ist (man muss sich sin(a+b) nicht merken, man kann es ableiten – mehr dazu ein anderes Mal). Und es ist schön, dass jede Zahl, ob real oder komplex, eine Variation von e ist.

Aber Nutzen, Nutzen, Nutzen: Das wichtigste Ergebnis ist die Erkenntnis, dass verwirrende Gleichungen mit den richtigen Analogien intuitiv werden können. Lassen Sie nicht zu, dass schöne Gleichungen wie die Eulersche Formel ein Zauberspruch bleiben – bauen Sie auf den Analogien auf, die Sie kennen, um die Einsichten in der Gleichung zu erkennen.

Happy math.

Anhang

Der Screencast hat Spaß gemacht, und Feedback ist definitiv willkommen. Ich denke, es hilft den Ideen aufzufallen, und den Artikel durchzugehen hat mir geholfen, Lücken in meiner Intuition zu finden.

• Brian Slesinsky hat eine tolle Präsentation über die Eulersche Formel
• Visual Complex Analysis hat eine großartige Diskussion über die Eulersche Formel – siehe S. 10 in der Google Buchvorschau
• Ich habe einen Vortrag über Mathematik und Analogien gehalten, der die Eulersche Identität visueller erklärt:

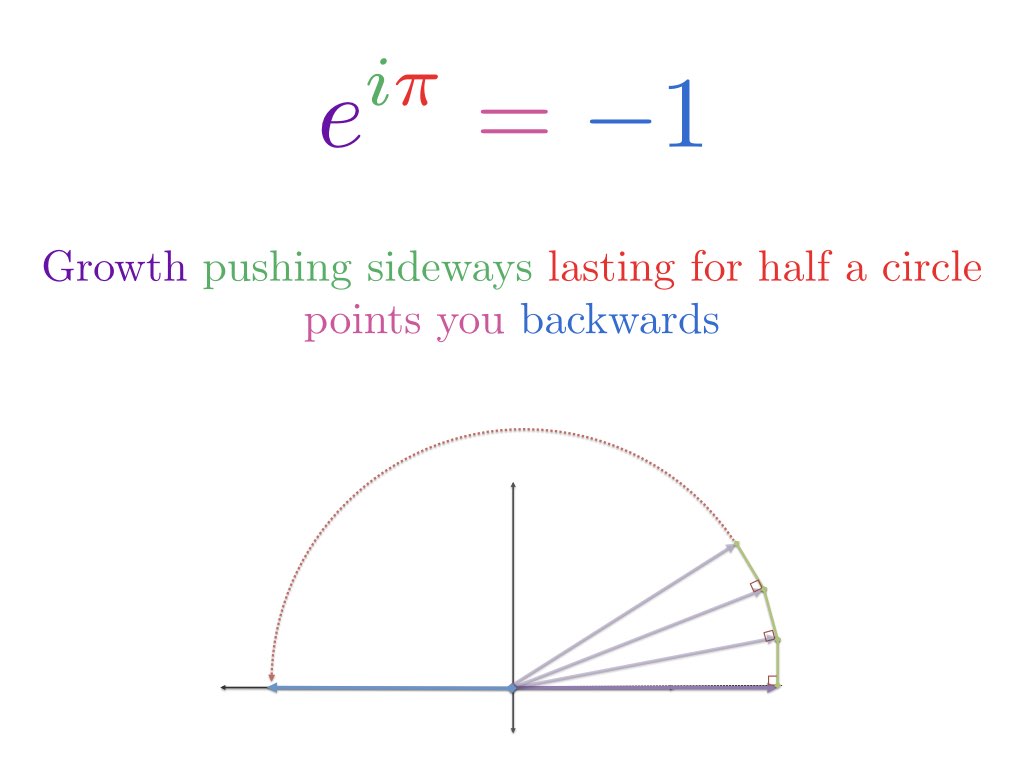
Weitere Beiträge in dieser Reihe

1. Ein visueller, intuitiver Leitfaden für imaginäre Zahlen
2. Intuitives Rechnen mit komplexen Zahlen
3. Verstehen, warum komplexe Multiplikation funktioniert
4. Intuitiver Leitfaden für Winkel, Grad und Bogenmaß
5. Intuitives Verständnis der Eulerschen Formel
6. Ein interaktiver Leitfaden zur Fourier-Transformation
7. Intuitiver Leitfaden zur Faltung
8. Intuitives Verständnis von Sinuswellen
9. Ein intuitiver Leitfaden für die Lineare Algebra
10. Eine Programmierer-Intuition für die Matrix-Multiplikation
11. Imaginäre Multiplikation vs. Imaginäre Exponenten