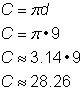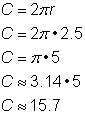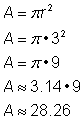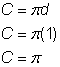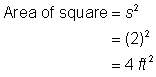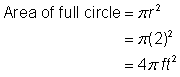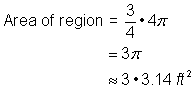Kreise
Lernziel(e)
– Eigenschaften von Kreisen erkennen.
– Den Umfang eines Kreises bestimmen.
– Den Flächeninhalt eines Kreises bestimmen.
– Den Flächeninhalt und den Umfang von zusammengesetzten geometrischen Figuren bestimmen.
Einführung
Kreise sind eine häufige Form. Man sieht sie überall – die Räder eines Autos, Frisbees, die durch die Luft fliegen, Compact Discs, die Daten übertragen. All das sind Kreise.
Ein Kreis ist eine zweidimensionale Figur, genau wie Polygone und Vierecke. Allerdings werden Kreise anders gemessen als diese anderen Formen – man muss sogar einige andere Begriffe verwenden, um sie zu beschreiben. Werfen wir einen Blick auf diese interessante Form.
Eigenschaften von Kreisen
Ein Kreis stellt eine Reihe von Punkten dar, die alle den gleichen Abstand zu einem festen Mittelpunkt haben. Dieser feste Punkt wird als Mittelpunkt bezeichnet. Der Abstand vom Mittelpunkt des Kreises zu einem beliebigen Punkt auf dem Kreis wird Radius genannt.
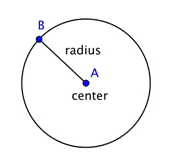
Wenn zwei Radien (Plural von Radius) zu einem Liniensegment durch den Kreis zusammengefügt werden, erhält man einen Durchmesser. Der Durchmesser eines Kreises geht durch den Mittelpunkt des Kreises und hat seine Endpunkte auf dem Kreis selbst.
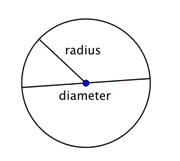
Der Durchmesser eines beliebigen Kreises ist das Zweifache der Länge des Radius dieses Kreises. Er kann durch den Ausdruck 2r dargestellt werden, oder „das Zweifache des Radius“. Wenn du also den Radius eines Kreises kennst, kannst du ihn mit 2 multiplizieren, um den Durchmesser zu finden; das bedeutet auch, dass du, wenn du den Durchmesser eines Kreises kennst, durch 2 dividieren kannst, um den Radius zu finden.
|
Beispiel |
||
|
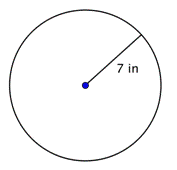
Problem |
Finde den Durchmesser des Kreises.
|
|
|
d = 2r d = 2(7) d = 14 |
Der Durchmesser ist das Zweifache des Radius, also 2r. Der Radius dieses Kreises ist 7 Zoll, also ist der Durchmesser 2(7) = 14 Zoll. |
|
|
Antwort |
Der Durchmesser ist 14 Zoll. |
|
|
Beispiel |
||
|
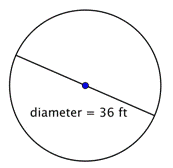
Problem |
Bestimme den Radius des Kreises.
|
|
|
|
Der Radius ist die Hälfte des Durchmessers, also |
|
|
Antwort |
Der Radius ist 18 Fuß. |
|
Umfang
Den Abstand um einen Kreis nennt man den Umfang. (Zur Erinnerung: Der Abstand um ein Polygon ist der Umfang.)
Eine interessante Eigenschaft von Kreisen ist, dass das Verhältnis von Kreisumfang und Durchmesser für alle Kreise gleich ist. Unabhängig von der Größe des Kreises ist das Verhältnis von Umfang und Durchmesser dasselbe.
Nachfolgend sind einige tatsächliche Messungen verschiedener Gegenstände angegeben. Die Messungen sind auf den nächsten Millimeter oder Viertelzoll genau (je nach der verwendeten Maßeinheit). Schauen Sie sich das Verhältnis zwischen Umfang und Durchmesser für jeden Gegenstand an – obwohl die Gegenstände unterschiedlich sind, ist das Verhältnis für jeden Gegenstand ungefähr gleich.
|
Einzelteil |
Umfang (C) (gerundet auf das nächste Hundertstel) |
Durchmesser (d) |
Verhältnis |
|
Cup |
253 mm |
79 mm |
|
|
Viertel |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
Der Umfang und der Durchmesser sind ungefähre Maße, da es keine genaue Möglichkeit gibt, diese Maße exakt zu messen. Könnte man sie jedoch genauer messen, würde man feststellen, dass sich das Verhältnis ![]() für jeden der angegebenen Punkte auf 3,14 zubewegt. Der mathematische Name für das Verhältnis
für jeden der angegebenen Punkte auf 3,14 zubewegt. Der mathematische Name für das Verhältnis ![]() ist pi und wird durch den griechischen Buchstaben
ist pi und wird durch den griechischen Buchstaben ![]() dargestellt.
dargestellt.
![]() ist eine nicht abschließende, sich nicht wiederholende Dezimalzahl, so dass es unmöglich ist, sie vollständig auszuschreiben. Die ersten 10 Ziffern von
ist eine nicht abschließende, sich nicht wiederholende Dezimalzahl, so dass es unmöglich ist, sie vollständig auszuschreiben. Die ersten 10 Ziffern von ![]() sind 3,141592653; sie werden oft auf 3,14 gerundet oder als Bruch
sind 3,141592653; sie werden oft auf 3,14 gerundet oder als Bruch ![]() geschätzt. Beachte, dass sowohl 3,14 als auch
geschätzt. Beachte, dass sowohl 3,14 als auch ![]() Näherungswerte von
Näherungswerte von![]() sind und in Berechnungen verwendet werden, bei denen es nicht wichtig ist, genau zu sein.
sind und in Berechnungen verwendet werden, bei denen es nicht wichtig ist, genau zu sein.
Da du weißt, dass das Verhältnis von Umfang zu Durchmesser (oder ![]() ) für alle Kreise gleich ist, kannst du diese Zahl verwenden, um den Umfang eines Kreises zu bestimmen, wenn du seinen Durchmesser kennst.
) für alle Kreise gleich ist, kannst du diese Zahl verwenden, um den Umfang eines Kreises zu bestimmen, wenn du seinen Durchmesser kennst.
![]() =
= ![]() , also C =
, also C = ![]() d
d
Auch, da d = 2r, dann C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Umfang eines Kreises
Um den Umfang (C) eines Kreises zu ermitteln, verwendet man eine der folgenden Formeln:
Wenn man den Durchmesser (d) eines Kreises kennt: ![]()
Wenn du den Radius (r) eines Kreises kennst: ![]()
|
Beispiel |
||
|
Problem |
Bestimme den Umfang des Kreises.
|
|
|
|
Um den Umfang bei einem Durchmesser von 9 Zoll zu berechnen, verwende die Formel Da du einen Näherungswert für |
|
|
Antwort |
Der Umfang beträgt 9 |
|
|
Beispiel |
||
|
Problem |
Bestimme den Umfang eines Kreises mit einem Radius von 2.5 m. |
|
|
|
Um den Umfang eines Kreises mit einem Radius von 2,5 m zu berechnen, benutze die Formel |
|
|
Antwort |
Der Umfang beträgt 5 |
|
Ein Kreis hat einen Radius von 8 Zoll. Wie groß ist sein Umfang, aufgerundet auf den nächsten Zoll?
A) 25 Zoll
B) 50 Zoll
C) 64 Zoll2
D) 201 Zoll
Die Fläche
![]() ist eine wichtige Zahl in der Geometrie. Du hast sie schon benutzt, um den Umfang eines Kreises zu berechnen. Du verwendest
ist eine wichtige Zahl in der Geometrie. Du hast sie schon benutzt, um den Umfang eines Kreises zu berechnen. Du verwendest ![]() auch, wenn du den Flächeninhalt eines Kreises berechnest.
auch, wenn du den Flächeninhalt eines Kreises berechnest.
Flächeninhalt eines Kreises
Um den Flächeninhalt (A) eines Kreises zu bestimmen, verwendest du die Formel: ![]()
|
Beispiel |
||
|
Problem |
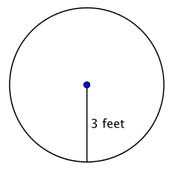
Bestimme den Flächeninhalt des Kreises.
|
|
|
|
Bestimme den Flächeninhalt dieses Kreises mit der Formel Denken Sie daran, die Antwort in Quadrateinheiten zu schreiben, da Sie den Flächeninhalt finden. |
|
|
Antwort |
Der Flächeninhalt ist 9 |
|
Ein Knopf hat einen Durchmesser von 20 Millimetern. Wie groß ist die Fläche des Knopfes? Verwenden Sie 3,14 als Näherungswert ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Zusammengesetzte Figuren
Nachdem du nun weißt, wie man den Umfang und die Fläche eines Kreises berechnet, kannst du dieses Wissen nutzen, um den Umfang und die Fläche von zusammengesetzten Figuren zu bestimmen. Der Trick, um diese Art von Problemen zu lösen, besteht darin, Formen (und Teile von Formen) innerhalb der zusammengesetzten Figur zu identifizieren, ihre einzelnen Dimensionen zu berechnen und sie dann zu addieren.
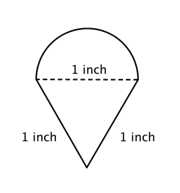
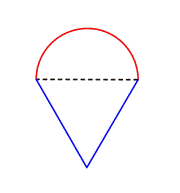
Betrachten Sie zum Beispiel das folgende Bild. Ist es möglich, den Umfang zu bestimmen?
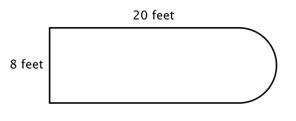
Der erste Schritt besteht darin, einfachere Figuren innerhalb dieser zusammengesetzten Figur zu identifizieren. Du kannst sie in ein Rechteck und einen Halbkreis zerlegen, wie unten gezeigt.
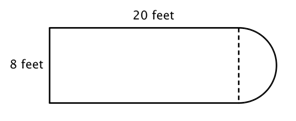
Du weißt, wie man den Umfang eines Rechtecks findet, und du weißt, wie man den Umfang eines Kreises findet. Hier ist der Umfang der drei festen Seiten des Rechtecks 8 + 20 + 20 = 48 Fuß. (Beachte, dass nur drei Seiten des Rechtecks in den Umfang der zusammengesetzten Figur eingehen, weil die andere Seite nicht an einer Kante liegt; sie wird vom Halbkreis bedeckt!)
Um den Umfang des Halbkreises zu finden, benutze die Formel ![]() mit einem Durchmesser von 8 Fuß und nimm dann die Hälfte des Ergebnisses. Der Umfang des Halbkreises ist
mit einem Durchmesser von 8 Fuß und nimm dann die Hälfte des Ergebnisses. Der Umfang des Halbkreises ist ![]() oder ungefähr 12,56 Fuß, also ist der Gesamtumfang ungefähr 60,56 Fuß.
oder ungefähr 12,56 Fuß, also ist der Gesamtumfang ungefähr 60,56 Fuß.
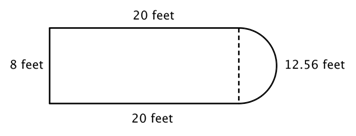
|
Beispiel |
||
|
Problem |
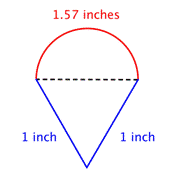
Bestimme den Umfang (auf ein Hundertstel genau) der zusammengesetzten Figur, die aus einem Halbkreis und einem Dreieck besteht.
|
|
|
|
Erkenne kleinere Formen innerhalb der zusammengesetzten Figur. Diese Figur enthält einen Halbkreis und ein Dreieck. |
|
|
Durchmesser (d) = 1
Umfang des Halbkreises = |
Bestimme den Umfang des Kreises. Dividiere dann durch 2, um den Umfang des Halbkreises zu ermitteln. |
|
|
|
|
Ermittle den Gesamtumfang, indem du den Umfang des Halbkreises und die Längen der beiden Schenkel addierst. Da wir den Umfang des Halbkreises nur annähernd messen, ist auch der Umfang ein Näherungswert. |
|
Antwort |
Rund 3.57 Zoll |
|
|
Beispiel |
||
|
Problem |
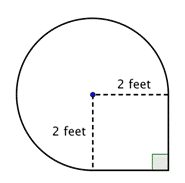
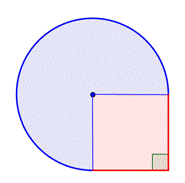
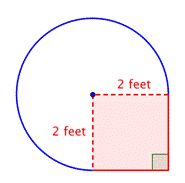
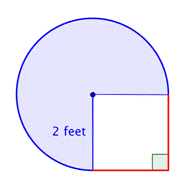
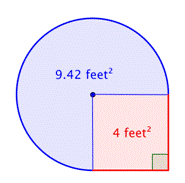
Ermitteln Sie die Fläche der zusammengesetzten Figur, die aus drei Vierteln eines Kreises und einem Quadrat besteht, auf ein Hundertstel genau.
|
|
|
|
Erkenne kleinere Formen innerhalb der zusammengesetzten Figur. Diese Figur enthält einen kreisförmigen Bereich und ein Quadrat. Wenn man den Flächeninhalt der beiden findet, kann man den Flächeninhalt der gesamten Figur bestimmen. |
|
|
|
Bestimme den Flächeninhalt des Quadrats. |
|
|
|
|
Bestimme die Fläche des kreisförmigen Bereichs. Der Radius beträgt 2 Fuß. Beachte, dass der Bereich |
|
|
4 Fuß2 + |
Addiere die beiden Bereiche zusammen. Da du die Fläche des Kreises nur annähernd gemessen hast, ist auch die Fläche der Figur ein Näherungswert. |
|
Antwort |
Die Fläche beträgt ungefähr 13.42 Fuß2. |
|
Wie groß ist die Fläche (auf ein Hundertstel genau) der unten abgebildeten Figur? (Beide gerundeten Bereiche sind Halbkreise.)
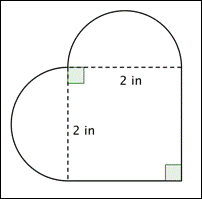
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3.14 in2
Zusammenfassung
Kreise sind eine wichtige geometrische Form. Der Abstand um einen Kreis wird als Umfang bezeichnet, und der Innenraum eines Kreises wird als Fläche bezeichnet. Um den Umfang und die Fläche eines Kreises zu berechnen, benötigt man eine Zahl namens Pi (![]() ), die eine nicht endende, sich nicht wiederholende Dezimalzahl ist. Pi wird oft durch die Werte 3,14 und
), die eine nicht endende, sich nicht wiederholende Dezimalzahl ist. Pi wird oft durch die Werte 3,14 und ![]() angenähert. Sie können den Umfang oder die Fläche zusammengesetzter Formen – einschließlich Formen, die kreisförmige Abschnitte enthalten – ermitteln, indem Sie die Formeln für den Umfang und die Fläche anwenden, wo es angebracht ist.
angenähert. Sie können den Umfang oder die Fläche zusammengesetzter Formen – einschließlich Formen, die kreisförmige Abschnitte enthalten – ermitteln, indem Sie die Formeln für den Umfang und die Fläche anwenden, wo es angebracht ist.