
Galileo wird oft als der Vater der modernen Wissenschaft angesehen. Er war derjenige, der die Prinzipien des Experiments, der Theorie und der Mathematik zu einem einheitlichen Rahmen zusammenfügte. Wahrscheinlich war Galilei mehr als jeder andere für die Entwicklung der modernen Wissenschaft verantwortlich.
Es heißt, dass Galilei zwei Stahlkugeln unterschiedlicher Masse, aber aus demselben Material, vom schiefen Turm von Pisa fallen ließ und sie gleichzeitig landeten. Bemerkenswert an diesem Experiment ist, dass er eine neue Methode der Wissenschaft einführte, bei der man ein Experiment durchführt, um eine Hypothese zu testen. Er zeigte, dass wir mehr tun müssen, als nur zu glauben, dass etwas wahr ist, sondern dass wir es auch beweisen müssen.

Galileo fand ein interessantes Paradoxon, als er Leiter der mathematischen Fakultät der Universität von Pisa war.
Definition: Ein Paradoxon, auch Antinomie genannt, ist eine logisch in sich widersprüchliche Aussage oder eine Aussage, die der eigenen Erwartung zuwiderläuft. (Wikipedia). (Griechisch: „para“ = jenseits, „doxa“ = Glaube)
Bei Galileis Paradoxon ging es darum, festzustellen, ob zwei Mengen mit unendlichen Objekten einander gleichwertig sind. Zum Beispiel sei P die Menge der positiven ganzen Zahlen mit P= {0,1,2,3,…} und E die Menge der geraden Zahlen mit E = {0,2,4,6,…}. Galilei behauptete, dass die Größe dieser beiden Mengen gleich sein wird, weil wir jede positive ganze Zahl aus der Menge P mit den geraden Zahlen aus der Menge E paaren können.

Wie kann also die Größe der beiden Mengen gleich sein, wenn eine „weniger“ Zahl in E erscheint? Dies wurde das Galilei-Paradoxon genannt und löste eine neue Debatte über das Konzept der Unendlichkeit aus.
Nach Galilei wurde sein Schüler Evangelista Torricelli Leiter der Abteilung für Mathematik an der Universität Pisa. Sie kennen ihn vielleicht wegen seiner Arbeiten über den atmosphärischen Druck und die Erfindung des Barometers. Da Toricelli sich auch für Mathematik interessiert, fragt er:
Ist es möglich, ein Objekt mit einem endlichen Volumen und einer unendlichen Oberfläche zu haben? Zunächst scheint so etwas für die meisten von uns unwahrscheinlich zu sein. Aber die Mathematik sagt uns, dass so etwas möglich ist. Torricelli beantwortete seine Frage selbst und entdeckte die Toricelli-Trompete, deren Oberfläche unendlich ist, deren Volumen jedoch endlich ist. Seine Entdeckung wird als „unglaubliches“ Paradoxon angesehen.
Es gibt übrigens eine wesentliche Regel in der Philosophie der Mathematik: Mit welcher Epoche der Philosophie oder Mathematik man sich auch immer beschäftigt, sie steht in Zusammenhang mit der Geschichte, Kultur und Religion dieser Region. Deshalb nennt man Toricellis Trompete auch Gabriels Horn. Hier wird ein Bezug zur Bibel hergestellt, weil die Christen glauben, dass der Engel Gabriel das Horn am Tag des Jüngsten Gerichts blasen wird.
Wie entsteht also Toricellis Trompete? Wir alle wissen, wie man y=x graphisch darstellt. Wenn man stattdessen die Gleichung y=1/x graphisch darstellt, wobei x größer oder gleich 1 ist, sieht der Graph wie folgt aus:
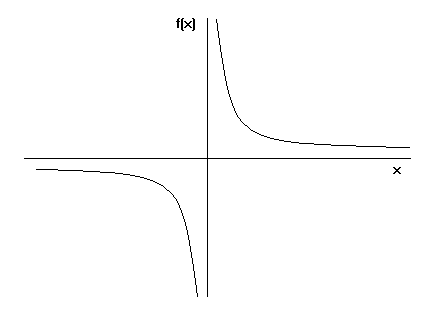
Wenn wir den Graphen von y=1/x nehmen und ihn um die x-Achse drehen, sehen wir die Toricelli-Trompete.

Glücklicherweise haben wir mathematische Formeln in der Hand, um die Fläche und das Volumen der Toricelli-Trompete zu berechnen. Wenn wir die untenstehende Integrationsformel für das Volumen der Trompete verwenden, erhalten wir einen endlichen Betrag.
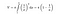
Wenn wir jedoch die Integrationsformel für die Oberfläche der Trompete anwenden, wird die Oberfläche dieses Mal unendlich groß. Ist dieses Ergebnis nicht interessant?
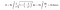
Da das Volumen von Toricellis Trompete endlich ist, können wir sie mit einer endlichen Menge an Farbe füllen. Nehmen wir zum Beispiel an, dass das Volumen der Trompete 100 Liter beträgt. Ich gehe zum Baumarkt, kaufe 100 Liter Farbe und fülle sie ein. Das Interessante daran ist jedoch, dass ich mit diesen 100 Litern Farbe eine unendliche Fläche gestrichen habe. Heute nennen die meisten Leute dieses Paradoxon „das Malerparadoxon“
Houston, wir haben hier ein Problem! Die Situation, die in der Praxis unmöglich ist, wird in der Mathematik möglich. Wie kann also Torricellis Trompete real sein? Oder wie können wir alle Elemente der Mengen genau zuordnen, wenn in Galileis Beispiel eine der Mengen eine Teilmenge einer anderen ist?
Der Grund für all diese Konflikte ist, dass das Konzept der Unendlichkeit nicht mit anderen Konzepten, die wir kennen, vergleichbar ist, und das verwirrt viele Menschen. Galilei sagt zu seinem Paradoxon,
„Ja, mein Freund, es gibt die Unendlichkeit. Es ist zwecklos, sich dagegen zu wehren. Die Mengen, an denen ich arbeite, sind Beispiele für geschlossene Mengen, die Unendlichkeit beinhalten. Sie beginnen an einem Punkt und gehen bis ins Unendliche, und doch sind sie immer noch Mengen. Meine Kommentare und Konzepte zur Unendlichkeit müssen sich jedoch von denen unterscheiden, die ich für endliche Größen verwenden würde. Wenn man es mit endlichen Größen zu tun hat, kann man sagen, dass 3 Kilo weniger sind als 5 Kilo, oder dass 32 Meter länger sind als 7 Meter. Aber wenn es um die Unendlichkeit geht, kann man nicht sagen, dass diese Unendlichkeit größer, kleiner oder gleich der anderen ist.“
Das war Galileis Lösung im Jahre 1600.
Unglücklicherweise hatte Galileis Lösung eine neue Debatte über die Unendlichkeit ausgelöst. Mathematiker und Philosophen konnten sich nicht auf eine konkrete Antwort einigen, bis Cantor seine „Mengenlehre“ vorstellte, die Schüler heute in der Grundschule lernen.
Wir können die Entwicklung der Idee der Unendlichkeit periodisch historisieren. Sie entstand zuerst bei den Eleaten, einer vorsokratischen Philosophenschule, die von Parmenides im frühen fünften Jahrhundert v. Chr. in der antiken Stadt Elea gegründet wurde. Dieser Schule gehörten drei große Philosophen an, darunter Zenon, Xenophanes und Parmenides. In dieser Schule war die akzeptierte Philosophie, dass die Existenz singulär ist und es keine Pluralität gibt. Zenon war berühmt für seine Paradoxa über die Unendlichkeit bei den Eleaten. Später in den 300er Jahren v. Chr., Aristoteles kam auf und schlug ein Begriffspaar vor, um Zenos Paradoxe zu erklären, nämlich die potentielle Unendlichkeit und die tatsächliche Unendlichkeit.
Die potentielle Unendlichkeit ist eine Gruppe von Zahlen oder eine Gruppe von „Dingen“, die sich fortsetzt, ohne zu enden, die weitergeht oder sich immer wieder wiederholt, ohne dass ein Endpunkt erkennbar ist.
Das tatsächliche Unendliche umfasst nie endende Mengen oder „Dinge“ innerhalb eines Raumes, der einen Anfang und ein Ende hat; es ist eine Reihe, die technisch „abgeschlossen“ ist, aber aus einer unendlichen Anzahl von Gliedern besteht.
Aristoteles glaubte, dass es keine tatsächliche Unendlichkeit gibt. Diese Idee von Aristoteles beherrschte die Welt der Philosophie bis zum 16. Jahrhundert. Dann behaupteten Philosophen wie Cusa und Bruno, dass es eine tatsächliche Unendlichkeit gibt, aber wir können sie nicht verstehen. Nach Cuso und Bruno befasste sich der große Denker Spinoza mit dem Thema.
Spinoza sagte, dass wir das Konzept der Unendlichkeit verstehen und sie nach Größe ordnen könnten. Er sagte aber auch, dass er sie nicht berechnen könne. Er konnte zum Beispiel 3 zu 5 addieren, aber er konnte nicht eine Unendlichkeit zu einer anderen addieren.
Um diese Debatten zu beenden, tauchte schließlich ein schöner Mann auf, Georg Cantor, und begründete die Mengenlehre, die immer noch die Grundlage der Mathematik ist. Er setzte mit seiner Mengenlehre den Schlusspunkt in der Unendlichkeitsdiskussion.
Er zeigte uns, dass eine unendliche Menge größer oder kleiner als eine andere unendliche Menge ist. Außerdem behauptete Cantor, dass wir unendliche Mengen addieren und multiplizieren können. Bis dahin hatten sich die Menschen an Aristoteles‘ Vorstellungen von der Unendlichkeit orientiert. Nach Aristoteles wäre die Zahl 3, wenn man sie mit der Unendlichkeit multipliziert, wieder unendlich. Die Unendlichkeit würde alles verschlingen. Auf dieser Grundlage behauptete er, dass es nur eine potenzielle Unendlichkeit und keine tatsächliche Unendlichkeit gäbe.
Cantor bewies uns jedoch mit der Mengenlehre das Gegenteil von Aristoteles‘ Idee. Wenn wir zu einer unendlichen Menge eins hinzufügen, ist es nicht mehr dieselbe Menge. Er versuchte, die Unendlichkeiten zu vergleichen. Cantor bewies zum Beispiel, dass die Menge aller Funktionen von (0,1)→ℕ abzählbar ist. So definierte er eine Eins-zu-Eins- und Onto-Funktion vom Intervall (0,1) zu den natürlichen Zahlen.
Mit anderen Worten, er bewies, dass alle natürlichen Zahlen zwischen 0 und 1 passen, weil es unendlich viele rationale Zahlen zwischen 0-1 gibt, und diese Unendlichkeiten können miteinander verglichen werden. Dann tat er etwas noch Gefährlicheres, als zwei gleiche Unendlichkeiten zu finden. Er verglich die Unendlichkeit der reellen Zahlen mit der Unendlichkeit der natürlichen Zahlen und stellte fest, dass die Unendlichkeit der reellen Zahlen größer ist als die andere. Er sah sich sogar seinen Beweis an und sagte zu seinem Freund Dedekind: „Ich sehe es, aber selbst ich kann es nicht glauben …“.
Cantor war auch ein Mathematiker mit sehr ernsten philosophischen und religiösen Bedenken. Als er die Mengenlehre entwickelte, sagte er: „Gott hat mir die Mengenlehre diktiert“.
Die Mengenlehre war nicht weithin akzeptiert, als sie zum ersten Mal entwickelt wurde. Unternehmen stellten Cantor nicht einmal für eine Stelle ein. Ein Mathematiker, Henri Poincaré, sagte einmal: „Die Ideen dieses Cantor sind eine schlimme Krankheit, die der Mathematik an den Kragen geht. Und die Mathematik wird ihn eines Tages behandeln“. Cantor musste eine Zeit lang in eine Nervenheilanstalt gehen und starb dort. Aber heute halten wir ihn für ein Genie.
Cantor war ein einsamer Mann am Rande der Unendlichkeit. Er zitierte zu Beginn seines Artikels über transfinite Zahlen die Bibel: „Alles, was verborgen ist, wird ans Licht gebracht werden.“