Im Tipp des Monats November 2011 (TOTM) haben wir die Kompressorberechnungen einer Fallstudie vorgestellt. Wir verglichen die Ergebnisse der rigorosen Methode mit den Werten der Abkürzungsmethoden. Die strenge Methode basierte auf einer Zustandsgleichung wie der Soave-Redlich-Kwong (SRK) zur Berechnung der erforderlichen Enthalpien und Entropien. Die Enthalpien und Entropien werden zur Bestimmung des Leistungsbedarfs und der Entladetemperaturen verwendet. Die Ergebnisse deuten darauf hin, dass die Genauigkeit der Shortcut-Methode empfindlich auf den Wert des Verhältnisses der Wärmekapazität im idealen Gaszustand, k, reagiert.
Alleine aus rechnerischer Sicht ist die Leistungsberechnung besonders empfindlich auf die Angabe des Massendurchsatzes, der Ansaugtemperatur und des Ansaugdrucks sowie der Ausblastemperatur und des Auslassdrucks. Ein Kompressor wird unter verschiedenen Werten der Variablen, die seine Leistung beeinflussen, arbeiten. Daher ist der schwierigste Teil einer Kompressorberechnung die Festlegung eines angemessenen Bereichs für jede Variable und nicht die Berechnung selbst. Die Referenz betont, dass die Verwendung eines einzigen Wertes für jede Variable nicht der richtige Weg ist, um ein Kompressionssystem zu bewerten.
Normalerweise werden die thermodynamischen Berechnungen für einen idealen (reversiblen) Prozess durchgeführt. Die Ergebnisse eines reversiblen Prozesses werden dann durch die Verwendung eines thermodynamischen Wirkungsgrades an die reale Welt angepasst. Beim Kompressionsprozess gibt es drei ideale Prozesse, die dargestellt werden können: 1) ein isothermer Prozess (PV1=C1), 2) ein isentroper Prozess (PVk=C2) und 3) ein polytroper Prozess (PVn=C3). Jedes dieser Verfahren kann in geeigneter Weise als Grundlage für die Bewertung des Kompressionsleistungsbedarfs durch manuelle oder rechnerische Berechnung verwendet werden. Der isotherme Prozess wird jedoch nur selten als Grundlage verwendet, da der normale industrielle Verdichtungsprozess nicht einmal annähernd bei konstanter Temperatur durchgeführt wird.
Beachten Sie, dass Dresser Rand ziemlich viel Arbeit mit der „Nahezu konstanten Temperatur“-Kompression leistet, insbesondere für die CO2-Verdichtung aus Abluftkaminen. Für Details siehe:
In diesem TOTM wird demonstriert, wie man den Wirkungsgrad eines Kompressors aus gemessenem Durchfluss, Zusammensetzung, Ansaug- und Ausblastemperaturen und -drücken bestimmen kann. Eine strenge, auf einer Zustandsgleichung basierende Berechnung und eine Abkürzungsmethode werden betrachtet und die Ergebnisse verglichen.
Kompressoreffizienz
Kompressoreffizienzen variieren je nach Kompressortyp, Größe und Durchsatz. Sie können (nachträglich) nur durch einen Kompressortest ermittelt werden, obwohl die Kompressorhersteller in der Regel gute Schätzungen abgeben können. Für Planungszwecke werden die folgenden Werte für die Gesamtwirkungsgrade vorgeschlagen:
Tabelle 1. Gesamtwirkungsgrade von Verdichtern
|
Kompressortyp |
Wirkungsgrad, η |
|
Zentrifugal |
0.70 – 0.85 |
|
Hochgeschwindigkeits-Hubkolbenmaschinen |
0.72 – 0.85 |
|
Niedergeschwindigkeits-Hubkolbenmaschinen |
0.75 – 0,90 |
|
Schraubenverdichter |
0,65 – 0,75 |
Diese Gesamtefffizienzen umfassen die Gasreibung innerhalb des Verdichters, die mechanischen Verluste (Lager, Dichtungen, Getriebe usw.) und die Verluste des Getriebes. Der mechanische Wirkungsgrad hängt von der Größe und dem Typ des Verdichters ab, aber 95 % ist eine nützliche Planungszahl. Bei der Berechnung der Verdichterförderhöhe und der Austrittstemperatur wird die isentrope oder polytrope Effizienz verwendet (die isentrope Effizienz wird manchmal auch als adiabatische Effizienz bezeichnet). Addiert man zu den Gesamteffizienzen in Tabelle 1 3-4 % Effizienzen (mechanische Verluste), so erhält man im Allgemeinen eine gute Schätzung der thermodynamischen Effizienzen.
Zur Bewertung der Leistung eines vorhandenen Verdichters besteht das Ziel darin, den Verdichterwirkungsgrad (η) und den Leistungsbedarf zu berechnen.
Bekannte und gemessene Eigenschaften sind:
a. Gasvolumenstrom (qS) oder Gasmassenstrom ()
b. Gaszusammensetzung (zi)
c. Ansaugdruck (P1) und -temperatur (T1)
d. Austrittsdruck (P2) und Temperatur (T2)
Wirkungsgradabschätzung – Strenge Methode
Das Herzstück jeder kommerziellen Software zur Simulation von Prozessabläufen ist eine Zustandsgleichung. Aufgrund ihrer Einfachheit und relativen Genauigkeit wird eine kubische EOS wie Soave Redlich-Kwong (SRK) oder Peng-Robinson verwendet. Diese Gleichungen werden zur Berechnung von Dampf-Flüssigkeits-Gleichgewichten (VLE), Enthalpie (h) und Entropie (s) verwendet. Mit den richtigen binären Wechselwirkungskoeffizienten sind die Prozesssimulationsergebnisse dieser beiden Gleichungen praktisch identisch. Daher wird in dieser Arbeit nur die SRK verwendet.
Der isentrope Wirkungsgrad ist definiert durch
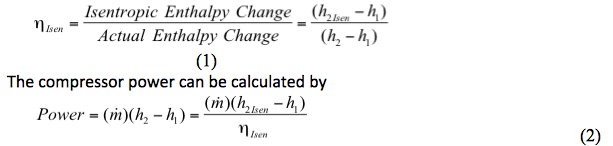
Wobei:
ηIsen = Isentropenwirkungsgrad
h1 = Ansaugenthalpie berechnet bei P1, T1, und Zusammensetzung (zi)
h2 = Ausstoßenthalpie berechnet bei P2, T2, und Zusammensetzung (zi)
h2Isen = Isentrope Austrittsenthalpie bei P2 (oder T2), S2Isen =S1, und Zusammensetzung (zi)
![]() = Massendurchsatz
= Massendurchsatz
Die Berechnung des Verdichterwirkungsgrades oder der Leistung umfasst zwei Schritte
1. Bestimmung der idealen oder isentropen (reversiblen und adiabatischen) Enthalpieänderung (h2Isen-h1) des Verdichtungsprozesses.
2. Bestimmung der tatsächlichen Enthalpieänderung (h2-h1).
Die schrittweise Berechnung auf Basis eines EOS:
a. Nehmen Sie einen stationären Zustand an, d.h.
b. Nehmen Sie an, dass die Zusammensetzung der Zufuhr unverändert bleibt
c. Berechnen Sie die Saugenthalpie h1=f(P1, T1 und zi) und die Entropie s1=f(P1, T1 und zi) nach EOS
d. Nehmen Sie einen isentropen Prozess an und setzen Sie s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Berechnen Sie die ideale Enthalpie (h2Isen) im Auslaufzustand bei bekanntem zi, T2 (oder P2) und s2Isen.
f. Berechnen Sie die tatsächliche Enthalpie (h2) im Entladungszustand für bekannte zi, T2 und P2.
g. Berechne den isentropen Wirkungsgrad nach Gleichung 1: µIsen = (h2Isen – h1)/(h2 – h1)
h. Berechnen Sie die Leistung nach Gleichung 2: ![]()
Schätzung des Wirkungsgrads – Shortcut-Methode
Der isentrope Wegexponent (k) oder das Verhältnis der Wärmekapazität des idealen Gases (k=CP/CV) kann anhand der in der TOTM vom Mai 2013 vorgestellten Korrelation berechnet werden:
![]()
Wobei:
T = Temperatur, K (°R)
![]() = Relative Dichte des Gases; Verhältnis von Gasmolekulargewicht zu Luftmolekulargewicht
= Relative Dichte des Gases; Verhältnis von Gasmolekulargewicht zu Luftmolekulargewicht
A = 0.000272 (0.000151)
Die tatsächliche Entladetemperatur auf der Grundlage eines isentropen Pfades kann geschätzt werden durch

Auflösen des isentropen Wirkungsgrades,
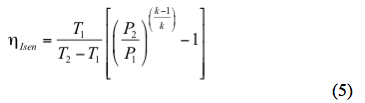
Analog, kann die tatsächliche Entladetemperatur auf der Grundlage eines polytropen Pfades geschätzt werden, indem

die obige Gleichung für den polytropen Pfadkoeffizienten (n) gelöst wird:

In ähnlicher Weise kann die tatsächliche Entladetemperatur auf der Grundlage eines polytropen Pfades geschätzt werden (ηPoly) durch:

Die isentrope Förderhöhe wird berechnet durch
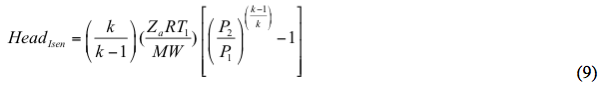
Ähnlich, die polytrope Förderhöhe wird berechnet durch
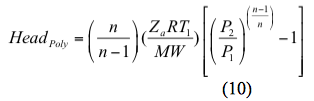
Für einen isentropen (reversiblen und adiabatischen) Prozess wird die Leistung berechnet durch
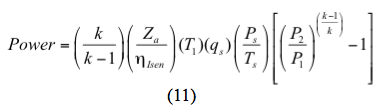
oder für einen polytropen Prozess wird die Leistung berechnet durch
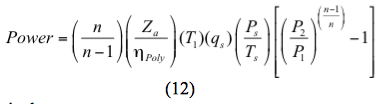
Alternativ:
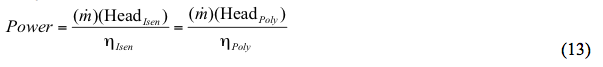
Wo:
Förderhöhe = Förderhöhe des Verdichters, m (ft)
Leistung = Leistung des Verdichters, kW (HP)
R = Universelle Gaskonstante, 848 kg-m/(kmol-K) oder (1545 ft-lbf/(lbmol-°R))
PS = Druck im Normalzustand, kPa (psia)
P1 = Ansaugdruck, kPa (psia)
P2 = Austrittsdruck, kPa (psia)
TS = Temperatur bei Standardbedingungen, K (°R)
T1 = Ansaugtemperatur, K (°R)
T2 = Austrittstemperatur, K (°R)
qS = Gasvolumenstrom bei Standardbedingungen, Sm3/d (scf/Tag)
Za = Mittlerer Gas-Kompressibilitätsfaktor = (Z1+Z2)/2
Z1 = Gas-Kompressibilitätsfaktor bei der Ansaugbedingung
Z2 = Gas-Kompressibilitätsfaktor bei der Ausstoßbedingung
MW = Molekulargewicht des Gases
Die Leistungsberechnung sollte für jede Verdichtungsstufe erfolgen und dann für alle an einen einzigen Treiber angeschlossenen Stufen summiert werden.
Die schrittweise Berechnung für die Abkürzungsmethode
a. Berechnen Sie den Isentropenexponenten (k) nach Gleichung 3 unter Verwendung der durch T = (T1+3T2)/4 definierten Durchschnittstemperatur. Diese Form der Durchschnittstemperatur wurde festgelegt, um eine bessere Übereinstimmung zwischen den Ergebnissen der strengen und der verkürzten Methode zu erzielen.
b. Berechnen Sie den isentropen Wirkungsgrad (ηIsen) nach Gleichung 5.
c. Berechne den polytropen Koeffizienten (n) nach Gleichung 7.
d. Berechne den polytropen Wirkungsgrad (ηPoly) nach Gleichung 8.
e. Berechnen Sie die isentrope und die polytrope Förderhöhe nach Gleichung 9 bzw. 10.
f. Berechnen Sie die erforderliche Leistung pro Stufe entweder mit Gleichung 11 oder 12.
Fallstudie
Ein Erdgasgemisch wird mit einem dreistufigen Zentrifugalkompressor verdichtet. Das Verfahrensfließbild ist in Abbildung 1 dargestellt. Für jede Stufe sind die gemessenen Drücke und Temperaturen in Tabelle 1 aufgeführt. Die gemessene Zusammensetzung des Einsatzmaterials, die Durchflussmengen sowie das berechnete Molekulargewicht und die relative Dichte sind in Tabelle 2 aufgeführt.
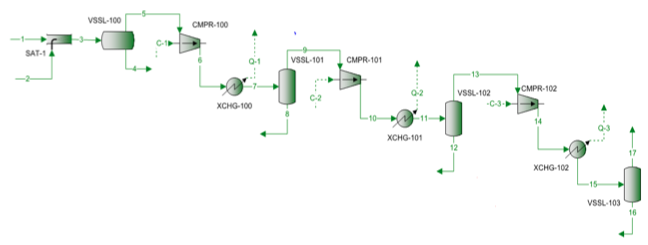
Abbildung 1. Verfahrensfließbild für eine 3-stufige Verdichtung
Tabelle 1. Gemessene Temperatur und Druck für die drei Stufen der Verdichtung
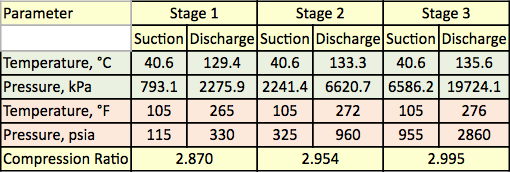
Tabelle 2. Gasanalyse und Durchflussmenge für die drei Verdichtungsstufen
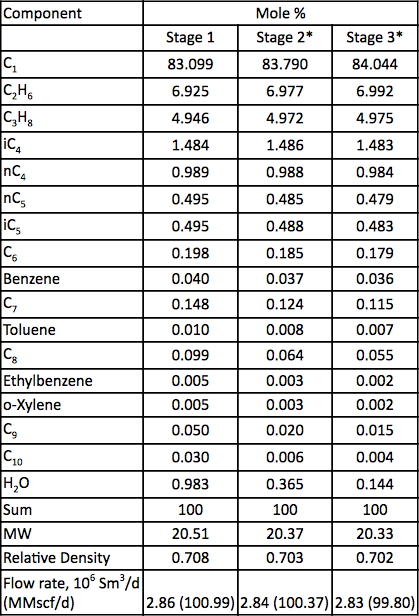
* Berechnet
Ergebnisse und Diskussionen
Das in Abbildung 1 gezeigte Prozessflussdiagramm wurde mit der Software ProMax simuliert, um die strengen Berechnungen mit dem SRK EOS durchzuführen. Das Programm berechnete polytrope und isentrope Wirkungsgrade, Förderhöhen und Verdichtungsleistungen. Das Programm berechnete auch den isentropen Wegexponenten (k) und den polytropen Wegexponenten (n). Diese Berechnungsergebnisse sind in Tabelle 2 für alle drei Stufen unter SRK-Rubriken aufgeführt. Die von ProMax durchgeführten Berechnungen ähneln sehr stark der im strengen Abschnitt beschriebenen schrittweisen Berechnung von a bis h. In Tabelle 2 sind auch die Ergebnisse der Shortcut-Berechnungen für die entsprechenden Werte unter der Shortcut-Überschrift aufgeführt. Die Abkürzungsberechnungen basieren auf der im Abschnitt über die Abkürzungsmethode beschriebenen schrittweisen Berechnung von a bis f. Die prozentualen Fehler zwischen der strengen Methode und den Abkürzungsmethoden für jede Stufe sind ebenfalls in Tabelle 2 aufgeführt. Tabelle 2 zeigt, dass für die Stufen 1 und 2 ausgezeichnete Übereinstimmungen erzielt werden. Größere Abweichungen werden jedoch für den isetropen und den polytropen Exponenten der Stufe 3 festgestellt, was auf den Hochdruckbetrieb zurückzuführen ist, der zu weit von den idealen Gaszustandsbedingungen abweicht.
Tabelle 3. Zusammenfassung der rigorosen und der mit der Abkürzung berechneten Ergebnisse
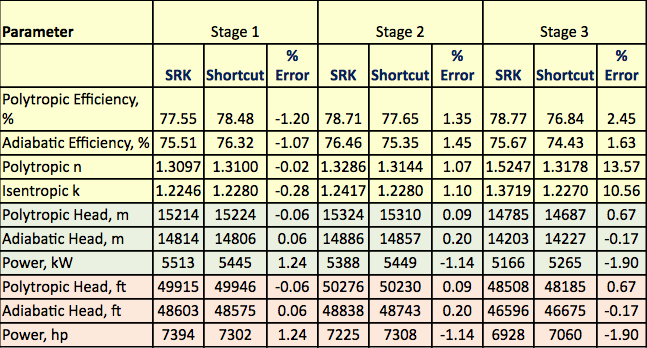
Schlussfolgerungen
Tabelle 2 zeigt, dass es gute Übereinstimmungen zwischen der Abkürzung und den rigorosen Ergebnissen gibt. Die Unterschiede zwischen den Ergebnissen der rigorosen und der Shortcut-Methode für die Berechnung von Anlagen und für Planungszwecke sind vernachlässigbar. Für Stufe 3 wird aufgrund des Hochdruckbetriebs und einer zu großen Abweichung vom idealen Gaszustand ein größerer Fehler für den Isentropenexponenten (k) beobachtet.
Der berechnete Isentropenexponent (k) in ProMax ist nicht das Verhältnis der Wärmekapazität im idealen Gaszustand (CP/CV). Es ist der Wert des Isentropenexponenten, der erforderlich ist, um einen isentropen Pfad vom Einlass zum Auslass zu erhalten. Sein Wert wird als Integration dieses Weges berechnet. Es handelt sich also gewissermaßen um einen „Durchschnittswert“, der den wahren isentropen Weg darstellt. Bei idealen Gasen wäre der Wert gleich dem (CP/CV)-Verhältnis.
Dieser Fehler bei „k“ zeigt auch, wie wichtig es ist, bei der Bestellung einer Leistungsprüfung anzugeben, welche Korrelation verwendet werden soll (d. h. weitere Einzelheiten sind in ASME PTC-10 zu finden), damit Kunde und Anbieter sich in Bezug auf Molekulargewicht (MW) und k für die Testflüssigkeit einig sind. Weitere Einzelheiten finden Sie in der Referenz und in den TOTMs vom August und September 2010.
Es ist auch erwähnenswert, dass bei der Entwicklung von ’n‘ und dem polytropen Wirkungsgrad zur Bewertung des Maschinenzustands die relative Genauigkeit der Messinstrumente/-ausrüstung (Temperatur- und Druckwandler) und die Abbildung der Kompressorleistung auf die ursprüngliche Leistungskurve (tatsächlicher Gasvolumenstrom im Verhältnis zur Drehzahl) viele potenzielle Fehlerquellen in diese tägliche Bewertung einbringen.
Beachten Sie, dass die Genauigkeit der Kurzschlussmethoden von den Werten von k und n abhängt. Die Definition der Durchschnittstemperatur in der Shortcut-Methode wurde angepasst, um eine bessere Übereinstimmung mit dem durch die rigorose Methode berechneten isentropen Pfadexponenten (k) zu erreichen.
Um mehr über ähnliche Fälle und die Minimierung von Betriebsproblemen zu erfahren, empfehlen wir die Teilnahme an unseren Kursen G4 (Gasaufbereitung und -verarbeitung), PF4 (Ölförder- und -verarbeitungsanlagen), ME46 (Kompressorsysteme – Mechanische Konstruktion und Spezifikationen) und ME44 (Grundlagen von Pumpen- und Kompressorsystemen).
PetroSkills bietet Beratungsleistungen zu diesem und vielen anderen Themen. Weitere Informationen zu diesen Dienstleistungen finden Sie auf unserer Website unter http://petroskills.com/consulting oder per E-Mail unter [email protected].
Dr. Mahmood Moshfeghian
Referenz:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, S. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, „Performance test Code on Compressors and Exhausters“, 1997.
7. Honeywell, J. „Wichtige Aspekte der Prüfung von Zentrifugalkompressoren – Teil 1“, Tipp des Monats, August 2010
8. Honeywell, J. „Wichtige Aspekte der Prüfung von Zentrifugalkompressoren – Teil 2“, Tipp des Monats, September 2010