Al igual que el controlador P-Only, el algoritmo Proporcional-Integral (PI) computa y transmite una señal de salida del controlador (CO) cada tiempo de muestreo, T, al elemento de control final (por ejemplo, válvula, bomba de velocidad variable). El CO calculado por el algoritmo PI está influenciado por los parámetros de ajuste del controlador y el error del controlador, e(t).
Los controladores PI tienen dos parámetros de ajuste. Aunque esto hace que sean más difíciles de ajustar que un controlador sólo P, no son tan complejos como el controlador PID de tres parámetros.
La acción integral permite a los controladores PI eliminar el desplazamiento, una de las principales debilidades de un controlador sólo P. Por lo tanto, los controladores PI proporcionan un equilibrio de complejidad y capacidad que los convierte, con diferencia, en el algoritmo más utilizado en las aplicaciones de control de procesos.
El Algoritmo PI
Mientras que diferentes vendedores presentan lo que es esencialmente el mismo algoritmo en diferentes formas, aquí exploramos lo que se describe diversamente como la forma dependiente, ideal, continua y de posición:
![]()
Donde:
CO = señal de salida del controlador (la salida del cable)
CObias = sesgo del controlador o valor nulo; establecido por la transferencia sin pelota como se explica a continuación
e(t) = error actual del controlador, definido como SP – PV
SP = punto de ajuste
PV = variable de proceso medida (el cable de entrada)
Kc = ganancia del controlador, un parámetro de ajuste
Ti = tiempo de restablecimiento, un parámetro de ajuste
Los dos primeros términos a la derecha del signo igual son idénticos al controlador P-Only al que se hace referencia en la parte superior de este artículo.
El modo integral del controlador es el último término de la ecuación. Su función es integrar o sumar continuamente el error del controlador, e(t), a lo largo del tiempo.
Algunas cosas que debemos saber sobre el parámetro de ajuste del tiempo de reajuste, Ti:
| ▪ | Proporciona un peso separado al término integral para que la influencia de la acción integral pueda ajustarse independientemente. |
| ▪ | Se encuentra en el denominador por lo que los valores más pequeños proporcionan un mayor peso a (es decir aumentar la influencia de) el término integral. |
| ▪ | Tiene unidades de tiempo por lo que siempre es positivo. |
Función del término proporcional
Al igual que con el controlador P-Only, el término proporcional del controlador PI, Kc-e(t), suma o resta de CObias basado en el tamaño del error del controlador e(t) en cada tiempo t.
Cuando e(t) crece o se reduce, la cantidad añadida a CObias crece o se reduce inmediata y proporcionalmente. La historia pasada y la trayectoria actual del error del controlador no influyen en el cálculo del término proporcional.
El gráfico siguiente (haga clic para verlo en grande) ilustra esta idea para una respuesta de punto de ajuste. El error utilizado en el cálculo proporcional se muestra en el gráfico:
▪ En el tiempo t = 25 min, e(25) = 60-56 = 4
▪ En el tiempo t = 40 min, e(40) = 60-62 = -2
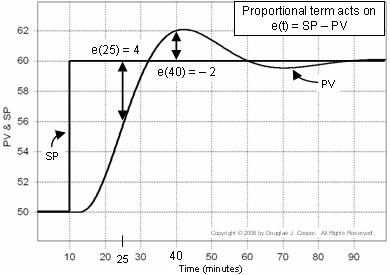
Recordando que el error del controlador e(t) = SP – PV, en lugar de ver PV y SP como trazas separadas como hacemos arriba, podemos calcular y trazar e(t) en cada punto del tiempo t.
Abajo (haga clic para una vista grande) son los datos idénticos a los de arriba sólo que se refunden como un gráfico de e(t) sí mismo. Observe que en el gráfico de arriba, PV = SP = 50 para los primeros 10 minutos, mientras que en el gráfico de error de abajo, e(t) = 0 para el mismo período de tiempo.
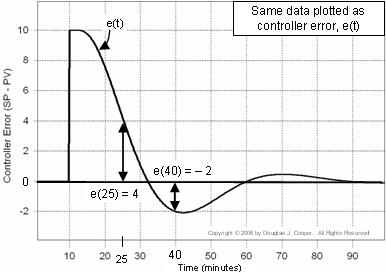
Este gráfico es útil ya que nos ayuda a visualizar cómo el error del controlador cambia continuamente de tamaño y signo a medida que pasa el tiempo.
Función del término integral
Mientras que el término proporcional considera el tamaño actual de e(t) sólo en el momento del cálculo del controlador, el término integral considera la historia del error, o cuánto tiempo y cuánto se ha alejado la variable de proceso medida del punto de consigna a lo largo del tiempo.
La integración es una suma continua. La integración del error a lo largo del tiempo significa que sumamos el historial completo de errores del controlador hasta el momento actual, empezando por el momento en que el controlador se puso en automático.
El error del controlador es e(t) = SP – PV. En el gráfico siguiente (haga clic para verlo en grande), la suma integral del error se calcula como las áreas sombreadas entre las trazas de SP y PV.
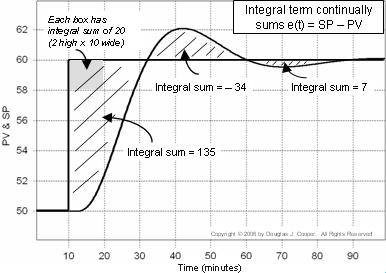
Cada caja del gráfico tiene una suma integral de 20 (2 de alto por 10 de ancho). Si contamos el número de cajas (incluyendo fracciones de cajas) contenidas en las áreas sombreadas, podemos calcular la suma integral del error.
Así que cuando el PV cruza por primera vez el punto de ajuste alrededor de t = 32, la suma integral ha crecido hasta aproximadamente 135. Escribimos el término integral del controlador PI como:
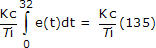
Dado que es el error del controlador el que impulsa el cálculo, obtenemos una visión directa de la situación a partir de un gráfico de error del controlador como el que se muestra a continuación (haga clic para verlo en grande):

Note que la integral de cada porción sombreada tiene el mismo signo que el error. Dado que la suma integral comienza a acumularse cuando el controlador se pone en automático por primera vez, la suma integral total crece mientras e(t) es positiva y se reduce cuando es negativa.
En el tiempo t = 60 min en los gráficos, la suma integral es 135 – 34 = 101. La respuesta se resuelve en gran medida en t = 90 min, y la suma integral es entonces 135 – 34 + 7 = 108.
La acción integral elimina el desplazamiento
La frase anterior hace una observación sutil pero muy importante. La respuesta es en gran parte completa en el tiempo t = 90 min, sin embargo la suma integral de todo el error no es cero.
En este ejemplo, la suma integral tiene un valor final o residual de 108. Es este valor residual el que permite la acción integral del controlador PI para eliminar el offset.
Como se discutió en un artículo anterior, la mayoría de los procesos bajo control sólo P experimentan offset durante la operación normal. El offset es un valor sostenido para el error del controlador (es decir, PV no es igual a SP en estado estacionario).
Reconocemos del controlador P-Only:
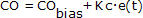
que CO siempre será igual a CObias a menos que le sumemos o restemos algo.
La única forma en que tenemos algo que sumar o restar de CObias en la ecuación P-Only anterior es si e(t) no es cero. Si e(t) no es estable en cero, entonces PV no es igual a SP y tenemos desplazamiento.
Sin embargo, con el controlador PI:
![]()
ahora sabemos que la suma integral de error puede tener un valor final o residual después de que se complete una respuesta. Esto es importante porque significa que e(t) puede ser cero, y aun así podemos tener algo que sumar o restar a CObias para formar la salida final del controlador, CO.
Así que mientras haya algún error (mientras e(t) no sea cero), el término integral crecerá o se reducirá en tamaño para impactar en CO. Los cambios en CO sólo cesarán cuando PV sea igual a SP (cuando e(t) = 0) durante un período de tiempo sostenido.
En ese momento, el término integral puede tener un valor residual como se acaba de discutir. Este valor residual de la integración, cuando se añade a CObias, crea esencialmente un nuevo valor de sesgo global que corresponde al nuevo nivel de operación.
En efecto, la acción integral restablece continuamente el valor de sesgo para eliminar el desplazamiento a medida que cambia el nivel de operación.
Desafíos del control PI
Existen desafíos al emplear el algoritmo PI:
| ▪ | Los dos parámetros de ajuste interactúan entre sí y su influencia debe ser equilibrada por el diseñador. |
| ▪ | El término integral tiende a aumentar el comportamiento oscilatorio o de balanceo de la respuesta del proceso. |
Debido a que los dos parámetros de sintonía interactúan entre sí, puede ser un reto llegar a los «mejores» valores de sintonía. El valor y la importancia de nuestro diseño y la receta de sintonía aumentan a medida que el controlador se vuelve más complejo.
Inicialización del controlador para la transferencia sin baches
Cuando cambiamos cualquier controlador de modo manual a automático (de bucle abierto a bucle cerrado), queremos que el resultado sea sin problemas. Es decir, no queremos que la conmutación cause acciones de control abruptas que impacten o interrumpan nuestro proceso
Logramos este resultado deseado en la conmutación inicializando la suma integral de error del controlador a cero. Además, el punto de consigna y el valor de sesgo del controlador se inicializan estableciendo:
▪ SP igual al PV actual
▪ CObias igual al CO actual
Con la suma integral de error ajustada a cero, no hay nada que sumar o restar a CObias que pueda causar un cambio repentino en la salida actual del controlador. Con el punto de ajuste igual a la variable de proceso medida, no hay ningún error que impulse un cambio en nuestro CO. Y con el sesgo del controlador ajustado a nuestro valor actual de CO, estamos preparados por defecto para mantener el funcionamiento actual.
Así, cuando cambiamos del modo manual al automático, tenemos una «transferencia sin obstáculos» sin sorpresas. Este es un resultado que todo el mundo aprecia.
Tiempo de reajuste frente a velocidad de reajuste
Los distintos proveedores presentan sus algoritmos de control de formas ligeramente diferentes. Algunos utilizan la banda proporcional en lugar de la ganancia del controlador. Además, algunos utilizan la tasa de reposición, Tr, en lugar del tiempo de reposición. Estos son simplemente la inversa de cada uno:
Tr = 1/Ti
No importa cómo se expresen los parámetros de sintonía, los algoritmos PI son todos igualmente capaces.
Pero es crítico conocer a su fabricante antes de comenzar a sintonizar su controlador porque los valores de los parámetros deben coincidir con su forma particular de algoritmo.El software comercial para el diseño y la sintonización del controlador resolverá automáticamente este problema por usted.
Implementación de un controlador PI
Exploramos el diseño, la sintonización y la implementación del controlador PI en el intercambiador de calor en este artículo y en los tanques drenados por gravedad en este artículo.