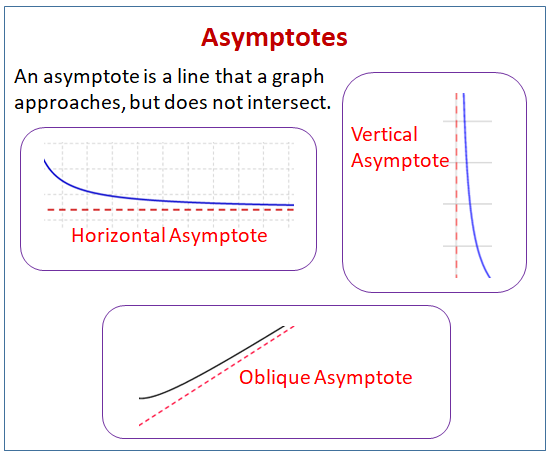
Una asíntota es una línea a la que se aproxima una gráfica, pero que no la interseca.
En esta lección, aprenderemos a encontrar las asíntotas verticales, las asíntotas horizontales y las asíntotas oblicuas (inclinadas) de las funciones racionales.
Temas relacionados:
Más lecciones sobre Cálculo

El siguiente diagrama muestra los diferentes tipos de asíntotas: asíntotas horizontales, asíntotas verticales y asíntotas oblicuas. Desplázate hacia abajo en la página para ver más ejemplos y soluciones sobre cómo encontrar asíntotas.

¿Cómo determinar la Asíntota Vertical?

Método 1: Usar la Definición de Asíntota Vertical

La recta x = a se llama Asíntota Vertical de la curva y = f(x) si al menos una de las siguientes afirmaciones es verdadera.

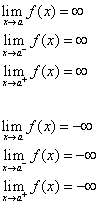
Método 2:

Para las funciones racionales, las asíntotas verticales son líneas verticales que corresponden a los ceros del denominador.
Dada la función racional, f(x)

Paso 1: escribir f(x) en forma reducida

Paso 2: si x – c es un factor en el denominador entonces x = c es la asíntota vertical.

Ejemplo:

Hallar las asíntotas verticales de

Solución:

Método 1: Utilizar la definición de Asíntota Vertical.

Si x es cercana a 3 pero mayor que 3, entonces el denominador x – 3 es un número positivo pequeño y 2x es cercano a 8. Entonces, es un número positivo grande.

Intuitivamente, vemos que

De manera similar, si x está cerca de 3 pero es menor que 3, entonces x – 3 es un número negativo pequeño y 2x está cerca de 8. Entonces, es un número negativo grande.

La recta x = 3 es la asíntota vertical.

Método 2:

Paso 1: f(x) ya está en forma reducida.

Paso 2: El denominador es x – 3, y por tanto la Asíntota Vertical está en x = 3.

Encontrar las asíntotas verticales de las funciones racionales

Qué buscar, para encontrar las asíntotas verticales de las funciones racionales.

• Mostrar soluciones paso a paso

Asíntotas verticales de las funciones racionales: Manera rápida de encontrarlas

Ejemplo de encontrar asíntotas verticales de funciones racionales.

• Mostrar soluciones paso a paso

¿Cómo encontrar asíntotas verticales de funciones racionales

• Mostrar soluciones paso a paso

Cómo determinar la Asíntota horizontal?

Método 1: Utilizar la definición de Asíntota Horizontal

La recta y = L se llama asíntota horizontal de la curva y = f(x) si

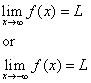
Método 2:

Para la función racional, f(x)

Si el grado de x en el numerador es menor que el grado de x en el denominador entonces y = 0 es la asíntota horizontal.

Si el grado de x en el numerador es igual al grado de x en el denominador entonces y = c donde c se obtiene dividiendo los coeficientes principales.

Ejemplo:

Hallar las asíntotas horizontales y verticales de la función.

Solución:

Método 1:

Dividir tanto el numerador como el denominador por x.

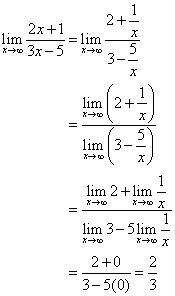
La recta es la asíntota horizontal.

Método 2:

El grado de x en el numerador es igual al grado de x en el denominador.

Dividiendo los coeficientes principales obtenemos

La recta es la asíntota horizontal.

Ahorro para encontrar las asíntotas horizontales de las funciones racionales

Un par de trucos que hacen que encontrar las asíntotas horizontales de las funciones racionales sea muy fácil de hacer

• Mostrar soluciones paso a paso

Este vídeo dará una visión básica de las asíntotas horizontales. Determinaremos si las funciones racionales dadas tienen asíntotas horizontales y cuáles son.

• Mostrar soluciones paso a paso

En este vídeo se profundizará en las reglas de las asíntotas horizontales.

• Mostrar soluciones paso a paso

Asíntota oblicua o asíntota inclinada

Algunas curvas tienen asíntotas que son oblicuas, es decir, ni horizontales ni verticales.

Si entonces la recta y = mx + b se llama asíntota oblicua o inclinada porque las distancias verticales entre la curva y = f(x) y la recta y = mx + b se aproximan a 0.

Para las funciones racionales, las asíntotas oblicuas se producen cuando el grado del numerador es uno más que el grado del denominador. En tal caso, la ecuación de la asíntota oblicua se puede encontrar por división larga.

Ejemplo:

Hallar las asíntotas de la función

Solución:

Como el denominador x2 + 1 nunca es 0, no hay asíntota vertical.

Como el grado de x en el numerador es mayor que el grado de x en el denominador no hay asíntota horizontal.

Como el grado de x en el numerador es uno mayor que el grado de x en el denominador podemos utilizar la división larga para obtener la asíntota oblicua.

Así pues, la recta y = x es la asíntota oblicua.

Encontrando asíntotas oblicuas de funciones racionales

Este vídeo describe cuándo una función racional tiene una asíntota oblicua, describe brevemente qué es una asíntota oblicua y luego hace dos ejemplos.

• Mostrar soluciones paso a paso

Hallar las asíntotas de una función racional (verticales, horizontales y oblicuas/escalonadas)

Este vídeo muestra cómo hallar las asíntotas verticales y las asíntotas oblicuas/escalonadas de una función racional.

• Mostrar soluciones paso a paso

Hallar todas las asíntotas de una función racional (verticales, horizontales, oblicuas / inclinadas)

Aquí observamos una función y hallamos la asíntota vertical y también concluimos que no hay asíntotas horizontales, pero que sí existe una asíntota oblicua. Entonces usamos la división larga para encontrar la asíntota oblicua.

• Mostrar soluciones paso a paso

Prueba la calculadora gratuita de Mathway y el solucionador de problemas de abajo para practicar varios temas de matemáticas. Prueba los ejemplos dados, o escribe tu propio problema y comprueba tu respuesta con las explicaciones paso a paso.