La identidad de Euler parece desconcertante:
![]()
Surge de una fórmula más general:
![]()
Yowza — ¡estamos relacionando un exponente imaginario con el seno y el coseno! Y de alguna manera al enchufar pi da -1? ¿Podría ser esto intuitivo?
No según el matemático de 1800 Benjamin Peirce:
Es absolutamente paradójico; no podemos entenderlo, y no sabemos lo que significa, pero lo hemos probado, y por lo tanto sabemos que debe ser la verdad.
¡Argh, esta actitud me hace hervir la sangre! Las fórmulas no son hechizos mágicos que hay que memorizar: debemos, debemos, encontrar una visión. Aquí está la mía:
La fórmula de Euler describe dos formas equivalentes de moverse en un círculo.
¿Eso es todo? ¿Esta asombrosa ecuación trata de girar alrededor? Sí — y podemos entenderla basándonos en algunas analogías:
- Comenzando por el número 1, veamos la multiplicación como una transformación que cambia el número: $1 \cdot e^{i \pi}$
- El crecimiento exponencial regular aumenta continuamente 1 en alguna tasa durante algún período de tiempo; el crecimiento exponencial imaginario gira continuamente 1 durante algún período de tiempo
- Crecer por unidades de tiempo «pi» significa dar pi radianes alrededor de un círculo
- Por lo tanto, $e^{i \pi}$ significa empezar en 1 y girar pi (la mitad de un círculo) para llegar a -1
Esa es la visión de alto nivel, vamos a sumergirnos en los detalles. Por cierto, si alguien intenta impresionarte con $e^{i \pi} = -1$, pregúntale por i a la i-ésima potencia. Si no son capaces de pensarlo, la fórmula de Euler sigue siendo un hechizo mágico para ellos.
Actualización: Mientras escribía, pensé que un vídeo podría ayudar a explicar las ideas con más claridad:
Entendiendo cos(x) + i * sin(x)
El signo de igual está sobrecargado. A veces queremos decir «poner una cosa en otra» (como x = 3) y otras queremos decir «estas dos cosas describen el mismo concepto» (como $\sqrt{-1} = i$).
La fórmula de Euler es esto último: da dos fórmulas que explican cómo moverse en una circunferencia. Si examinamos el movimiento circular utilizando la trigonometría, y recorriendo x radianes:
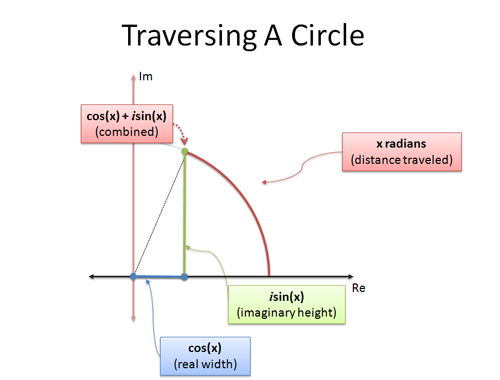
- cos(x) es la coordenada x (distancia horizontal)
- sin(x) es la coordenada y (distancia vertical)
La afirmación
![]()
es una forma inteligente de aplastar las coordenadas x e y en un solo número. La analogía «los números complejos son bidimensionales» nos ayuda a interpretar un único número complejo como una posición en una circunferencia.
Cuando fijamos x en $\pi$, estamos viajando $\pi$ unidades a lo largo del exterior del círculo unitario. Como la circunferencia total es de $2\pi$, el viejo $\pi$ está a mitad de camino, situándonos en -1.
Neato: El lado derecho de la fórmula de Euler ($\cos(x) + i \sin(x)$) describe el movimiento circular con números imaginarios. Ahora vamos a averiguar cómo el lado e de la ecuación lo logra.
¿Qué es el crecimiento imaginario?
Combinar las coordenadas x e y en un número complejo es complicado, pero manejable. Pero, ¿qué significa un exponente imaginario?
Vamos a retroceder un poco. Cuando veo $3^4$, pienso en ello así:
- 3 es el resultado final de crecer instantáneamente (usando e) a un ritmo de ln(3). En otras palabras: $3 = e^{ln(3)}$
- $3^4$ es lo mismo que crecer hasta 3, pero creciendo durante 4 veces más. Así que $3^4 = e^{\ln(3) \cdot 4} = 81$
En lugar de ver los números por sí mismos, se puede pensar en ellos como algo a lo que e tuvo que «crecer». Los números reales, como el 3, dan una tasa de interés de ln(3) = 1,1, y eso es lo que e «recoge» a medida que avanza, creciendo continuamente.
El crecimiento regular es sencillo: sigue «empujando» un número en la misma dirección real en la que iba. 3 × 3 empuja en la dirección original, haciéndolo 3 veces más grande (9).
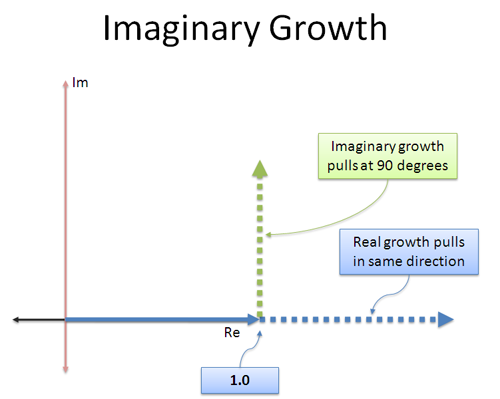
El crecimiento imaginario es diferente: ¡el «interés» que ganamos va en otra dirección! Es como un motor a reacción que se ató de lado — en lugar de ir hacia adelante, empezamos a empujar a 90 grados.
Lo bueno de un empuje ortogonal (perpendicular) constante es que no te acelera ni te frena — ¡te hace girar! Tomar cualquier número y multiplicarlo por i no cambiará su magnitud, sólo la dirección a la que apunta.
Intuitivamente, así es como veo la tasa de crecimiento imaginaria continua: «Cuando crezca, no me empujes hacia delante o hacia atrás en la dirección en la que ya voy. En su lugar, gíreme».
¿Pero no deberíamos girar cada vez más rápido?
Yo también me lo preguntaba. El crecimiento regular se compone en nuestra dirección original, así que vamos 1, 2, 4, 8, 16, multiplicando 2x cada vez y permaneciendo en los números reales. Podemos considerar esto $e^{\ln(2)x}$, lo que significa crecer instantáneamente a una tasa de ln(2) durante «x» segundos.
Y oye — si nuestra tasa de crecimiento fuera el doble de rápida, 2ln(2) vs ln(2), parecería lo mismo que crecer durante el doble de tiempo (2x vs x). La magia de e nos permite intercambiar tasa y tiempo; 2 segundos a ln(2) es el mismo crecimiento que 1 segundo a 2ln(2).
Ahora, imaginemos que tenemos alguna tasa de crecimiento puramente imaginaria (Ri) que nos hace girar hasta alcanzar i, o 90 grados hacia arriba. ¿Qué sucede si duplicamos esa tasa a 2Ri, giraremos fuera del círculo?
¡No! Tener una tasa de 2Ri significa que simplemente giramos el doble de rápido, o alternativamente, giramos a una tasa de R durante el doble de tiempo, pero nos mantenemos en el círculo. Girar el doble de tiempo significa que ahora estamos orientados 180 grados.
Una vez que nos damos cuenta de que alguna tasa de crecimiento exponencial puede llevarnos de 1 a i, aumentar esa tasa sólo nos hace girar más. Nunca saldremos del círculo.
Sin embargo, si nuestra tasa de crecimiento es compleja (a+bi frente a Ri) entonces la parte real (a) nos hará crecer de forma normal, mientras que la parte imaginaria (bi) nos hace girar. Pero no nos compliquemos: La fórmula de Euler, $e^{ix}$, tiene que ver con el crecimiento puramente imaginario que nos mantiene en el círculo (más adelante).
Una rápida comprobación de cordura
Mientras escribía, tuve que aclararme algunas cuestiones:
¿Por qué usar $e^x$, no estamos rotando el número 1?
e representa el proceso de empezar en 1 y crecer continuamente al 100% de interés durante 1 unidad de tiempo.
Cuando escribimos e estamos capturando todo ese proceso en un solo número — e representa todo el engranaje del crecimiento continuo. Así que realmente, $e^x$ está diciendo «empieza en 1 y crece continuamente al 100% durante x segundos», y empieza desde 1 como queremos.
¿Pero qué hace i como exponente?
Para un exponente regular como $3^4$ preguntamos:
- ¿Cuál es la tasa de crecimiento implícita? Estamos creciendo de 1 a 3 (la base del exponente).
- ¿Cómo cambiamos esa tasa de crecimiento? La escalamos por 4x (la potencia del exponente).
Podemos convertir nuestro crecimiento en formato «e»: nuestra tasa instantánea es ln(3), y la aumentamos a ln(3) * 4. De nuevo, la potencia del exponente (4) acaba de escalar nuestra tasa de crecimiento.
![]()
Cuando el exponente superior es i (como en $3^i$), simplemente multiplicamos nuestra tasa de crecimiento implícita por i. Así que en lugar de crecer a ln(3), estamos creciendo a ln(3) * i.
![]()
La parte superior del exponente modifica la tasa de crecimiento implícita de la parte inferior.
Los detalles de la cuestión
Veamos más de cerca. Recuerde esta definición de e:
![]()
Que $\frac{100\%}{n}$ representa la porción de interés que ganamos en cada período microscópico. Asumimos que el tipo de interés era del 100% en la dimensión real – pero ¿qué pasaría si fuera del 100% en la dirección imaginaria?
![]()
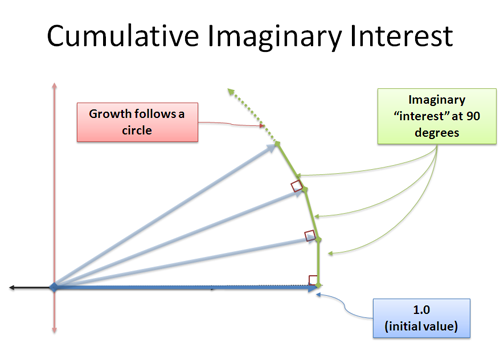
Ahora, nuestro interés recién formado se nos suma en la dirección de 90 grados. Sorprendentemente, esto no cambia nuestra longitud – este es un concepto complicado, porque parece hacer un triángulo donde la hipotenusa debe ser mayor. Estamos tratando con un límite, y la distancia extra está dentro del margen de error que especificamos. Esto es algo que quiero abordar otro día, pero hazme caso: el crecimiento perpendicular continuo te hará girar. Este es el corazón de seno y coseno, donde su cambio es perpendicular a su posición actual, y se mueve en un círculo.
Aplicamos i unidades de crecimiento en incrementos infinitamente pequeños, cada uno empujándonos en un ángulo de 90 grados. No hay una rotación «cada vez más rápida» – en su lugar, nos arrastramos a lo largo del perímetro una distancia de |i| = 1 (magnitud de i).
Y oye — ¡la distancia arrastrada alrededor de un círculo es un ángulo en radianes! Hemos encontrado otra forma de describir el movimiento circular!
Para obtener el movimiento circular: Cambiar continuamente girando en un ángulo de 90 grados (también conocido como tasa de crecimiento imaginario).
Entonces, la fórmula de Euler está diciendo «el crecimiento exponencial e imaginario traza un círculo». Y esta trayectoria es la misma que se mueve en un círculo utilizando el seno y el coseno en el plano imaginario.
En este caso, la palabra «exponencial» es confusa porque viajamos alrededor del círculo a una tasa constante. En la mayoría de las discusiones, se supone que el crecimiento exponencial tiene un efecto acumulativo y compuesto.
Algunos ejemplos
No me crees realmente, ¿verdad? Aquí tienes unos cuantos ejemplos, y cómo pensar en ellos intuitivamente.
Ejemplo: $e^i$
¿Dónde está la x? Ah, es sólo 1. Intuitivamente, sin sacar una calculadora, sabemos que esto significa «recorrer 1 radián a lo largo del círculo unitario». En mi cabeza, veo que «e» intenta crecer 1 al 100% todo en la misma dirección, pero i sigue moviendo la bola y obliga a «1» a crecer a lo largo del borde del círculo:
![]()
No es el número más bonito, pero ahí está. Recuerda poner tu calculadora en modo radián cuando introduzcas esto.
Ejemplo: $3^i$
Esto es complicado — no está en nuestro formato estándar. Pero recuerde, ![]()
Queremos un crecimiento inicial de 3x al final del período, o una tasa instantánea de ln(3). Pero, llega la i y cambia esa tasa de ln(3) a «i * ln(3)»:
![]()
Pensábamos que nos íbamos a transformar a una tasa regular de ln(3), un poco más rápida que el 100% de crecimiento continuo ya que e es aproximadamente 2,718. Pero oh no, nos he hecho girar: ahora nos estamos transformando a una tasa imaginaria, lo que significa que sólo estamos girando. Si i fuera un número regular como 4, nos habría hecho crecer 4 veces más rápido. Ahora estamos creciendo a una velocidad de ln(3), pero lateralmente.
Deberíamos esperar un número complejo en el círculo unitario — no hay nada en la tasa de crecimiento para aumentar nuestro tamaño. Resolviendo la ecuación:
![]()
Así que, en lugar de acabar «1» unidad alrededor del círculo (como $e^i$) acabamos ln(3) unidades alrededor.
Ejemplo: $i^i$
Hace unos meses, esto me habría hecho llorar. Hoy no. Desglosemos las transformaciones:
![]()
Empezamos con 1 y queremos cambiarlo. Como resolver $3^i$, ¿cuál es la tasa de crecimiento instantánea representada por i como base?
Hrm. Normalmente haríamos ln(x) para obtener la tasa de crecimiento necesaria para alcanzar x al final de 1 unidad de tiempo. ¿Pero para una tasa imaginaria? Tenemos que hacer un poco de ruido.
Para empezar con 1 y crecer hasta i tenemos que empezar a girar desde el principio. ¿Cómo de rápido? Bueno, necesitamos conseguir 90 grados (pi/2 radianes) en 1 unidad de tiempo. Así que nuestra tasa es $i \frac{\pi}{2}$. Recuerda que nuestra velocidad debe ser imaginaria, ya que estamos girando, no creciendo. El viejo $\frac{\pi}{2}$ es aproximadamente 1,57 y resulta en un crecimiento regular.
Esto debería tener sentido: para convertir 1,0 en i al final de 1 unidad, deberíamos rotar $\frac{\pi}{2}$ radianes (90 grados) en esa cantidad de tiempo. Así, para obtener «i» podemos utilizar $e^{i \frac{pi}{2}$.
![]()
Phew. Eso describe a i como base. ¿Qué hay del exponente?
Bueno, la otra i nos dice que cambiemos nuestra velocidad — ¡sí, esa velocidad que pasamos tanto tiempo calculando! Así que en lugar de girar a una velocidad de $i \frac{\pi}{2}$, que es lo que significa una base de i, transformamos la tasa a:
![]()
¡Las i se cancelan y hacen que la tasa de crecimiento sea real de nuevo! Giramos nuestra tasa y nos empujamos a los números negativos. Y una tasa de crecimiento negativa significa que estamos encogiendo — deberíamos esperar que $i^i$ haga las cosas más pequeñas. Y lo hace:
![]()
¡Tada! (Busca «i^i» en Google para usar su calculadora)
Toma un respiro: Puedes intuir cómo deben comportarse las bases imaginarias y los exponentes imaginarios. Vaya.
Y como bonus, has averiguado ln(i) — para hacer que $e^x$ se convierta en i, haz que e gire $\frac{{pi}{2}$ radianes.
![]()
Ejemplo: (i^i)^i
¿Un doble exponente imaginario? Si insiste. En primer lugar, sabemos cuál será nuestra tasa de crecimiento dentro del paréntesis:
![]()
Obtenemos una tasa de crecimiento negativa (decreciente) de -pi/2. Y ahora volvemos a modificar esa tasa en i:
![]()
¡Y ahora tenemos una rotación negativa! Estamos dando una vuelta al círculo a una tasa de $-\frac{\pi}{2}$ por unidad de tiempo. ¿Cuánto tiempo vamos a ir? Bueno, hay un implícito «1» unidad de tiempo en la parte superior de esta cadena de exponentes; el defecto implícito es ir por 1 unidad de tiempo (al igual que $e = e^1$). 1 unidad de tiempo nos da una rotación de $-\frac{\pi}{2}$ radianes (-90 grados) o -i!
![]()
Y, sólo por diversión, si elevamos al cuadrado ese resultado loco:
![]()
Es «sólo» el doble de la rotación: 2 es un número regular por lo que duplica nuestra tasa de rotación a un completo -180 grados en una unidad de tiempo. O bien, puedes verlo como la aplicación de una rotación de -90 grados dos veces seguidas.
A primera vista, estos son exponentes realmente extraños. Pero con nuestras analogías podemos tomarlos con calma.
Crecimiento complejo
Podemos tener crecimiento real e imaginario al mismo tiempo: la parte real nos escala, y la parte imaginaria nos rota:
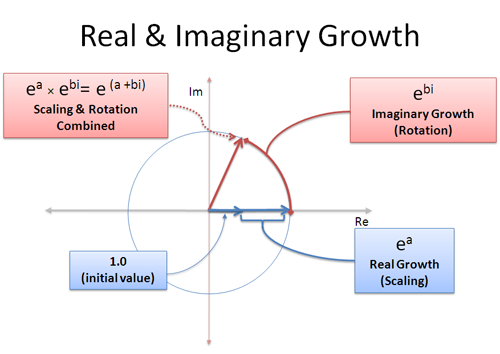
Una tasa de crecimiento complejo como (a + bi) es una mezcla de crecimiento real e imaginario. La parte real a, significa «crecer al 100% durante a segundos» y la parte imaginaria b significa «rotar durante b segundos». Recuerda que las rotaciones no obtienen el beneficio de la capitalización ya que sigues «empujando» en una dirección diferente — la rotación se suma linealmente.
¡Con esto en mente, podemos representar cualquier punto en un círculo de cualquier tamaño usando (a+bi)! El radio es $e^a$ y el ángulo está determinado por $e^{bi}$. Es como poner el número en el expansor durante dos ciclos: una vez para que crezca hasta el tamaño adecuado (a segundos), otra vez para rotarlo hasta el ángulo adecuado (b segundos). O bien, ¡podría rotarlo primero y luego crecer!
Digamos que queremos saber la cantidad de crecimiento para llegar a 6 + 8i. Esto es realmente pedir el logaritmo natural de un número imaginario: ¿cómo crecer e para obtener (6 + 8i)?
- Radio: ¿Cómo de grande es el círculo que necesitamos? Bueno, la magnitud es $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Lo que significa que necesitamos crecer durante ln(10) = 2,3 segundos para alcanzar esa cantidad.
- Cantidad a girar: ¿Cuál es el ángulo de ese punto? Podemos usar arctan para averiguarlo: atan(8/6) = 53 grados = .93 radianes.
- Combina el resultado: ln(6+8i) = 2,3 + .93i
Es decir, podemos alcanzar el punto aleatorio (6 + 8i) si usamos $e^{2.3 + .93i}$.
¿Por qué es útil?
La fórmula de Euler nos da otra forma de describir el movimiento en un círculo. Pero ya podíamos hacerlo con el seno y el coseno, ¿qué tiene de especial?
Todo es cuestión de perspectiva. El seno y el coseno describen el movimiento en términos de una cuadrícula, trazando coordenadas horizontales y verticales.

La fórmula de Euler utiliza coordenadas polares — ¿cuál es su ángulo y su distancia? De nuevo, son dos formas de describir el movimiento:
- Sistema de cuadrícula: Ir 3 unidades al este y 4 unidades al norte
- Coordenadas polares: Ir 5 unidades en un ángulo de 53,13 grados
Dependiendo del problema, las coordenadas polares o rectangulares son más útiles. La fórmula de Euler nos permite convertir entre las dos para utilizar la mejor herramienta para el trabajo. Además, como $e^{ix}$ se puede convertir en seno y coseno, podemos reescribir las fórmulas en trigonometría como variaciones de e, lo que resulta muy útil (no hace falta memorizar sin(a+b), se puede derivar — más otro día). Y es hermoso que cada número, real o complejo, sea una variación de e.
Pero utilidad, schmutilidad: el resultado más importante es la comprensión de que las ecuaciones desconcertantes pueden volverse intuitivas con las analogías adecuadas. No dejes que bellas ecuaciones como la fórmula de Euler sigan siendo un hechizo mágico – construye sobre las analogías que conoces para ver las ideas dentro de la ecuación.
Felices matemáticas.
Apéndice
El screencast fue divertido, y los comentarios son definitivamente bienvenidos. Creo que ayuda a las ideas pop, y caminando a través del artículo me ayudó a encontrar las lagunas en mi intuición.
- Brian Slesinsky tiene una presentación aseado en la fórmula de Euler
- Visual Análisis Complejo tiene una gran discusión sobre la fórmula de Euler – ver p. 10 en la vista previa del libro de Google
- Hice una charla sobre Matemáticas y Analogías que explica la identidad de Euler más visualmente:
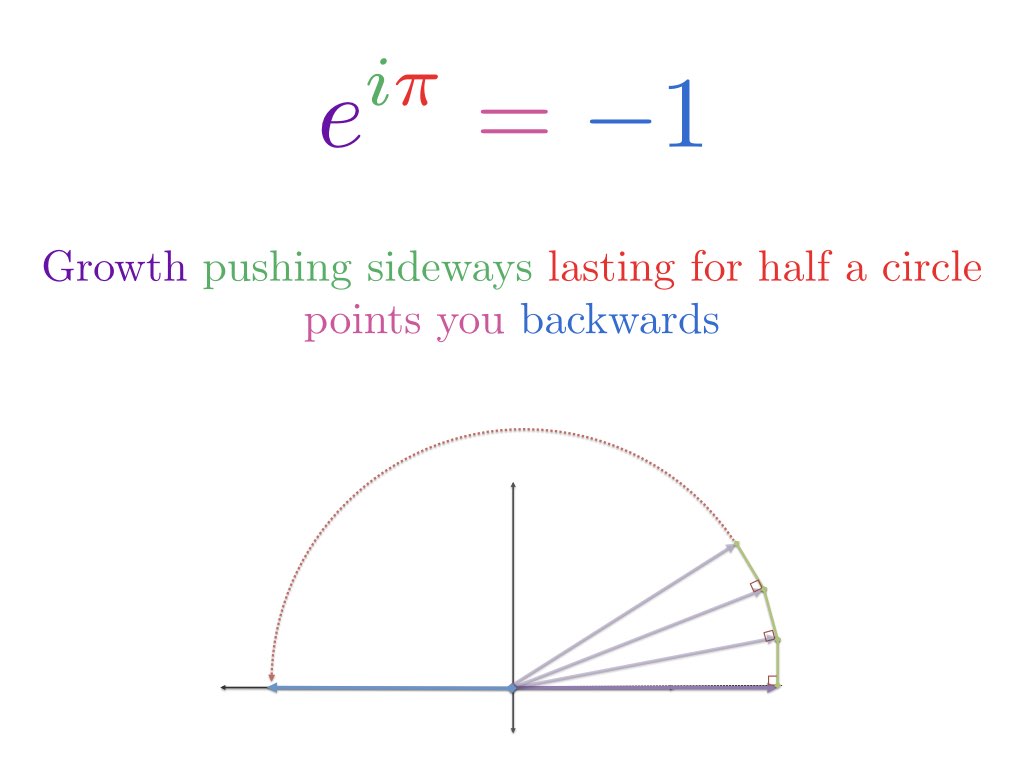
Otros posts de esta serie
- Una guía visual e intuitiva de los números imaginarios
- Aritmética intuitiva con números complejos
- Entender por qué funciona la multiplicación compleja
- Guía intuitiva de ángulos, Grados y radianes
- Comprensión intuitiva de la fórmula de Euler
- Guía interactiva de la transformada de Fourier
- Guía intuitiva de la convolución
- Entendimiento intuitivo de las ondas sinusoidales
- Guía intuitiva del álgebra lineal
- Intuición de un programador para la multiplicación de matrices
- Multiplicación imaginaria vs. Exponentes imaginarios