En el tip del mes de noviembre de 2011 (TOTM) presentamos los cálculos del compresor de un caso de estudio. Comparamos los resultados del método riguroso con los valores de los métodos abreviados. El método riguroso se basó en una ecuación de estado como la de Soave-Redlich-Kwong (SRK) para calcular las entalpías y entropías necesarias. Las entalpías y entropías se utilizan para determinar la potencia necesaria y las temperaturas de descarga. Los resultados indicaron que la precisión del método abreviado es sensible al valor de la relación de la capacidad calorífica del estado de gas ideal, k.

Desde el punto de vista del cálculo solamente, el cálculo de la potencia es particularmente sensible a la especificación del caudal másico, la temperatura y la presión de aspiración, y la temperatura y la presión de descarga. Un compresor va a funcionar bajo diferentes valores de las variables que afectan a su rendimiento. Por lo tanto, la parte más difícil del cálculo de un compresor es la especificación de un rango razonable para cada variable y no el cálculo en sí mismo. La referencia enfatiza que el uso de un solo valor para cada variable no es la forma correcta de evaluar un sistema de compresión.

Normalmente, los cálculos termodinámicos se realizan para un proceso ideal (reversible). Los resultados de un proceso reversible se adaptan entonces al mundo real mediante el uso de una eficiencia termodinámica. En el proceso de compresión hay tres procesos ideales que se pueden visualizar 1) un proceso isotérmico (PV1=C1), 2) un proceso isentrópico (PVk=C2) y 3) un proceso politrópico (PVn=C3). Cualquiera de estos procesos puede utilizarse adecuadamente como base para evaluar las necesidades de potencia de compresión mediante cálculos manuales o informáticos. El proceso isotérmico, sin embargo, rara vez se utiliza como base porque el proceso de compresión industrial normal no se lleva a cabo ni siquiera de forma aproximada a temperatura constante.

Nótese que Dresser Rand está realizando bastante trabajo con la compresión a «temperatura casi constante», especialmente para la compresión de CO2 desde chimeneas de ventilación. Para más detalles, consulte:

En este PDM, demostraremos cómo determinar la eficiencia de un compresor a partir de las mediciones de caudal, composición, temperaturas y presiones de aspiración y descarga. Se considera un cálculo riguroso basado en una ecuación de estado y un método abreviado y se comparan los resultados.

Eficiencia del compresor

Las eficiencias del compresor varían con el tipo de compresor, el tamaño y el rendimiento. Sólo pueden determinarse (a posteriori) mediante una prueba del compresor, aunque los fabricantes de compresores suelen proporcionar buenas estimaciones. A efectos de planificación, la referencia sugiere los siguientes valores para las efficiencias globales:

Tabla 1. Eficiencias globales de los compresores

La referencia indica que estas eficiencias globales incluyen la fricción del gas dentro del compresor, las pérdidas mecánicas (rodamientos, juntas, caja de cambios, etc.) y las pérdidas de la caja de cambios. La eficiencia mecánica varía según el tamaño y el tipo de compresor, pero el 95% es un número útil para la planificación. Al calcular el cabezal del compresor y la temperatura de descarga, la efficiencia utilizada será isentrópica o politrópica (la efficiencia isentrópica se denomina a veces efficiencia adiabática). Si se añade un 3-4 % de efficiencia (pérdidas mecánicas) a las efi cencias globales de la tabla 1, se obtendrá generalmente una buena estimación de la efi ciencia termodinámica.

Para evaluar el rendimiento de un compresor existente, el objetivo es calcular la efi ciencia del compresor (η) y la potencia necesaria.

Las propiedades conocidas y medidas son:

a. Caudal volumétrico del gas en condiciones estándar (qS) o caudal másico del gas ()

b. Composición del gas (zi)

c. Presión de aspiración (P1) y temperatura (T1)

d. Presión de descarga (P2) y temperatura (T2)

Estimación de la eficiencia – Método riguroso

El corazón de cualquier software comercial de simulación de flujo de procesos es una ecuación de estado. Debido a su simplicidad y relativa precisión, se utiliza una EOS cúbica como la de Soave Redlich-Kwong (SRK) o la de Peng-Robinson. Estas ecuaciones se utilizan para calcular el equilibrio vapor-líquido (VLE), la entalpía (h) y la entropía (s). Con los coeficientes de interacción binaria adecuados, los resultados de la simulación del proceso de estas dos ecuaciones son prácticamente los mismos. Por lo tanto, en este trabajo sólo se utiliza la SRK.

La eficiencia isentrópica se define por

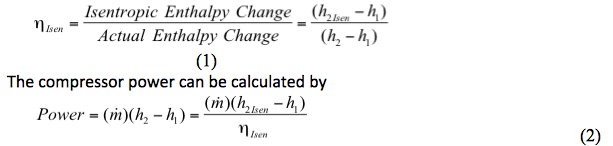
Donde:

ηIsen = Eficiencia isentrópica

h1 = Entalpía de aspiración calculada en P1, T1, y composición (zi)

h2 = Entalpía de descarga calculada en P2, T2, y composición (zi)

h2Isen = Entalpía de descarga isentrópica en P2 (o T2), S2Isen =S1, y composición (zi)

= Caudal másico

El cálculo de la eficiencia o potencia del compresor implica dos pasos

1. Determinación del cambio de entalpía ideal o isentrópico (reversible y adiabático) del proceso de compresión (h2Isen-h1).

2. Determinación del cambio de entalpía real (h2-h1).

El cálculo paso a paso basado en un EOS:

a. Asumir el estado estacionario, es decir,

b. Suponer que la composición de la alimentación no cambia

c. Calcular la entalpía de aspiración h1=f(P1, T1 y zi) y la entropía s1=f(P1, T1 y zi) por EOS

d. Suponga un proceso isentrópico y establezca s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).

e. Calcule la entalpía ideal (h2Isen) en condiciones de descarga para zi, T2 (o P2) y s2Isen conocidos.

f. Calcular la entalpía real (h2) en condiciones de descarga para zi, T2 y P2 conocidos.

g. Calcular el rendimiento isentrópico mediante la ecuación 1: µIsen = (h2Isen – h1)/(h2 – h1)

h. Calcular la potencia por la Ecuación 2:

Estimar la eficiencia – Método abreviado

El exponente de la trayectoria isentrópica (k) o la relación de capacidad calorífica del gas ideal (k=CP/CV) puede calcularse mediante la correlación presentada en el PDM de mayo de 2013:

Donde:

T = Temperatura, K (°R)

= Densidad relativa del gas; relación entre el peso molecular del gas y el peso molecular del aire

A = 0.000272 (0.000151)

La temperatura real de descarga basada en una trayectoria isentrópica puede estimarse mediante

Resolviendo la eficiencia isentrópica,

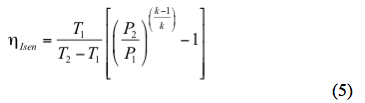
Similarmente, la temperatura real de descarga basada en una trayectoria politrópica puede estimarse (ηPoly) mediante:

La cabeza isentrópica se calcula mediante

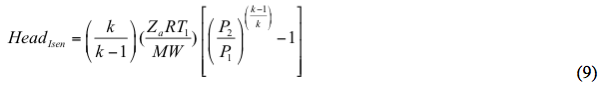
Similarmente, la cabeza politrópica se calcula por

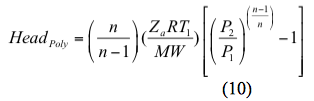
Para un proceso isentrópico (reversible y adiabático) la potencia se calcula por

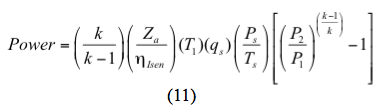
O para un proceso politrópico la potencia se calcula por

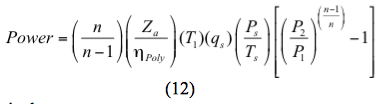
Alternativamente:

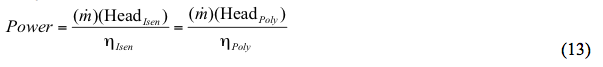
Donde:

Cabeza = Cabeza del compresor, m (pies)

Potencia = Potencia del compresor, kW (HP)

R = Constante universal del gas, 848 kg-m/(kmol-K) o (1545 ft-lbf/(lbmol-°R))

PS = Presión en condiciones estándar, kPa (psia)

P1 = Presión de aspiración, kPa (psia)

P2 = Presión de descarga, kPa (psia)

TS = Temperatura de condición estándar, K (°R)

T1 = Temperatura de aspiración, K (°R)

T2 = Temperatura de descarga, K (°R)

qS = Tasa volumétrica del gas en la condición estándar, Sm3/d (scf/día)

Za = Factor de compresibilidad media del gas = (Z1+Z2)/2

Z1 = Factor de compresibilidad del gas en la condición de aspiración

Z2 = Factor de compresibilidad del gas en la condición de descarga

MW = Peso molecular del gas

El cálculo de la potencia debe hacerse por etapa de compresión y luego sumarse para todas las etapas conectadas a un único conductor.

El cálculo paso a paso para el método abreviado

a. Calcular el exponente isentrópico (k) mediante la ecuación 3 utilizando la temperatura media definida por T = (T1+3T2)/4. Esta forma de temperatura media se definió para obtener una mejor coincidencia entre los resultados del método riguroso y del método abreviado.

b. Calcular la eficiencia isentrópica (ηIsen) mediante la ecuación 5.

c. Calcular el coeficiente politrópico (n) mediante la ecuación 7.

d. Calcular la eficiencia politrópica (ηPoly) mediante la ecuación 8.

e. Calcular los cabezales isentrópico y politrópico mediante las ecuaciones 9 y 10, respectivamente.

f. Calcule la potencia requerida por etapa mediante las ecuaciones 11 o 12.

Estudio de caso

Una mezcla de gas natural se comprime utilizando un compresor centrífugo de tres etapas. El diagrama de flujo del proceso se muestra en la figura 1. Para cada etapa, la presión y la temperatura medidas se presentan en la Tabla 1. La composición de la alimentación medida, los caudales y el peso molecular y la densidad relativa calculados se presentan en la Tabla 2.

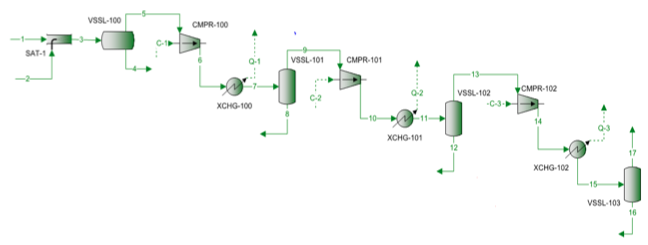
Figura 1. Diagrama de flujo del proceso para una compresión de 3 etapas

Tabla 1. Temperatura y presión medidas para las tres etapas de compresión

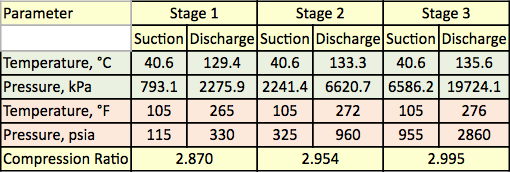
Tabla 2. Análisis y caudal de gas para las tres etapas de compresión

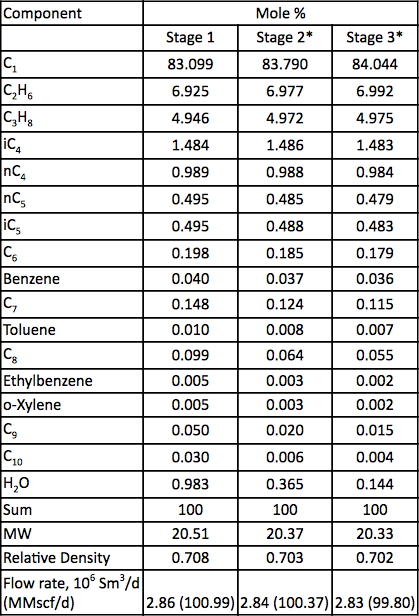
* Calculado

Resultados y discusiones

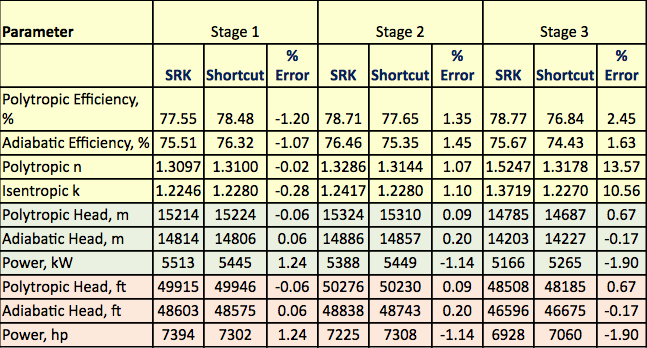
El diagrama de flujo del proceso mostrado en la Figura 1 fue simulado por el software ProMax para realizar los cálculos rigurosos utilizando el EOS de SRK. El programa calculó las eficiencias politrópica e isentrópica, los cabezales y la potencia de compresión. El programa también calculó el exponente de la trayectoria isentrópica (k), y el exponente de la trayectoria politrópica (n). Estos resultados calculados se presentan en la Tabla 2 para las tres etapas bajo rúbricas SRK. Los cálculos realizados por ProMax son muy similares al paso a paso de a a h descrito en la sección rigurosa. En la Tabla 2 también se presentan los resultados de los cálculos abreviados para los valores correspondientes en el epígrafe abreviado. Los cálculos abreviados se basan en el paso a paso de a a f descrito en la sección del método abreviado. El porcentaje de error entre el método riguroso y los métodos abreviados para cada etapa se presenta también en la Tabla 2. La Tabla 2 indica que se obtienen excelentes acuerdos para las etapas 1 y 2. Sin embargo, se observan mayores desviaciones para los exponentes isotrópico y politrópico de la etapa 3 debido a la operación a alta presión que se desvía demasiado de las condiciones del estado de gas ideal.

Tabla 3. Resumen de los resultados calculados de forma rigurosa y abreviada

Conclusiones

La tabla 2 indica que hay buenos acuerdos entre los resultados abreviados y los rigurosos. Las diferencias entre los resultados del método riguroso y del método abreviado para los cálculos de las instalaciones y la planificación son insignificantes. Para la etapa 3, debido a la operación a alta presión y a la desviación de la condición de estado de gas ideal, se observa un error mayor para el exponente isentrópico (k).

El exponente isentrópico calculado (k) en el ProMax no es la relación de capacidad calorífica del estado de gas ideal (CP/CV). Es el valor del exponente isentrópico que se requiere para producir una trayectoria isentrópica desde la entrada hasta la salida. Su valor se calcula como una integración de esa trayectoria. Por lo tanto, es un valor «medio» que representa la verdadera trayectoria isentrópica. Para los gases ideales, el valor sería igual a la relación (CP/CV).

Este error en ‘k’ también ilustra la importancia de especificar qué correlación se va a utilizar cuando se pida una prueba de rendimiento (es decir, consulte ASME PTC-10 para obtener detalles adicionales), de modo que el cliente y el proveedor estén de acuerdo en avanzar con respecto al peso molecular (MW) y k para el fluido de prueba. Para más detalles, consulte la referencia y los PDM de agosto y septiembre de 2010.

También puede valer la pena señalar que cuando se hace la tendencia de ‘n’ y la eficiencia politrópica para evaluar la condición de la máquina, la precisión relativa de los instrumentos/equipos de medición (transductores de temperatura y presión) y el mapeo del rendimiento del compresor a la curva de rendimiento original (tasa de flujo de volumen de gas real frente a la velocidad), introduce muchas fuentes erróneas potenciales en esta evaluación diaria.

Nótese que la precisión de los métodos abreviados depende de los valores de k y n. La definición de la temperatura media en el método abreviado se ajustó para obtener una mejor coincidencia entre el exponente de la trayectoria isentrópica (k) calculado por el método riguroso.

Para aprender más sobre casos similares y cómo minimizar los problemas operativos, le sugerimos que asista a nuestros cursos G4 (Acondicionamiento y Procesamiento de Gas), PF4 (Instalaciones de Producción y Procesamiento de Petróleo), ME46 (Sistemas de Compresores-Diseño Mecánico y Especificaciones) y ME44 (Fundamentos de Sistemas de Bombas y Compresores).

PetroSkills ofrece servicios de consultoría sobre este tema y muchos otros. Para más información sobre estos servicios, visite nuestra página web en http://petroskills.com/consulting, o envíenos un correo electrónico a [email protected].

Dr. Mahmood Moshfeghian

Referencia:

3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.

4. Peng, D. Y., y Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.

5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.

6. ASME PTC-10, «Performance test Code on Compressors and Exhausters», 1997.

7. Honeywell, J. «Important Aspects of Centrifugal Compressor Testing-Part 1», Consejo del mes, agosto de 2010

8. Honeywell, J. «Important Aspects of Centrifugal Compressor Testing-Part 2», Consejo del mes, septiembre de 2010