Galileo es a menudo considerado el padre de la ciencia moderna. Fue él quien reunió los principios del experimento, la teoría y las matemáticas en un marco estándar. Probablemente, más que nadie, Galileo fue la persona responsable del desarrollo de la ciencia moderna.
Se dice que Galileo dejó caer dos bolas de acero de diferentes masas, pero del mismo material desde la torre inclinada de Pisa y aterrizaron al mismo tiempo. Lo notable de este experimento es que introdujo un nuevo método de hacer ciencia en el que se realiza un experimento para comprobar una hipótesis. Demostró que no basta con pensar que algo es cierto, sino que hay que demostrarlo.

Galileo encontró una interesante paradoja mientras dirigía el Departamento de Matemáticas de la Universidad de Pisa.
Definición: Una paradoja, también conocida como antinomia, es un enunciado lógicamente autocontradictorio o un enunciado que va en contra de lo que uno espera. (Wikipedia). (Griego: «para» = más allá, «doxa» = creencia)
La paradoja de Galileo trataba de determinar si dos conjuntos que contienen infinitos objetos son equivalentes entre sí. Por ejemplo, sea P el conjunto de enteros positivos donde P= {0,1,2,3,…} y E el conjunto de números pares donde E = {0,2,4,6,…}. Galileo afirmó que los tamaños de estos dos conjuntos van a ser los mismos porque podemos emparejar cada uno de los enteros positivos del conjunto P con los números pares del conjunto E.

Entonces, ¿cómo es que el tamaño de los dos conjuntos es el mismo cuando aparece un número «menos» en E? Esto se llamó la paradoja de Galileo e inició un nuevo debate sobre el concepto de infinito.
Después de Galileo, su alumno Evangelista Torricelli se convirtió en el jefe del Departamento de Matemáticas de la Universidad de Pisa. Es posible que le hayas oído hablar por sus trabajos sobre la presión atmosférica y la invención del barómetro. Como Toricelli también se interesa por las matemáticas, se pregunta:
¿Es posible tener un objeto con un volumen finito y una superficie infinita? En primer lugar, tal cosa parece improbable para la mayoría de nosotros. Sin embargo, las matemáticas nos dicen que tal cosa podría ocurrir. Torricelli respondió a su pregunta y descubrió la Trompeta de Toricelli, cuya superficie es infinita, pero cuyo volumen es finito. Su descubrimiento visto como una paradoja «increíble».
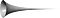
Por cierto, hay una regla esencial en la filosofía de las matemáticas; Sea cual sea la época de la filosofía o de las matemáticas que se trate, está relacionada con la historia, la cultura y la religión de esa región. Por eso llaman a la trompeta de Toricelli también el cuerno de Gabriel. Aquí se hace una referencia a la Biblia porque los cristianos creen que el ángel, Gabriel, tocará el cuerno en el Día del Juicio Final.
¿Entonces cómo se forma la trompeta de Toricelli? Todos sabemos cómo graficar y=x. Si en cambio graficamos la ecuación y=1/x donde x es mayor o igual a 1, la gráfica será así:
Cuando tomamos la gráfica de y=1/x y la giramos alrededor del eje x, vemos la trompeta de Toricelli.

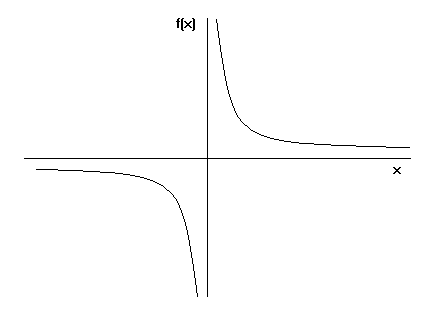
Afortunadamente, tenemos en nuestras manos fórmulas matemáticas para calcular el área y el volumen de la trompeta de Toricelli. Cuando utilizamos la fórmula de integración siguiente para el volumen de la trompeta, obtenemos una cantidad finita.
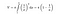
Sin embargo, cuando aplicamos la fórmula de integración para la superficie de la trompeta, esta vez, la superficie de la misma se convierte en infinita. ¿No es interesante este resultado?
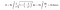
Como el volumen de la trompeta de Toricelli es finito, podemos llenarla con una cantidad finita de pintura. Por ejemplo, supongamos que su volumen es de 100 litros. Voy a Home Depot y compro 100 litros de pintura y la lleno. Sin embargo, lo que hace esto interesante es que habré pintado la superficie infinita con esos 100 litros de pintura. Hoy en día, la mayoría de la gente llama a esta paradoja, «la paradoja del pintor».
¡Houston, tenemos un problema aquí! La situación que es imposible en la práctica se hace posible en las matemáticas. Entonces, ¿cómo puede ser real la trompeta de Torricelli? O, ¿cómo podemos hacer coincidir con precisión todos los elementos de los conjuntos mientras uno de los conjuntos es un subconjunto de otro en el ejemplo de Galileo?
La razón de todos estos conflictos es que el concepto de infinito no es similar a otros conceptos que conocemos, y eso confunde a mucha gente. Galileo dice para su paradoja,
«Sí, amigo mío, existe el infinito. Es inútil objetarlo. Los conjuntos en los que estoy trabajando son ejemplos de conjuntos cerrados que implican el infinito. Empiezan en un punto y siguen hasta el infinito, y sin embargo, siguen siendo conjuntos. Sin embargo, mis comentarios y conceptos sobre el infinito deben ser diferentes de los que utilizaría para las magnitudes finitas. Si se trata de magnitudes finitas, se puede decir que 3 kilos son menos que 5 kilos, o que 32 metros son más largos que 7 metros. Pero cuando se trata del infinito, no se puede decir que este infinito es más grande, más pequeño o igual que aquél.»
Esa fue la solución de Galileo 1600s.
Desgraciadamente, la solución de Galileo había iniciado un nuevo debate sobre el infinito. Los matemáticos y los filósofos no pudieron ponerse de acuerdo en una respuesta específica hasta que Cantor compartió su «teoría de conjuntos», que los estudiantes aprenden en la escuela primaria hoy en día.
Podemos historiar periódicamente el desarrollo de la idea de infinito. Surgió por primera vez de los Eleáticos, que fue una escuela de filosofía presocrática fundada por Parménides a principios del siglo V a.C. en la antigua ciudad de Elea. Hubo tres grandes filósofos en esta escuela, como Zenón, Jenófanes y Parménides. En esta escuela, la filosofía aceptada era que la existencia era singular, y no había pluralidad. Zenón fue famoso por sus paradojas sobre el infinito en los Eleáticos. Más tarde, en los años 300 a.C., Aristóteles surgió y propuso un par de conceptos para explicar las paradojas de Zenón, que eran el infinito potencial y el infinito real.
El infinito potencial es un grupo de números o grupo de «cosas» que continúa sin terminar, continuando o repitiéndose una y otra vez sin punto final reconocible.
El infinito real implica conjuntos o «cosas» interminables dentro de un espacio que tiene un principio y un final; es una serie que está técnicamente «completada» pero que consta de un número infinito de miembros.
Aristóteles creía que no existía el infinito real. Esta idea de Aristóteles dominó el mundo de la filosofía hasta los años 1600. Entonces filósofos como Cusa y Bruno afirmaron que existe el infinito real, pero que no podemos darle sentido. Después de Cuso y Bruno, el gran pensador Spinoza se unió al tema.
Spinoza dijo que podíamos entender el concepto de infinito y clasificarlos en tamaño. Sin embargo, también afirmó que no podía hacer las cuentas de ellos. Por ejemplo, podía sumar 3 a 5, pero no podía sumar un infinito a otro.
Finalmente, para terminar esos debates, apareció un hombre hermoso, Georg Cantor, que encontró la teoría de conjuntos, que sigue siendo la base de las matemáticas. Él puso el punto final a las discusiones sobre el infinito con su teoría de conjuntos.
Nos demostró que un conjunto infinito sería mayor o menor que otro conjunto infinito. Además, Cantor afirmó que podíamos sumar y multiplicar conjuntos infinitos. Hasta ese momento, los humanos habían seguido las ideas de Aristóteles sobre el infinito. Según Aristóteles, si multiplicamos el número 3 por el infinito, volvería a ser infinito. El infinito lo engulliría todo. Basándose en esto, afirmó que sólo habría infinito potencial, no infinito real.
Sin embargo, Cantor nos demostró lo contrario de la idea de Aristóteles con la teoría de conjuntos. Si añadimos uno a un conjunto infinito, ya no será el mismo conjunto. Intentó comparar los infinitos. Por ejemplo, Cantor demostró que el conjunto de todas las funciones de (0,1)→ℕ es contable. Así, definió una función unívoca y onto del intervalo (0,1) a los números naturales.
En otras palabras, demostró que todos los números naturales pueden caber entre el 0 y el 1 porque había infinitos números racionales entre el 0 y el 1, y estos infinitos se pueden emparejar. Luego hizo algo aún más peligroso que encontrar dos infinitos iguales. Comparó la infinidad de números reales con la infinidad de números naturales y encontró que la infinidad de números reales es mayor que la otra. Incluso miró su prueba y le dijo a su amigo Dedekind: «Lo veo, pero ni siquiera yo puedo creerlo…».
Cantor era también un matemático con preocupaciones filosóficas y religiosas muy serias. Mientras desarrollaba la teoría de conjuntos, dijo: «Dios me dictó la teoría de conjuntos».
La teoría de conjuntos no era muy aceptada cuando se desarrolló por primera vez. Las empresas ni siquiera contrataban a Cantor para ningún trabajo. Un matemático, Henri Poincaré, dijo una vez: «Las ideas de este Cantor son una mala enfermedad que se pega al cuello de las matemáticas. Y las matemáticas lo tratarán algún día». Cantor tuvo que ingresar en un hospital psiquiátrico durante un tiempo y allí murió. Pero hoy lo consideramos un genio.
Cantor era un hombre solitario al borde del infinito. Citó la Biblia al principio de su artículo sobre los números transfinitos: «Todo lo que está oculto saldrá a la luz».