Imagina un cuadrado de papel que yace plano en tu escritorio. Te pido que cierres los ojos. Oyes cómo se desplaza el papel. Cuando abres los ojos, el papel no parece haber cambiado. ¿Qué podría haber hecho mientras no estabas mirando?
Es obvio que no he girado el papel 30 grados, porque entonces el papel tendría un aspecto diferente.

Tampoco le he dado la vuelta a través de una línea que conectara, por ejemplo, una de las esquinas con el punto medio de otro borde. El papel tendría un aspecto diferente si lo hubiera hecho.

Lo que sí podría haber hecho es girar el papel en el sentido de las agujas del reloj o en sentido contrario en cualquier múltiplo de 90 grados, o voltearlo a través de cualquiera de las líneas diagonales o de las líneas horizontales y verticales.
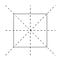
Una forma útil de visualizar las transformaciones es marcar las esquinas del cuadrado.

La última opción es la de no hacer nada. Esto se llama la transformación de identidad. En conjunto, todas estas se llaman las transformaciones de simetría del cuadrado.
Puedo combinar las transformaciones de simetría para hacer otras transformaciones de simetría. Por ejemplo, dos vueltas sobre el segmento de línea BD producen la identidad, al igual que cuatro rotaciones sucesivas de 90 grados en sentido contrario a las agujas del reloj. Un giro sobre la línea vertical seguido de un giro sobre la línea horizontal tiene el efecto seguro de una rotación de 180 grados. En general, cualquier combinación de transformaciones de simetría producirá una transformación de simetría. La siguiente tabla da las reglas para componer transformaciones de simetría:

En esta tabla, R con los subíndices 90, 180 y 270 denotan rotaciones en sentido contrario a las agujas del reloj de 90, 180 y 270 grados, H significa una vuelta sobre la línea horizontal, V es una vuelta sobre la línea vertical, MD es una vuelta sobre la diagonal de arriba a la izquierda y OD significa una vuelta sobre la otra diagonal. Para encontrar el producto de A y B, ve a la fila de A y luego a la columna de B. Por ejemplo, H∘MD=R₉₀.
Hay algunas cosas que puedes notar mirando la tabla:
- La operación ∘ es asociativa, lo que significa que A∘(B∘C) = (A∘B)∘C para cualquier transformación A, B y C.
- Para cualquier par de transformaciones de simetría A y B, la composición A∘B es también una transformación de simetría
- Hay un elemento e tal que A∘e=e∘A para toda A
- Para toda transformación de simetría A, existe una única transformación de simetría A-¹ tal que A∘A-¹=A-¹∘A=e
Por tanto, decimos que la colección de transformaciones de simetría de un cuadrado, combinada con la composición, forma una estructura matemática llamada grupo. Este grupo se llama D₄, el grupo diedro del cuadrado. Estas estructuras son el objeto de este artículo.
Definición de un grupo
Un grupo ⟨G,*⟩ es un conjunto G con una regla * para combinar dos elementos cualesquiera en G que satisface los axiomas de grupo:
En el resumen solemos suprimir * y escribir a*b como ab y referirnos a * como multiplicación.

No es necesario que * sea conmutativo, es decir, que a*b=b*a. Se puede ver esto mirando la tabla de D₄, donde H∘MD=R₉₀ pero MD∘H=R₂₇₀. Los grupos en los que * es conmutativo se llaman grupos abelianos en honor a Neils Abel.
Los grupos abelianos son la excepción más que la regla. Otro ejemplo de grupo no abeliano son las transformaciones de simetría de un cubo. Consideremos sólo las rotaciones alrededor de los ejes:
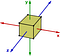
Si primero giro 90 grados en sentido contrario a las agujas del reloj sobre el eje y y luego 90 grados en sentido contrario a las agujas del reloj sobre el eje z entonces el suyo tendrá un resultado diferente que si girara 90 grados sobre el eje z y luego 90 grados sobre el eje y.

Es posible que un elemento sea su propio inverso. Consideremos el grupo formado por 0 y 1 con la operación de adición binaria. Su tabla es:

Claramente el 1 es su propio inverso. Esto también es un grupo abeliano. No te preocupes, la mayoría de los grupos no son tan aburridos.
Algunos ejemplos más de grupos incluyen:
- El conjunto de los números enteros con adición.
- El conjunto de los números racionales que no incluyen el 0 con multiplicación.
- El conjunto de las soluciones de la ecuación polinómica xⁿ-1=0, llamadas las nth raíces de la unidad, con multiplicación.
Aquí tienes algunos ejemplos que no son grupos:
- El conjunto de los números naturales bajo adición no es un grupo porque no hay inversos, que serían los números negativos.
- El conjunto de todos los números racionales incluyendo el 0 con la multiplicación no es un grupo porque no hay ningún número racional q para el que 0/q=1, por lo que no todo elemento tiene un inverso.
Estructura de grupo
Un grupo es mucho más que una mancha que satisface los cuatro axiomas. Un grupo puede tener estructura interna, y esta estructura puede ser muy intrincada. Uno de los problemas básicos del álgebra abstracta es determinar cómo es la estructura interna de un grupo, ya que en el mundo real los grupos que se estudian realmente son mucho más grandes y complicados que los simples ejemplos que hemos dado aquí.
Uno de los tipos básicos de estructura interna es un subgrupo. Un grupo G tiene un subgrupo H cuando H es un subconjunto de G y:
- Para a,b∈H, a*b∈H y b*a∈H
- Para a∈H, a-¹∈H
- La identidad es un elemento de H
Si H≠G entonces se dice que H es un subgrupo propio. El subgrupo de G formado sólo por la identidad se llama subgrupo trivial.
Un grupo no abeliano puede tener subgrupos conmutativos. Consideremos el grupo diédrico cuadrado del que hablamos en la introducción. Este grupo no es abeliano pero el subgrupo de rotaciones es abeliano y cíclico:
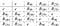
Damos ahora dos ejemplos de estructura de grupos.
Incluso si un grupo G no es abeliano, puede darse el caso de que exista una colección de elementos de G que conmuten con todo lo que hay en G. Esta colección se llama centro de G. El centro C es un subgrupo de G. Prueba:
Supongamos ahora que f es una función cuyo dominio y rango son ambos G. Un período de f es un elemento a∈G tal que f(x)=f(ax) para todo x∈G. El conjunto P de períodos de f es un subgrupo de G. Prueba:
Los grupos finitos son generados finitamente
Vimos que los grupos cíclicos están generados por un solo elemento. Cuando es posible escribir cada elemento de un grupo G como productos de un subconjunto (no necesariamente propio) A de G entonces decimos que A genera G y escribimos esto como G=⟨A⟩. La prueba más «bueno, duh» que jamás verás es la prueba de que todos los grupos finitos son generados por un conjunto generador finito:
- Sea G finito. Cada elemento de G es un producto de otros dos elementos de G por lo que G=⟨G⟩. QED.

Terminaremos este artículo con una aplicación.
Comunicación resistente a errores
La forma más sencilla de transmitir información digital es codificarla en cadenas binarias de longitud fija. Ningún esquema de comunicación está completamente libre de interferencias, por lo que siempre existe la posibilidad de que se reciban datos erróneos. El método de decodificación de máxima probabilidad es un enfoque simple y eficaz para detectar y corregir los errores de transmisión.
Sea 𝔹ⁿ el conjunto de cadenas binarias, o palabras, de longitud n. Es sencillo demostrar que 𝔹ⁿ es un grupo abeliano bajo adición binaria sin acarreo (de modo que, por ejemplo, 010+011=001). Nótese que cada elemento es su propio inverso. Un código C es un subconjunto de 𝔹ⁿ. El siguiente es un ejemplo de un código en 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Los elementos de un código se llaman codewords. Sólo se transmiten las palabras clave. Se dice que hay un error cuando una interferencia cambia un bit de una palabra transmitida. La distancia d(a,b) entre dos palabras clave a y b es el número de dígitos en los que difieren dos palabras clave. La distancia mínima de un código es la menor distancia entre dos codificadores cualesquiera. Para el ejemplo de código anterior, la distancia mínima es tres.
En el método de decodificación de máxima probabilidad, si recibimos una palabra x, que puede contener errores, el receptor debe interpretar x como la palabra clave a tal que d(a,x) sea un mínimo. Demostraré que para un código de distancia mínima m esto siempre puede (1) detectar errores que cambian menos de m bits y (2) corregir errores que cambian ½(m-1) o menos bits.

En nuestro código de ejemplo, m=3 y la esfera de radio ½(m-1)=1 sobre la palabra clave 011101 es {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Así que si el receptor recibe cualquiera de estas palabras, sabe que debía recibir 011101.
Así que todo eso está muy bien, pero ¿qué tiene que ver todo esto con la teoría de grupos? La respuesta está en cómo producimos realmente los códigos con los que trabaja este método.
Es posible que un código en 𝔹ⁿ forme un subgrupo. En este caso decimos que el código es un código de grupo. Los códigos de grupo son grupos finitos, por lo que se generan de forma finita. Veremos cómo producir un código encontrando un grupo generador.
Un código se puede especificar de forma que los primeros bits de cada palabra de código se llamen bits de información y los bits del final se llamen bits de paridad. En nuestro código de ejemplo C, los tres primeros bits son de información y los tres últimos de paridad. Los bits de paridad satisfacen las ecuaciones de comprobación de paridad. Para un código A₁A₂A₃A₄A₅A₆ las ecuaciones de paridad son A₄=A₁+A₂, A₅=A₂+A₃ y A₆=A₁+A₃. Las ecuaciones de paridad proporcionan otra capa de protección contra los errores: si alguna de las ecuaciones de paridad no se satisface, entonces se ha producido un error.
Esto es lo que hacemos. Supongamos que queremos acordes de código con m bits de información y n bits de paridad. Para generar un código de grupo, escribe una matriz con m filas y m+n columnas. En el bloque formado por las primeras m columnas, escribe la matriz m×m de identidad. En la columna j de m+1≤j≤m_n, escriba un 1 en la kª fila si Aₖ aparece en la ecuación de paridad para el bit de paridad Aⱼ y 0 en caso contrario. En nuestro código de ejemplo, la matriz es:

Tal matriz se llama matriz generadora del código de grupo. Se puede comprobar directamente que las filas generan C:

Las filas de cualquier matriz generadora forman un conjunto generador para un código de grupo C. Prueba:
- Identidad e inversos: Cualquier fila sumada a sí misma da la identidad, una cadena formada por todos los ceros.
- Cierre: Si A,B∈C entonces A y B son sumas de filas de la matriz generadora por lo que A+B es también una suma de filas de la matriz generadora. Por lo tanto A+B∈C.
Esto nos permite generar un código, ahora mostraré cómo generar un código útil.
Define el peso w(x) para significar el número de unos en x. Por ejemplo, w(100101)=3. Es obvio que w(x)=d(x,0) donde 0 es una palabra cuyos dígitos son todos ceros. El peso mínimo W de un código es el peso de la palabra clave no nula con menos unos en el código. Para un código de distancia mínima m, d(x,0)≥m por lo que w(x)≥m y, por lo tanto, W=m.
Recordemos que para que una palabra se considere una palabra clave, debe satisfacer un conjunto de ecuaciones de comprobación de paridad. Para nuestro código de ejemplo, éstas son A₄=A₁+A₂, A₅=A₂+A₃, y A₆=A₁+A₃. También podemos escribirlos como un sistema lineal:
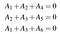
Que a su vez puede escribirse en términos de productos punto:

O en forma más compacta como Ha=0 donde a=(A₁,A₂,A₃,A₄,A₅,A₆) y H es la matriz de comprobación de paridad del código:

Se puede comprobar por cálculo directo que si w(a)≤2 entonces no podemos tener Ha=0. En general, el peso mínimo es t+1 donde t es el menor número tal que cualquier colección de t columnas de H no suman cero (es decir, son linealmente independientes). Demostrar esto nos llevaría demasiado lejos en el álgebra lineal.
Si eso te asusta, no te preocupes. Podemos producir algunos códigos muy buenos sin ello aprovechando el hecho de que el resultado que acabo de mencionar implica que si cada columna de H es distinta de cero y no hay dos columnas iguales, entonces el peso mínimo, y por tanto la distancia mínima del código, es al menos tres. Esto es muy bueno: si se espera que nuestro sistema de comunicación tenga un error de bit por cada cien palabras transmitidas, entonces sólo una de cada diez mil palabras transmitidas tendrá un error no corregido y una de cada millón de palabras transmitidas tendrá un error no detectado.
Así que ahora tenemos una receta para producir un código útil para el esquema de detección de máxima probabilidad para las palabras de código que contienen m bits de información y n bits de paridad:
- Crear una matriz con m+n columnas y n filas. Rellenar la matriz con unos y ceros de forma que no haya dos columnas iguales y ninguna columna sea sólo ceros.
- Cada fila de la matriz de comprobación de paridad resultante corresponde a una de las ecuaciones de bits de paridad. Escríbalos como un sistema de ecuaciones y resuelva de manera que cada bit de paridad se escriba en términos de los bits de información.
- Cree una matriz con m+n columnas y m filas. En el bloque formado por las primeras m columnas, escribe la matriz identidad m×m. En la columna j de m+1≤j≤m_n, escribe un 1 en la kª fila si Aₖ aparece en la ecuación de paridad para el bit de paridad Aⱼ y 0 en caso contrario.
- Las filas de esta matriz son los generadores de un grupo de códigos con distancia mínima de al menos tres. Este es el código que utilizaremos.
Como ejemplo, supongamos que necesito un código sencillo de ocho palabras y que sólo necesito algo de detección básica de errores y no de corrección, por lo que puedo salir del paso con una distancia mínima de dos. Quiero tres bits de información y dos de paridad. Escribo la siguiente matriz de comprobación de paridad:
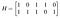
Hay dos pares de columnas que son iguales, así que la t más pequeña para la que cualquier colección de t columnas es linealmente independiente es uno, por lo que el peso mínimo, y por tanto la distancia mínima que tendré, es dos. Las filas representan las ecuaciones de comprobación de paridad A₄=A₁+A₃ y A₅=A₁+A₂+A₃. Mi matriz generadora es por tanto:

Y las filas de esta matriz generan el grupo de códigos:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Observaciones finales
El álgebra abstracta es un tema profundo con implicaciones de gran alcance, pero también es muy fácil de aprender. Aparte de algunas menciones de pasada al álgebra lineal, casi todo lo que he tratado aquí es accesible para alguien que sólo haya cursado álgebra en la escuela secundaria.
Cuando se me ocurrió escribir este artículo, realmente quería hablar del cubo de Rubik, pero al final quise elegir un ejemplo que pudiera cubrirse sólo con las ideas más básicas de la teoría de grupos. Además, hay tanto que decir sobre el grupo del cubo de Rubik que se merece un artículo independiente, así que éste llegará pronto.
Mis cursos universitarios de álgebra abstracta se basaron en el libro A Book of Abstract Algebra de Charles Pinter, que es un tratamiento accesible. Los ejemplos de este artículo se han tomado prestados, con algunas modificaciones, de Pinter.
Como nota final, cualquier imagen que no se cite es mi propio trabajo original y puede utilizarse con atribución. Como siempre, agradezco cualquier corrección o solicitud de aclaración.