Lo que sigue es mi opinión sobre algunos problemas matemáticos de supuesta «matemática de núcleo común» o «nueva matemática» que han circulado por internet. Creo que nos muestran una implementación mal orientada de las CCS.

Tenga en cuenta que no todo lo que ve en los libros de matemáticas o en internet está bien hecho en base a las CCS. En algunos de los ejemplos que se ven, parece que la gente está tirando el sentido común al hacer problemas de matemáticas para abordar los estándares del núcleo común.

No me sorprende que la implementación haya terminado siendo «chapucera» en algunos lugares. Los CCS son un cambio tan grande para la mayoría de los profesores que necesitan mucho apoyo y reeducación antes de que se les exija enseñar con ellos.

Siempre he pensado que el PRINCIPAL problema al que se enfrenta la educación matemática en los grados elementales de las escuelas públicas es que muchos profesores de primaria no entienden las matemáticas lo suficiente como para poder enseñarlas bien incluso en el nivel elemental. Por ejemplo, muchos de ellos no entienden los conceptos, los porqués de los algoritmos que enseñan. No es culpa suya, el problema se remonta a lo que se les enseñó en la formación de profesores y en su propia educación.

Incluso el propio documento de las normas es algo difícil de seguir en algunas partes. Su lectura requiere cierta reflexión. Me gustaría que alguien produjera un folleto que explicara los estándares en un lenguaje sencillo y con numerosos ejemplos.

Malos ejemplos de «common core» o «nuevas matemáticas»

Ejemplo 1

Recientemente vi una imagen de estrategias de sustracción en Facebook que decía que era de un libro de matemáticas de 1º de primaria y que era «Common Core math.»

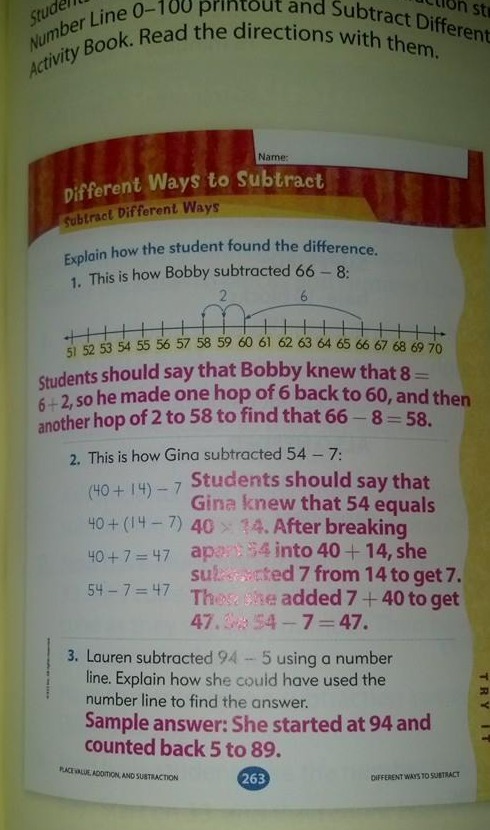
Creo que el método 2 es demasiado difícil para 1º grado, y dejaría incluso el método 1 para 2º grado.

Sin embargo, ese libro no parece siquiera alinearse con los estándares de Common Core. Los estándares para 1er grado simplemente no incluyen ese tipo de problemas de resta.

Esto es lo que encontramos en los estándares:

Sumar y restar dentro de 20.
1.OA.5
Relacionar el conteo con la suma y la resta (por ejemplo, contando con 2 para sumar 2).
1.OA.6.
Añadir y restar dentro de 20, demostrando fluidez para sumar y restar dentro de 10. Utilizar estrategias como contar; hacer diez (p. ej., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); descomponer un número que lleva a una decena (p. ej., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); utilizar la relación entre la adición y la sustracción (p. ej., sabiendo que 8 + 4 = 12, se sabe que 12 – 8= 4); y crear sumas equivalentes pero más fáciles o conocidas (p. ej, sumar 6 +7 creando el equivalente conocido 6 + 6 + 1 = 12 + 1 = 13).

El ejemplo del libro de texto parece querer abordar el 1.OA.6 anterior, pero eso es claramente para sumar y restar dentro de 20, no con números más grandes.

Más adelante en los estándares de 1er grado vemos dos estándares que tienen que ver con restar números de dos dígitos (dentro de 100):

1.NBT.5.
Dado un número de dos cifras, encontrar mentalmente 10 más o 10 menos que el número, sin tener que contar; explicar el razonamiento utilizado.
1.NBT.6.
Resta múltiplos de 10 en el rango 10-90 de múltiplos de 10 en el rango 10-90 (diferencias positivas o nulas), utilizando modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relaciona la estrategia con un método escrito y explica el razonamiento utilizado.
Nota de María: se trata de restas como 34 – 20 u 89 – 60.

Pero ninguna de ellas incluye sustracciones como 54 – 7 o 82 – 6. Esas están en 2º grado:

2.NBT.5
Sumar y restar con fluidez dentro de 100 utilizando estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta.

Nótese que el estándar de 2º grado no especifica CÓMO se resta (si se utilizan estrategias de matemáticas mentales o se escriben los números uno debajo del otro y se toman prestados/se agrupan).

Ejemplo 2

De Houghton Mifflin, supuestamente:

Juanita quiere dar bolsas de cromos a sus amigos. Quiere dar el mismo número de pegatinas a cada amigo. No está segura de si necesita 4 bolsas o 6 bolsas de cromos. ¿Cuántas pegatinas podría comprar para que no le sobren?

El problema de las pegatinas tiene que ver con el concepto de mínimo común múltiplo (MCD). (La respuesta es que debería comprar 12, 24, 36, o cualquier otro múltiplo de 12 pegatinas, porque entonces puede dividirlas en 4 bolsas o en 6 bolsas.)

Claro, el problema es MUY poco claro y está mal redactado. Mi opinión es que el folleto en el que aparece esto está simplemente sin editar. No es culpa de las normas en sí. Estoy de acuerdo con Bart Goddard en el Foro de Matemáticas. Esto es un síntoma de la prisa ciega por producir problemas de la historia «de la vida real» que terminan siendo disparatados.

Desde el documento PDF en el que aparece, concluyo que el problema es para cuarto grado, porque todos los demás problemas de palabras en el folleto coinciden con los estándares para cuarto grado (factores, primos). Pero los CCS ni siquiera incluyen el mínimo común múltiplo en los estándares de 4º grado (¡está en el 6º!). Algo se ha torcido mucho con ese problema de palabras.

Ejemplo 3

De nuevo, supuestamente de Houghton Mifflin para 1º grado. Esto coincide con la norma que ya cité arriba:

Sumar y restar dentro de 20.
1.OA.6.
Añadir y restar dentro de 20, demostrando fluidez para sumar y restar dentro de 10. Utilizar estrategias como contar; hacer diez (p. ej., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); descomponer un número que lleva a una decena (p. ej., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); utilizar la relación entre la suma y la resta (p. ej, sabiendo que 8 + 4 = 12, se sabe que 12 – 8= 4); y creando sumas equivalentes pero más fáciles o conocidas (por ejemplo, sumar 6 +7 creando el equivalente conocido 6 + 6 + 1 = 12 + 1 = 13).

Ahora bien, en primer lugar, la estrategia de «hacer diez» tiene que ver con la ADICIÓN, no con la resta. En la resta, se llama «descomponer un número que lleva a una decena». Así que las instrucciones deberían decir: «¿Qué muestra una forma de descomponer un número que lleva a una decena?». Creo que es una completa tontería exigir a los alumnos de primer grado que conozcan esa terminología.

Pero hay otro problema aquí. Si realmente lee todos los estándares, se dará cuenta de que en otros lugares se pide a los estudiantes que expliquen el razonamiento utilizado o que relacionen un determinado método visual con la estrategia, ¡pero NO en este estándar!

La forma en que veo este estándar es que se supone que los maestros deben ENSEÑAR las diversas trategias mencionadas y luego dar a los estudiantes problemas SIMPLES de suma y resta dentro de 20 como 15 – 8 y 10 – 6. NO veo que este estándar requiera que los estudiantes reconozcan si un determinado modelo visual se corresponde con una determinada estrategia.

De nuevo, parece que el autor tira el sentido común… y no entiende realmente los estándares.

Ejemplo 4

El ejemplo de abajo está muy mal redactado pero el CONCEPTO que hay detrás es muy bueno y también se encuentra en Math Mammoth. Por lo tanto, puedo entender lo que quieren.

Ves cinco cuadrados. Colorea algunos de azul y el resto de rojo. Eso está claro.

Entonces colorea los cuadrados del «bono numérico» de la misma manera. El lazo numérico va a esos tres círculos. Un niño que haya estado presente en una clase en la que el profesor enseñe los bonos numéricos es de esperar que sepa lo que significa. Es el mismo concepto que una familia de hechos… el número de arriba es la suma o el total (5), y los números que van a los círculos de abajo corresponden a cuántos coloreaste de azul y cuántos de rojo, en este caso 1 y 4.

Entonces creo que las parejas ocultas son también el 1 y el 4. Muestra 1 y 4 dedos a un adulto. Por último colorea 1 y 4 dedos en el dibujo (y no tus propios dedos como parece).

En mi opinión la parte de los dedos es superflua y confusa. Sin embargo, el concepto de enlaces numéricos es mucho más antiguo que el CCS. En realidad, los enlaces numéricos no se mencionan en el CCS, aunque sí se relacionan con este estándar:

1.OA.4
Comprender la resta como un problema de suma desconocida. Por ejemplo, restar 10 – 8 encontrando el número que hace 10 cuando se suma a 8.

y con este

1.OA.6.
Añadir y restar dentro de 20, demostrando fluidez para la adición y la sustracción dentro de 10.

No sé por qué esa hoja de trabajo de enlace numérico se da como un ejemplo de Common Core Math. Sería mucho mejor titularla como un ejemplo de hoja de trabajo de matemáticas mal redactada que PODRÍA incluso datar de antes del Common Core (y que simplemente se reutiliza en este plan de estudios en particular)… porque como he dicho, los enlaces numéricos NO se mencionan en el CCS.

Lo que no son los Estándares de Matemáticas del Common Core

1. No son «nuevas matemáticas». En comparación con muchos planes de estudio de matemáticas utilizados en la década de 2000 que hacían hincapié en los algoritmos no tradicionales, CCS es un claro movimiento hacia los algoritmos tradicionales y la memorización. Echa un vistazo a estos estándares específicos:
   

   2.OA.2
   Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del segundo grado, saber de memoria todas las sumas de dos números de un dígito.
   Nota de María: se trata de las operaciones básicas de adición, como 7 + 7 o 5 + 4.

   3.OA.7
   Multiplicar y dividir con fluidez dentro de 100, utilizando estrategias como la relación entre la multiplicación y la división (por ejemplo, sabiendo que 8 × 5 = 40, se sabe que 40 ÷ 5 = 8) o las propiedades de las operaciones. Al final del tercer grado, conocer de memoria todos los productos de dos números de una cifra.
   Nota de María: esto significa las tablas de multiplicar y las operaciones básicas de división.

   4.NBT.4
   Sumar y restar con soltura números enteros de varias cifras utilizando el algoritmo estándar.

   5.NBT.5
   Multiplicar con soltura números enteros de varias cifras utilizando el algoritmo estándar.
   Nota de María: esto no significa que los alumnos multipliquen números enteros de varias cifras sólo en 5º; eso se estudia también en 3º y 4º.

2. Los estándares no imponen estrategias extrañas ni modelos visuales a profesores y alumnos. Muchos estándares dejan en manos de los profesores y alumnos. Por ejemplo:
   

   2.NBT.5
   Suma y resta con fluidez dentro de 100 utilizando estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta.

   Nótese el «y/o» en la frase anterior. Esto significa que los profesores y los alumnos NO están limitados a utilizar ninguna estrategia específica ni se les dice que utilicen varias estrategias. El algoritmo tradicional de «préstamo» es una estrategia basada en el valor posicional por lo que se incluye aquí mismo en 2.NBT.5.

   2.NBT.9
   Explicar por qué funcionan las estrategias de adición y sustracción, utilizando el valor posicional y las propiedades de las operaciones. Las explicaciones pueden apoyarse en dibujos u objetos.

   Dice «pueden apoyarse en dibujos» pero no obliga a hacerlo, ni limita a utilizar un modelo visual o tipo de dibujo específico.

   3.OA.3
   Utilizar la multiplicación y la división dentro de 100 para resolver problemas de palabras insituaciones que implican grupos iguales, matrices y cantidades de medida, por ejemplo, utilizando dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.

   El alumno no TIENE que utilizar un dibujo. Sólo se menciona como una posibilidad.

   4.NBT.5
   Multiplicar un número entero de hasta cuatro cifras por un número entero de una cifra, y multiplicar dos números de dos cifras, utilizando estrategias basadas en el valor posicional y las propiedades de las operaciones. Ilustrar y explicar el cálculo utilizando ecuaciones, matrices rectangulares y/o modelos de áreas.

   Nota el «y/o». Ilustre el cálculo pero es suficiente con ilustrarlo utilizando ecuaciones. No TIENES que ilustrarlo usando matrices.

   Dicho esto, algunos estándares sí mencionan un modelo visual específico, como una recta numérica o un modelo de área rectangular, pero eso es menos común que dar una opción como en los estándares anteriores.

Matemáticas conceptuales

Hay algunos estándares que se adentran en el lado conceptual de las matemáticas que los profesores de primaria pueden no entender si no se les enseña lo que significan; por ejemplo:

5. NF.7b
Interpretar la división de un número entero por una fracción unitaria y calcular dichos cocientes. Por ejemplo, crear un contexto de historia para 4 ÷ (1/5), y utilizar un modelo visual de fracción para mostrar el cociente. Utilice la relación entre la multiplicación y la división para explicar que 4 ÷ (1/5) = 20 porque 20 × (1/5) = 4.

Un problema de este tipo podría ser: ¿cuántas piezas de 1/5 pies de largo se pueden cortar de una pieza de 4 pies? Un modelo visual podría mostrar 4 enteros, divididos en quintos. Entonces podemos contar que 4 enteros tienen un total de 20 quintos.

5.NF.4b
Encuentra el área de un rectángulo con longitudes laterales fraccionarias al embaldosarlo con cuadrados unitarios de las longitudes laterales fraccionarias apropiadas, y demuestra que el área es la misma que se encontraría al multiplicar las longitudes laterales. Multiplicar las longitudes laterales fraccionarias para encontrar las áreas de los rectángulos, y representar los productos de las fracciones como áreas rectangulares.

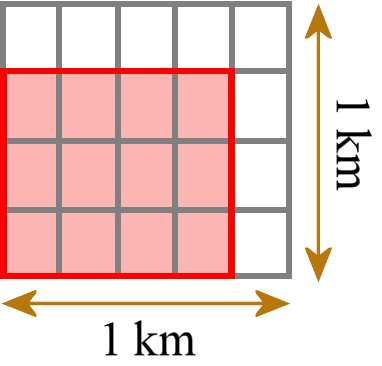Esto significa, por ejemplo, un rectángulo con longitudes laterales de 3/4 km y 4/5 km. Entonces lo embaldosamos con pequeños rectángulos unitarios (no cuadrados unitarios; aquí la propia norma tiene la terminología incorrecta) que tienen cada uno longitudes laterales de 1/4 km y 1/5 km.

Podemos contar cuántas baldosas pequeñas necesitamos. Necesitamos 12 baldosas de este tipo. Cada baldosa tiene un área de 1/20 km2, por lo que el área total es de 12/20 km2. Luego comprobamos y comparamos que obtenemos la misma respuesta que si hubiéramos multiplicado las dos longitudes de los lados utilizando la multiplicación de fracciones normal (3/4 km × 4/5 km = 12/20 km2).

Siempre he tenido este tipo de problemas en mis libros, incluso antes de que aparecieran los CCS.

Algunas personas argumentan que los niños no necesitan esa comprensión conceptual o que es demasiado difícil. Personalmente, no estoy de acuerdo. Siempre (también antes del CCS) me he esforzado por explicar los conceptos de la aritmética de fracciones para que los alumnos no acaben «siguiendo ciegamente las reglas», sólo capaces de calcular con fracciones si por casualidad recuerdan la regla correctamente. Siempre he hecho hincapié en la comprensión conceptual en matemáticas (¡como saben mis lectores!).

Pero, espero que puedas ver cómo algunas de estas cosas pueden ser desconocidas para los profesores de la escuela y los padres, y por lo tanto no es de extrañar que seguir los Estándares Básicos Comunes sea difícil para ellos.

Es mi esperanza que la serie Math Mammoth Light Blue y las unidades que vendo en mis tiendas Teachers Pay Teachers y Teachers’ Notebook puedan ayudar a esos profesores & padres que necesitan materiales alineados con los Common Core. Y como he dicho, el resto de ustedes pueden estar seguros de usarlos también. No contienen ninguna matemática «extraña» o sin sentido, sino que, como siempre, se basan simplemente en la sólida base de enseñar los conceptos de las matemáticas junto con los procedimientos.

Por María Miller