Los valores propios son un conjunto especial de escalares asociados a un sistema lineal de ecuaciones (i.e., una ecuación matricial) que a veces también se conocen como raíces características, valores característicos (Hoffman y Kunze 1971), valores propios o raíces latentes (Marcus y Minc 1988, p. 144).

La determinación de los valores propios y los vectores propios de un sistema es extremadamente importante en física e ingeniería, donde equivale a la diagonalización de matrices y surge en aplicaciones tan comunes como el análisis de estabilidad, la física de los cuerpos en rotación y las pequeñas oscilaciones de los sistemas vibratorios, por nombrar sólo algunas. Cada valor propio está emparejado con el llamado vector propio correspondiente (o, en general, un vector propio derecho y un vector propio izquierdo correspondientes; no hay una distinción análoga entre izquierda y derecha para los valores propios).

La descomposición de una matriz cuadrada en valores propios y vectores propios se conoce en este trabajo como descomposición propia, y el hecho de que esta descomposición sea siempre posible siempre que la matriz formada por los vectores propios de sea cuadrada se conoce como teorema de la descomposición propia.

El algoritmo de Lanczos es un algoritmo para calcular los valores propios y los vectores propios de grandes matrices simétricas dispersas.

Sea una transformación lineal representada por una matriz . Si hay un vector tal que

(1)

para algún escalar , entonces se llama el valor propio de con el correspondiente vector propio (derecho) .

Siendo una matriz cuadrada

(2)

con valor propio , entonces los correspondientes vectores propios satisfacen

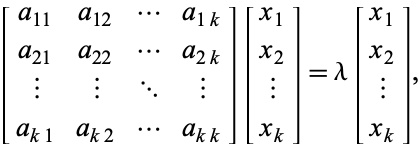(3)

que es equivalente al sistema homogéneo

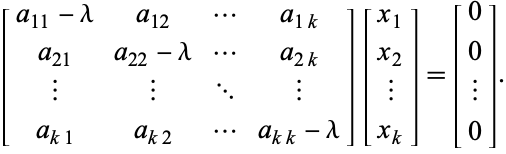(4)

La ecuación (4) puede escribirse de forma compacta como

(5)

donde es la matriz identidad. Como se muestra en la regla de Cramer, un sistema lineal de ecuaciones tiene soluciones no triviales si el determinante desaparece, por lo que las soluciones de la ecuación (5) vienen dadas por

(6)

Esta ecuación se conoce como la ecuación característica de , y el lado izquierdo se conoce como el polinomio característico.

Por ejemplo, para una matriz , los valores propios son

(7)

que surgen como las soluciones de la

(8)

Si todos los valores propios son diferentes, entonces, al introducirlos se obtienen ecuaciones independientes para las componentes de cada vector propio correspondiente, y se dice que el sistema es no degenerado. Si los valores propios son veces degenerados, entonces se dice que el sistema es degenerado y los vectores propios no son linealmente independientes. En tales casos, la restricción adicional de que los vectores propios sean ortogonales,

(9)

donde es el delta de Kronecker, puede aplicarse para obtener restricciones adicionales, permitiendo así la solución de los vectores propios.

Los valores propios pueden ser calculados en Wolfram Language utilizando Eigenvalues. Los vectores propios y los valores propios pueden devolverse juntos utilizando el comando Eigensystem.

Supongamos que conocemos el valor propio para

(10)

Añadir una constante por la matriz identidad a ,

(11)

por lo que los nuevos valores propios son iguales a los antiguos más . Multiplicando por una constante

(12)

así que los nuevos valores propios son los antiguos multiplicados por .

Consideremos ahora una transformación de similitud de . Sea el determinante de , entonces

			(13)
			(14)
			(15)

por lo que los valores propios son los mismos que para .