Obiettivi di apprendimento
- Comprendere la rappresentazione 3D degli orbitali elettronici
Un orbitale è il perfezionamento quantistico meccanico dell’orbita di Bohr. In contrasto con il suo concetto di una semplice orbita circolare con un raggio fisso, gli orbitali sono regioni di spazio derivate matematicamente con diverse probabilità di contenere un elettrone.
Un modo di rappresentare le distribuzioni di probabilità degli elettroni è stato illustrato precedentemente per l’orbitale 1s dell’idrogeno. Poiché Ψ2 dà la probabilità di trovare un elettrone in un dato volume di spazio (come un picometro cubico), un grafico di Ψ2 rispetto alla distanza dal nucleo (r) è un grafico della densità di probabilità. L’orbitale 1s è sfericamente simmetrico, quindi la probabilità di trovare un elettrone 1s in qualsiasi punto dipende solo dalla sua distanza dal nucleo. La densità di probabilità è massima a \(\(r\) = 0\) (al nucleo) e diminuisce costantemente con l’aumentare della distanza. A valori molto grandi di r, la densità di probabilità dell’elettrone è molto piccola ma non nulla.
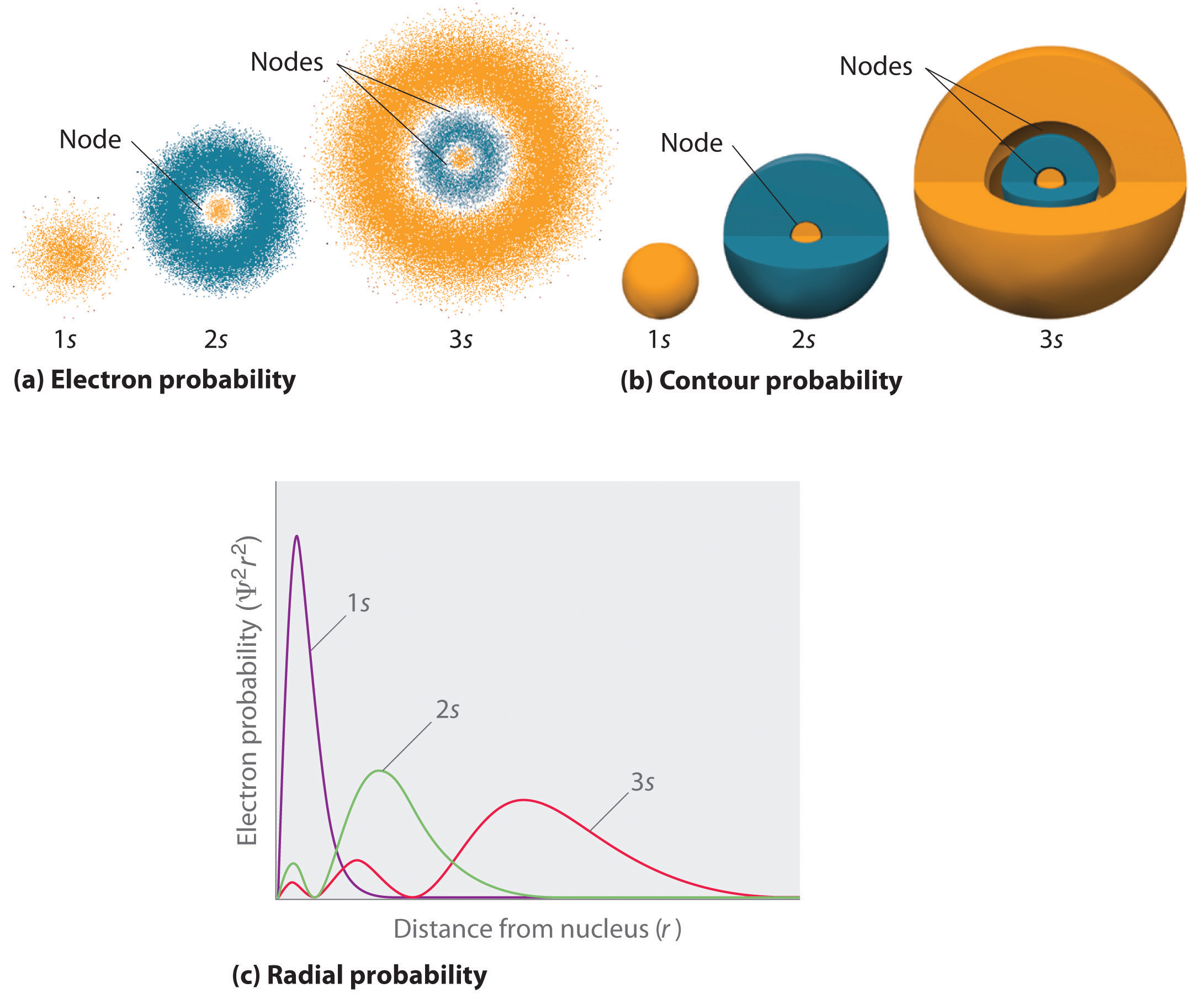
Al contrario, possiamo calcolare la probabilità radiale (la probabilità di trovare un elettrone 1s ad una distanza \(r\) dal nucleo) sommando tra loro \(r\) le probabilità che un elettrone sia in tutti i punti di una serie di x gusci sferici di raggio r1, r2, r3,…, rx – 1, rx. In effetti, stiamo dividendo l’atomo in gusci concentrici molto sottili, un po’ come gli strati di una cipolla (Figura \PageIndex{1a}\), e calcolando la probabilità di trovare un elettrone su ogni guscio sferico. Ricorda che la densità di probabilità dell’elettrone è massima a \(r\) = 0 (Figura \(\PageIndex{1b}\), quindi la densità di punti è massima per i più piccoli gusci sferici nella parte (a) della Figura \(\PageIndex{1}\. Al contrario, l’area della superficie di ogni guscio sferico è uguale a \(4πr^2\), che aumenta molto rapidamente all’aumentare di \(r\) (Figura \(\PageIndex{1c}). Poiché l’area della superficie dei gusci sferici aumenta più rapidamente con l’aumentare di \r, che la densità di probabilità degli elettroni diminuisce, il grafico della probabilità radiale ha un massimo ad una particolare distanza di \r (Figura \PageIndex{1d}). La cosa più importante è che quando \(r\) è molto piccolo, la superficie di un guscio sferico è così piccola che la probabilità totale di trovare un elettrone vicino al nucleo è molto bassa; al nucleo, la probabilità dell’elettrone svanisce (Figura \(\PageIndex{1d}}).

Fo\(r\) l’atomo di idrogeno, il picco nel grafico della probabilità radiale si verifica a \(r\) = 0,529 Å (52,9 pm), che è esattamente il raggio calcolato da Boh\(r\) per l’orbita n = 1. Così il raggio più probabile ottenuto dalla meccanica quantistica è identico al raggio calcolato dalla meccanica classica. Nel modello di Bohr, tuttavia, si supponeva che l’elettrone fosse a questa distanza il 100% del tempo, mentre nel modello di Schrödinge(r\), è a questa distanza solo per una parte del tempo. La differenza tra i due modelli è attribuibile al comportamento ondulatorio dell’elettrone e al principio di indeterminazione di Heisenberg.
La figura (\PageIndex{2}) confronta le densità di probabilità degli elettroni per gli orbitali 1s, 2s e 3s dell’idrogeno. Nota che tutti e tre sono sfericamente simmetrici. Per gli orbitali 2s e 3s, tuttavia (e per tutti gli altri orbitali s), la densità di probabilità degli elettroni non cade dolcemente all’aumentare di \(r). Invece, una serie di minimi e massimi sono osservati nei grafici di probabilità radiali (Figura 2c)). I minimi corrispondono a nodi sferici (regioni di probabilità elettronica nulla), che si alternano a regioni sferiche di probabilità elettronica non nulla. L’esistenza di questi nodi è una conseguenza dei cambiamenti di fase d’onda nella funzione d’onda Ψ.
Orbitali s (l=0)
Ci sono tre cose che accadono agli orbitali s all’aumentare di n (Figura \PageIndex{2}):
- diventano più grandi, estendendosi più lontano dal nucleo.
- Contengono più nodi. Questo è simile a un’onda stazionaria che ha regioni di ampiezza significativa separate da nodi, punti con ampiezza zero.
- Per un dato atomo, gli orbitali s diventano anche più alti in energia all’aumentare di n a causa della maggiore distanza dal nucleo.
Gli orbitali sono generalmente disegnati come superfici tridimensionali che racchiudono il 90% della densità elettronica, come è stato mostrato per gli orbitali 1s, 2s e 3s dell’idrogeno nella parte (b) della figura (\PageIndex{2}). Anche se tali disegni mostrano le dimensioni relative degli orbitali, normalmente non mostrano i nodi sferici negli orbitali 2s e 3s perché i nodi sferici si trovano all’interno della superficie del 90%. Fortunatamente, le posizioni dei nodi sferici non sono importanti per il legame chimico.
Orbitali p (l=1)
Solo gli orbitali s sono sfericamente simmetrici. All’aumentare del valore di l, il numero (r) di orbitali in un dato sottoguscio aumenta, e le forme degli orbitali diventano più complesse. Poiché il sottoguscio 2p ha l = 1, con tre valori di ml (-1, 0, e +1), ci sono tre orbitali 2p.
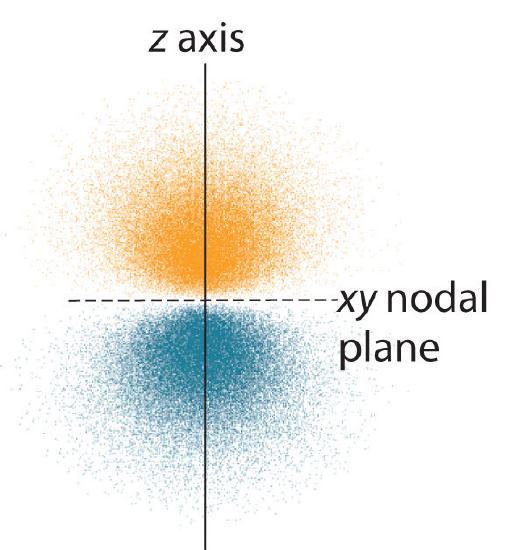
La distribuzione di probabilità degli elettroni per uno degli orbitali 2p dell’idrogeno è mostrata nella Figura \(\PageIndex{3}). Poiché questo orbitale ha due lobi di densità di elettroni disposti lungo l’asse z, con una densità di elettroni pari a zero nel piano xy (cioè, il piano xy è un piano nodale), è un orbitale \(2p_z\). Come mostrato nella figura 4, gli altri due orbitali 2p hanno forme identiche, ma giacciono rispettivamente lungo l’asse x (2p_x) e l’asse y (2p_y). Nota che ogni orbitale p ha un solo piano nodale. In ogni caso, la fase della funzione d’onda fo\(r\) ciascuno degli orbitali 2p è positiva fo\(r\) il lobo che punta lungo l’asse positivo e negativa fo\(r\) il lobo che punta lungo l’asse negativo. È importante sottolineare che questi segni corrispondono alla fase dell’onda che descrive il moto dell’elettrone, non alle cariche positive o negative.
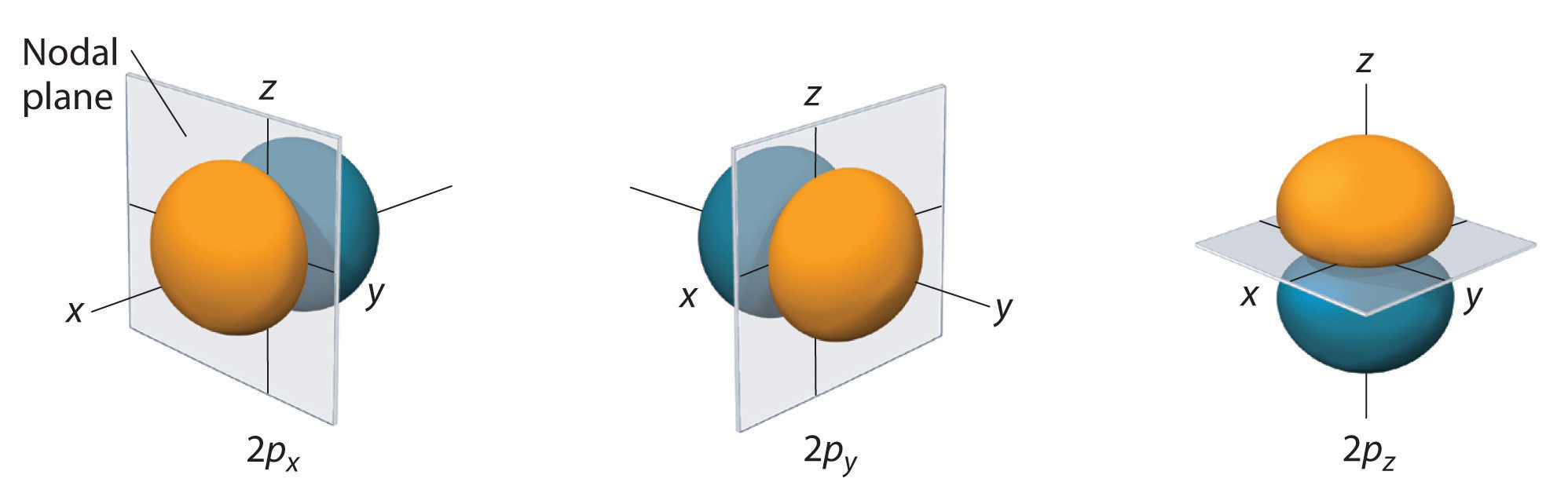
Le superfici mostrate racchiudono il 90% della probabilità totale dell’elettrone fo\(r\) gli orbitali 2px, 2py e 2pz. Ogni orbitale è orientato lungo l’asse indicato dal pedice e un piano nodale che è perpendicolare a tale asse biseca ogni orbitale 2p. La fase della funzione d’onda è positiva (arancione) nella regione dello spazio dove x, y, o\(r\) z è positiva e negativa (blu) dove x, y, o\(r\) z è negativa. Proprio come per gli orbitali s, la dimensione e la complessità degli orbitali p fo\(r\) qualsiasi atomo aumentano all’aumentare del numero quantico principale n. Le forme delle superfici di probabilità del 90% degli orbitali 3p, 4p, e degli orbitali p a più alta energia sono, comunque, essenzialmente le stesse di quelle mostrate nella Figura \(\PageIndex{4}\).
Orbitali d (l=2)
I sottogusci con l = 2 hanno cinque orbitali d; il primo guscio principale ad avere un sottoguscio d corrisponde a n = 3. I cinque orbitali d hanno valori ml di -2, -1, 0, +1, e +2.
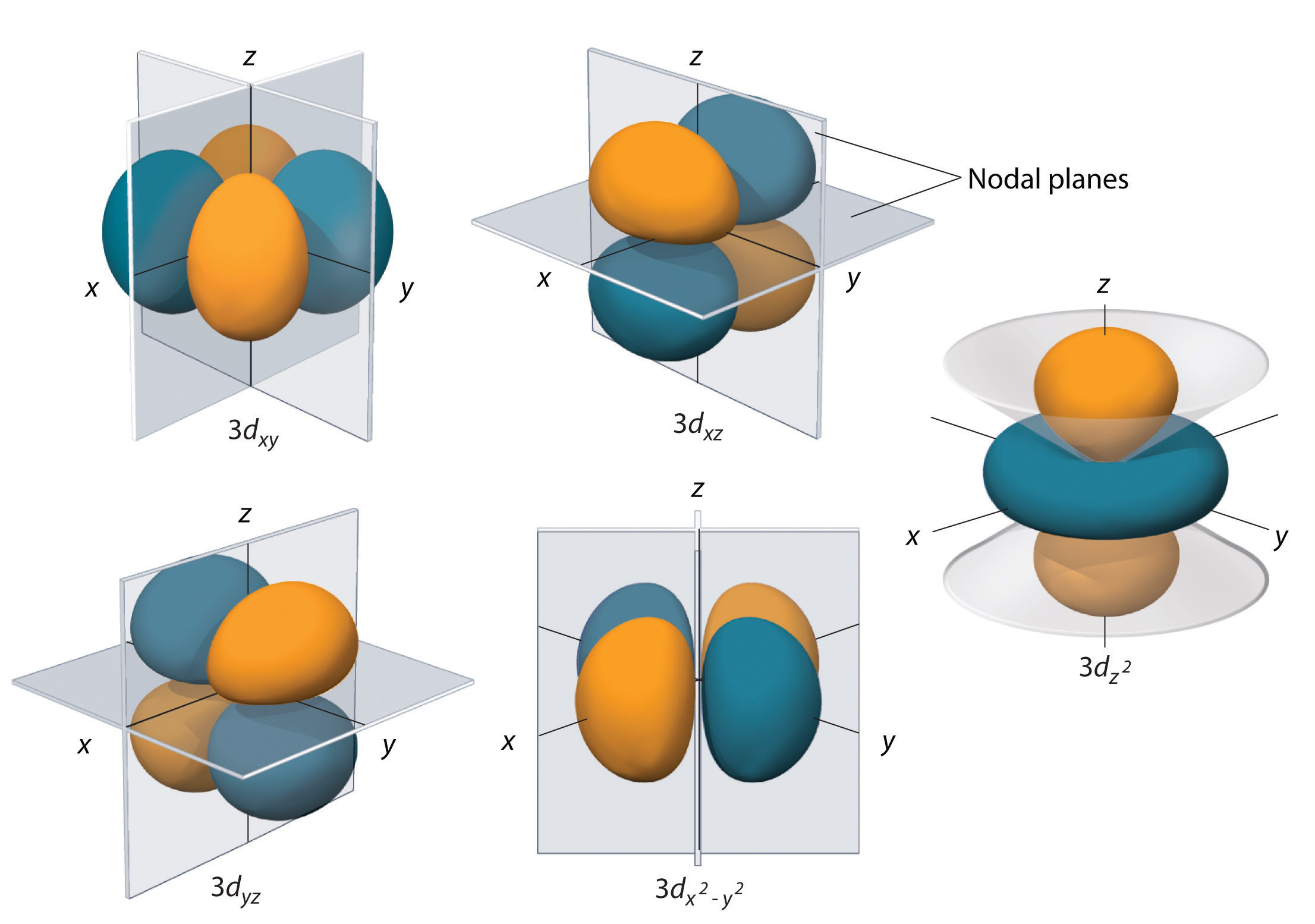
Gli orbitali 3d dell’idrogeno, mostrati nella figura \(\PageIndex{5}), hanno forme più complesse degli orbitali 2p. Tutti e cinque gli orbitali 3d contengono due superfici nodali, in confronto a un fo(r) per ogni orbitale p e zero fo(r) per ogni orbitale s. In tre degli orbitali d, i lobi della densità degli elettroni sono orientati tra i piani x e y, x e z, e y e z; questi orbitali sono indicati come gli orbitali \(3d_{xy}), \(3d_{xz}), e \(3d_{yz}), rispettivamente. Un quarto orbitale d ha lobi che giacciono lungo gli assi x e y; questo è l’orbitale \ 3d_{x^2-y^2}. Il quinto orbitale 3d, chiamato orbitale \ 3d_{z^2}, ha una forma unica: assomiglia ad un orbitale \ 2p_z\ combinato con una ciambella aggiuntiva di probabilità di elettroni che giace nel piano xy. Nonostante la sua peculiare forma, l’orbitale \ 3d_z^2} è matematicamente equivalente all’altro orbitale \ r e ha la stessa energia. A differenza degli orbitali p, la fase della funzione d’onda per gli orbitali d è la stessa per le coppie opposte di lobi. Come mostrato in figura, la fase della funzione d’onda è positiva per i due lobi dell’orbitale dz^2 che giacciono lungo l’asse z, mentre la fase della funzione d’onda è negativa per la ciambella di densità elettronica nel piano xy. Come gli orbitali s e p, all’aumentare di n, la dimensione degli orbitali d aumenta, ma le forme complessive rimangono simili a quelle rappresentate nella figura \(\PageIndex{5}).
Orbitali f (l=3)
Gusci principali con n = 4 possono avere sottogusci con l = 3 e valori ml di -3, -2, -1, 0, +1, +2, e +3. Questi sottogusci consistono di sette orbitali f. Ogni orbitale f ha tre superfici nodali, quindi le formei\(r\) sono complesse. Siccome gli orbitali f non sono particolarmente importanti per i nostri scopi, non li discutiamo ulteriormente, e gli orbitali con valori più alti di l non vengono discussi affatto.
Energie orbitali
Anche se abbiamo discusso le forme degli orbitali, abbiamo detto poco sulle energie comparative. Cominciamo la nostra discussione sulle energie orbitali considerando gli atomi o gli ioni con un solo elettrone (come l’H o l’He+).
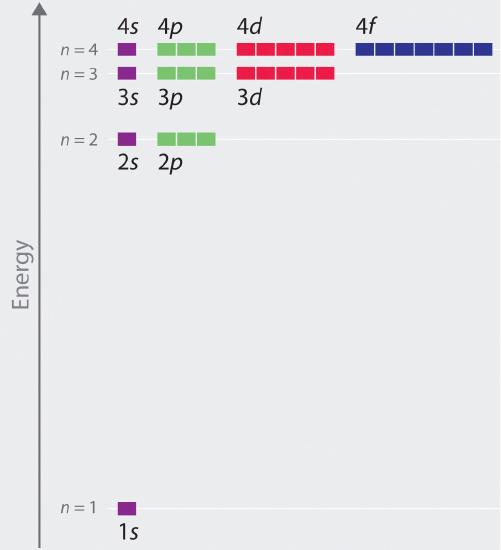
Le energie relative degli orbitali atomici con n ≤ 4 per un atomo di idrogeno sono tracciate nella figura (\PageIndex{6}); notate che le energie degli orbitali dipendono solo dal numero quantico principale n. Di conseguenza, le energie degli orbitali 2s e 2p dell’idrogeno sono le stesse; le energie degli orbitali 3s, 3p e 3d sono le stesse; e così via. La meccanica quantistica prevede che nell’atomo di idrogeno, tutti gli orbitali con lo stesso valore di n (per esempio, i tre orbitali 2p) sono degenerati, cioè hanno la stessa energia. Le energie orbitali ottenute per l’idrogeno usando la meccanica quantistica sono esattamente le stesse delle energie permesse calcolate da Boh (r). In contrasto con il modello di Bohr, tuttavia, che permetteva solo un’orbita per ogni livello energetico, la meccanica quantistica predice che ci sono 4 orbitali con diverse distribuzioni di densità di elettroni nel guscio principale n = 2 (un orbitale 2s e tre 2p), 9 nel guscio principale n = 3, e 16 nel guscio principale n = 4.I diversi valori di l e ml per i singoli orbitali all’interno di un dato guscio principale non sono importanti per capire gli spettri di emissione o di assorbimento dell’atomo di idrogeno nella maggior parte delle condizioni, ma spiegano le spaccature delle linee principali che si osservano quando gli atomi di idrogeno sono posti in un campo magnetico. La figura \PageIndex{6} mostra che i livelli di energia diventano vicini e vicini all’aumentare del valore di n, come ci si aspetta a causa della dipendenza 1/n2 delle energie orbitali.
Le energie degli orbitali in qualsiasi specie con un solo elettrone possono essere calcolate da una variazione minima dell’equazione di Bohr, che può essere estesa ad altre specie a singolo elettrone incorporando la carica del nucleo \(Z) (il numero di protoni nel nucleo):
In generale, sia l’energia che il raggio diminuiscono all’aumentare della carica del nucleo. Così gli orbitali più stabili (quelli con l’energia più bassa) sono quelli più vicini al nucleo. Ad esempio, nello stato fondamentale dell’atomo di idrogeno, il singolo elettrone è nell’orbitale 1s, mentre nel primo stato eccitato, l’atomo ha assorbito energia e l’elettrone è stato promosso a uno degli orbitali n = 2. Negli ioni con un solo elettrone, l’energia di un dato orbitale dipende solo da n, e tutti i sottogusci all’interno di un guscio principale, come gli orbitali \(p_x\), \(p_y\), e \(p_z\), sono degenerati.
Sommario
I tipi di orbitali atomici chimicamente importanti corrispondono a valori di \(ell = 0\), \(1\), \(2\) e \(3\). Gli orbitali con \(ell = 0\) sono orbitali s e sono sfericamente simmetrici, con la massima probabilità di trovare l’elettrone che si verifica al nucleo. Tutte le orbite con valori di \(n > 1\) e \(ell = 0\) contengono uno o\(r) più nodi. Gli orbitali con \(ell = 1\) sono orbitali p e contengono un piano nodale che include il nucleo, dando luogo ad una forma a manubrio. Gli orbitali con \(\ell = 2\) sono orbitali d e hanno forme più complesse con almeno due superfici nodali. Gli orbitali con \(\ell = 3\) sono orbitali f, che sono ancora più complessi.
Perché la sua distanza media dal nucleo determina l’energia di un elettrone, ogni orbitale atomico con un dato insieme di numeri quantici ha una particolare energia associata ad esso, l’energia orbitale.
Negli atomi o\(r\) ioni con un solo elettrone, tutti gli orbitali con lo stesso valore di \(n\) hanno la stessa energia (sono degenerati), e le energie dei gusci principali aumentano dolcemente all’aumentare di \(n\). Un atomo o uno ione con l’elettrone o gli elettroni nell’orbitale o negli orbitali a più bassa energia si dice che è nel suo stato di terra, mentre un atomo o uno ione in cui uno o più elettroni occupano orbitali a più alta energia si dice che è in uno stato eccitato.
Contribuenti e attribuzioni
-
Modificato da Joshua Halpern (Howard University)