Gli autovalori sono un insieme speciale di scalari associati a un sistema di equazioni lineari (es.e., un’equazione matriciale) che a volte sono anche conosciuti come radici caratteristiche, valori caratteristici (Hoffman e Kunze 1971), valori propri, o radici latenti (Marcus e Minc 1988, p. 144).

La determinazione degli autovalori e degli autovettori di un sistema è estremamente importante in fisica e in ingegneria, dove è equivalente alla diagonalizzazione della matrice e si presenta in applicazioni comuni come l’analisi della stabilità, la fisica dei corpi rotanti, e le piccole oscillazioni dei sistemi vibranti, per nominarne solo alcune. Ogni autovalore è accoppiato con un corrispondente cosiddetto autovettore (o, in generale, un corrispondente autovettore destro e un corrispondente autovettore sinistro; non esiste un’analoga distinzione tra sinistra e destra per gli autovalori).

La decomposizione di una matrice quadrata in autovalori e autovettori è nota in questo lavoro come decomposizione degli autovalori, e il fatto che questa decomposizione sia sempre possibile finché la matrice costituita dagli autovettori di è quadrata è noto come teorema della decomposizione degli autovalori.

L’algoritmo di Lanczos è un algoritmo per calcolare gli autovalori e gli autovettori per grandi matrici sparse simmetriche.

Sia una trasformazione lineare rappresentata da una matrice . Se esiste un vettore tale che

(1)

per qualche scalare , allora è detto autovalore di con corrispondente autovettore (destro) .

Posto che sia una matrice quadrata

(2)

con autovalore , allora i corrispondenti autovettori soddisfano

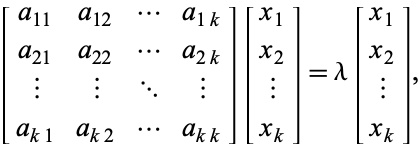(3)

che è equivalente al sistema omogeneo

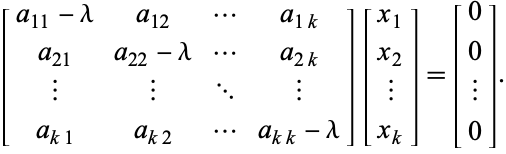(4)

L’equazione (4) può essere scritta in modo compatto come

(5)

dove è la matrice identità. Come mostrato nella regola di Cramer, un sistema lineare di equazioni ha soluzioni non banali se il determinante svanisce, quindi le soluzioni dell’equazione (5) sono date da

(6)

Questa equazione è nota come equazione caratteristica di , e il lato sinistro è noto come polinomio caratteristico.

Per esempio, per una matrice , gli autovalori sono

(7)

che nasce come soluzione della della domanda caratteristica

(8)

Se tutti gli autovalori sono diversi, allora, inserendo questi ultimi, si ottengono equazioni indipendenti per le componenti di ogni autovettore corrispondente, e il sistema è detto nondegenerato. Se gli autovalori sono degenerati, allora il sistema è detto degenerato e gli autovettori non sono linearmente indipendenti. In questi casi, il vincolo aggiuntivo che gli autovettori siano ortogonali,

(9)

dove è il delta di Kronecker, può essere applicato per ottenere vincoli aggiuntivi, permettendo così la soluzione degli autovettori.

Gli autovalori possono essere calcolati in Wolfram Language usando Eigenvalues. Gli autovettori e gli autovalori possono essere restituiti insieme usando il comando Eigensystem.

Assumiamo di conoscere l’autovalore per

(10)

Aggiungendo una costante per la matrice identità a ,

(11)

così i nuovi autovalori sono uguali ai vecchi più . Moltiplicando per una costante

(12)

così i nuovi autovalori sono i vecchi moltiplicati per . Sia il determinante di , allora

			(13)
			(14)
			(15)

per cui gli autovalori sono gli stessi di .