Come il regolatore P-Only, l’algoritmo proporzionale-integrale (PI) calcola e trasmette un segnale di uscita del regolatore (CO) ogni tempo di campionamento, T, all’elemento di controllo finale (per esempio, valvola, pompa a velocità variabile). Il CO calcolato dall’algoritmo PI è influenzato dai parametri di regolazione del regolatore e dall’errore del regolatore, e(t).
I regolatori PI hanno due parametri di regolazione da regolare. Anche se questo li rende più impegnativi da sintonizzare rispetto a un regolatore P-only, non sono così complessi come il regolatore PID a tre parametri.
L’azione integrale permette ai regolatori PI di eliminare l’offset, una grande debolezza di un regolatore P-only. Così, i controllori PI forniscono un equilibrio di complessità e capacità che li rende di gran lunga l’algoritmo più usato nelle applicazioni di controllo del processo.
L’algoritmo PI
Mentre diversi fornitori presentano lo stesso algoritmo in forme diverse, qui esploriamo quello che è variamente descritto come la forma dipendente, ideale, continua, di posizione:
![]()
dove:
CO = segnale di uscita del regolatore (il filo in uscita)
CObias = bias del regolatore o valore nullo; impostato dal trasferimento senza urti come spiegato di seguito
e(t) = errore corrente del regolatore, definito come SP – PV
SP = set point
PV = variabile di processo misurata (il filo in)
Kc = guadagno del regolatore, un parametro di regolazione
Ti = tempo di reset, un parametro di regolazione
I primi due termini a destra del segno uguale sono identici al regolatore P-Only menzionato all’inizio di questo articolo.
Il modo integrale del regolatore è l’ultimo termine dell’equazione. La sua funzione è quella di integrare o sommare continuamente l’errore del controllore, e(t), nel tempo.
Alcune cose che dovremmo sapere sul parametro di regolazione del tempo di reset, Ti:
| ▪ | Fornisce un peso separato al termine integrale così l’influenza dell’azione integrale può essere regolata indipendentemente. |
| ▪ | Si trova nel denominatore quindi i valori più piccoli forniscono un peso maggiore al (cioè aumentare l’influenza del) termine integrale. |
| ▪ | Ha unità di tempo quindi è sempre positivo. |
Funzione del termine proporzionale
Come per il regolatore P-Only, il termine proporzionale del regolatore PI, Kc-e(t), aggiunge o sottrae da CObias in base alla dimensione dell’errore del regolatore e(t) ad ogni tempo t.
Quando e(t) cresce o si riduce, la quantità aggiunta a CObias cresce o si riduce immediatamente e proporzionalmente. La storia passata e la traiettoria attuale dell’errore del controllore non hanno alcuna influenza sul calcolo del termine proporzionale.
Il grafico qui sotto (cliccare per una vista più grande) illustra questa idea per una risposta di set point. L’errore usato nel calcolo proporzionale è mostrato sul grafico:
▪ Al tempo t = 25 min, e(25) = 60-56 = 4
▪ Al tempo t = 40 min, e(40) = 60-62 = -2
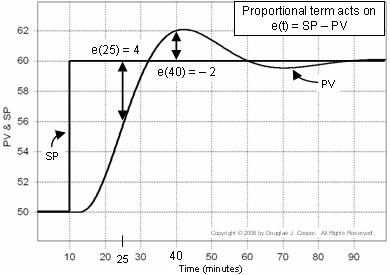
Ricordando che l’errore del regolatore e(t) = SP – PV, piuttosto che vedere PV e SP come tracce separate come facciamo sopra, possiamo calcolare e tracciare e(t) in ogni punto del tempo t.
Di seguito (fare clic per una visualizzazione più grande) sono i dati identici a quelli sopra, solo che sono rifatti come un grafico di e(t) stesso. Notate che nel grafico sopra, PV = SP = 50 per i primi 10 minuti, mentre nel grafico dell’errore sotto, e(t) = 0 per lo stesso periodo di tempo.
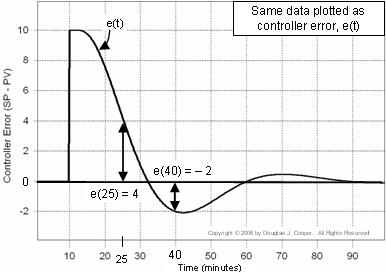
Questo grafico è utile perché ci aiuta a visualizzare come l’errore del controllore cambia continuamente dimensione e segno con il passare del tempo.
Funzione del termine integrale
Mentre il termine proporzionale considera la dimensione attuale di e(t) solo al momento del calcolo del controllore, il termine integrale considera la storia dell’errore, o quanto a lungo e quanto lontano la variabile di processo misurata è stata dal set point nel tempo.
L’integrazione è una somma continua. L’integrazione dell’errore nel tempo significa che sommiamo l’intera storia dell’errore del regolatore fino al momento attuale, partendo da quando il regolatore è stato commutato per la prima volta in automatico.
L’errore del regolatore è e(t) = SP – PV. Nel grafico qui sotto (clicca per una visualizzazione più grande), la somma integrale dell’errore è calcolata come le aree ombreggiate tra le tracce SP e PV.
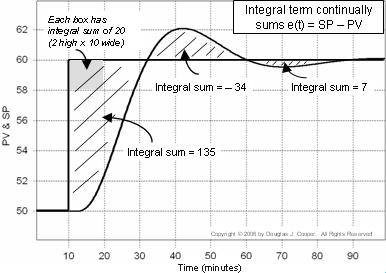
Ogni casella nel grafico ha una somma integrale di 20 (2 alte per 10 larghe). Se contiamo il numero di caselle (comprese le frazioni di caselle) contenute nelle aree ombreggiate, possiamo calcolare la somma integrale dell’errore.
Quindi quando il PV attraversa per la prima volta il set point intorno a t = 32, la somma integrale è cresciuta a circa 135. Scriviamo il termine integrale del regolatore PI come:
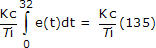
Siccome è l’errore del regolatore che guida il calcolo, otteniamo una visione diretta della situazione da un grafico dell’errore del regolatore come mostrato qui sotto (cliccare per una vista grande):

Nota che l’integrale di ogni parte ombreggiata ha lo stesso segno dell’errore. Poiché la somma integrale inizia ad accumularsi quando il regolatore viene messo in automatico per la prima volta, la somma integrale totale cresce finché e(t) è positivo e si riduce quando è negativo.
Al tempo t = 60 min sui grafici, la somma integrale è 135 – 34 = 101. La risposta è in gran parte risolta a t = 90 min, e la somma integrale è allora 135 – 34 + 7 = 108.
L’azione integrale elimina l’offset
La frase precedente fa un’osservazione sottile ma molto importante. La risposta è in gran parte completa al tempo t = 90 min, eppure la somma integrale di tutti gli errori non è zero.
In questo esempio, la somma integrale ha un valore finale o residuo di 108. È questo valore residuo che permette all’azione integrale del regolatore PI di eliminare l’offset.
Come discusso in un articolo precedente, la maggior parte dei processi sotto controllo solo P sperimenta l’offset durante il funzionamento normale. L’offset è un valore sostenuto per l’errore del controllore (cioè, PV non è uguale a SP allo stato stazionario).
Riconosciamo dal controllore P-Only:
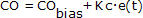
che CO sarà sempre uguale a CObias a meno che non aggiungiamo o sottraiamo qualcosa da esso.
L’unico modo per avere qualcosa da aggiungere o sottrarre da CObias nell’equazione P-Only sopra è se e(t) non è zero. Se e(t) non è costante a zero, allora PV non è uguale a SP e abbiamo un offset.
Tuttavia, con il controllore PI:
![]()
ora sappiamo che la somma integrale dell’errore può avere un valore finale o residuo dopo che una risposta è completa. Questo è importante perché significa che e(t) può essere zero, eppure possiamo ancora avere qualcosa da aggiungere o sottrarre da CObias per formare l’uscita finale del controllore, CO.
Quindi, finché c’è qualche errore (finché e(t) non è zero), il termine integrale crescerà o si ridurrà di dimensione per avere un impatto su CO. I cambiamenti in CO cesseranno solo quando PV sarà uguale a SP (quando e(t) = 0) per un periodo di tempo sostenuto.
A quel punto, il termine integrale può avere un valore residuo come appena discusso. Questo valore residuo dall’integrazione, quando aggiunto a CObias, crea essenzialmente un nuovo valore di bias complessivo che corrisponde al nuovo livello di funzionamento.
In effetti, l’azione integrale resetta continuamente il valore di bias per eliminare l’offset al variare del livello operativo.
Sfide del controllo PI
Ci sono delle sfide nell’impiego dell’algoritmo PI:
| ▪ | I due parametri di regolazione interagiscono tra loro e la loro influenza deve essere equilibrata dal progettista. |
| ▪ | Il termine integrale tende ad aumentare il comportamento oscillatorio o di rotolamento della risposta del processo. |
Perché i due parametri di regolazione interagiscono tra loro, può essere difficile arrivare ai “migliori” valori di regolazione. Il valore e l’importanza del nostro progetto e della nostra ricetta di regolazione aumentano man mano che il controllore diventa più complesso.
Inizializzando il controllore per il trasferimento senza protuberanze
Quando passiamo qualsiasi controllore dalla modalità manuale a quella automatica (da anello aperto ad anello chiuso), vogliamo che il risultato sia senza problemi. Cioè, non vogliamo che la commutazione causi azioni di controllo improvvise che impattino o interrompano il nostro processo
Abbiamo ottenuto questo risultato desiderato alla commutazione inizializzando la somma integrale dell’errore del controllore a zero. Inoltre, il set point e il valore di bias del regolatore sono inizializzati impostando:
▪ SP uguale all’attuale PV
▪ CObias uguale all’attuale CO
Con la somma integrale dell’errore impostata a zero, non c’è nulla da aggiungere o sottrarre da CObias che causerebbe un cambiamento improvviso nell’uscita corrente del regolatore. Con il set point uguale alla variabile di processo misurata, non c’è nessun errore a guidare un cambiamento nel nostro CO. E con il bias del regolatore impostato sul nostro valore corrente di CO, siamo preparati per default a mantenere il funzionamento corrente.
Quindi, quando passiamo dalla modalità manuale a quella automatica, abbiamo un “trasferimento senza urti” senza sorprese. Questo è un risultato che tutti apprezzano.
Tempo di reset rispetto al tasso di reset
Diversi fornitori presentano i loro algoritmi di controllo in forme leggermente diverse. Alcuni usano la banda proporzionale piuttosto che il guadagno del controllore. Inoltre, alcuni usano la velocità di reset, Tr, invece del tempo di reset. Questi sono semplicemente l’inverso l’uno dell’altro:
Tr = 1/Ti
Non importa come sono espressi i parametri di regolazione, gli algoritmi PI sono tutti ugualmente capaci.
Ma è fondamentale conoscere il vostro produttore prima di iniziare a regolare il vostro regolatore perché i valori dei parametri devono essere abbinati alla vostra particolare forma di algoritmo.I software commerciali per la progettazione e la messa a punto del controllore affronteranno automaticamente questo problema per voi.
Implementazione di un controllore PI
Esaminiamo la progettazione, la messa a punto e l’implementazione del controllore PI sullo scambiatore di calore in questo articolo e sui serbatoi drenati per gravità in questo articolo.