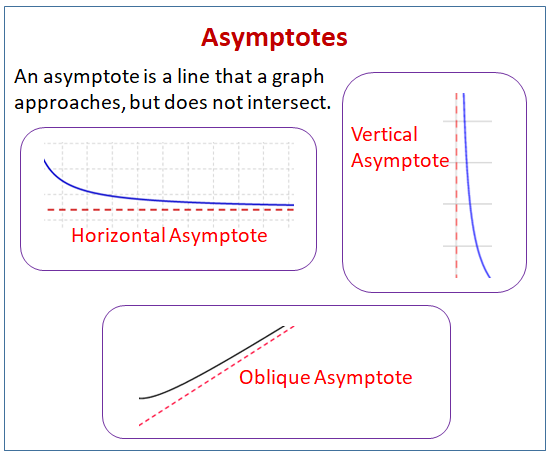
Un asintoto è una linea a cui un grafico si avvicina, ma non si interseca.
In questa lezione, impareremo come trovare gli asintoti verticali, gli asintoti orizzontali e gli asintoti obliqui di funzioni razionali.
Temi correlati:
Altre lezioni di Calcolo

Il seguente diagramma mostra i diversi tipi di asintoti: asintoti orizzontali, asintoti verticali e asintoti obliqui. Scorri la pagina per altri esempi e soluzioni su come trovare gli asintoti.

Come determinare l’asintoto verticale?

Metodo 1: Usa la definizione di asintoto verticale

La retta x = a è chiamata asintoto verticale della curva y = f(x) se almeno una delle seguenti affermazioni è vera.

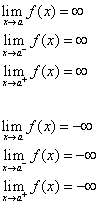
Metodo 2:

Per le funzioni razionali, gli asintoti verticali sono linee verticali che corrispondono agli zeri del denominatore.
Data la funzione razionale, f(x)

Passo 1: scrivere f(x) in forma ridotta

Passo 2: se x – c è un fattore nel denominatore allora x = c è l’asintoto verticale.

Esempio:

Trova gli asintoti verticali di

Soluzione:

Metodo 1: Usa la definizione di asintoto verticale.

Se x è vicino a 3 ma più grande di 3, allora il denominatore x – 3 è un piccolo numero positivo e 2x è vicino a 8. Quindi, è un grande numero positivo.

Intuitivamente, vediamo che

Similmente, se x è vicino a 3 ma più piccolo di 3, allora x – 3 è un piccolo numero negativo e 2x è vicino a 8. Quindi, è un grande numero negativo.

La linea x = 3 è l’asintoto verticale.

Metodo 2:

Passo 1: f(x) è già in forma ridotta.

Passo 2: Il denominatore è x – 3, e quindi l’asintoto verticale è a x = 3.

Trovare gli asintoti verticali delle funzioni razionali

Cosa cercare per trovare gli asintoti verticali delle funzioni razionali.

• Mostra le soluzioni passo dopo passo

Asintoti verticali delle funzioni razionali: Modo rapido per trovarli

Esempio di come trovare gli asintoti verticali delle funzioni razionali.

• Mostra soluzioni passo a passo

Come trovare gli asintoti verticali delle funzioni razionali

• Mostra soluzioni passo a passo

Come determinare l’asintoto orizzontale?

Metodo 1: Usare la definizione di Asintoto orizzontale

La retta y = L è detta asintoto orizzontale della curva y = f(x) se o

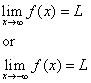
Metodo 2:

Per la funzione razionale, f(x)

Se il grado di x nel numeratore è minore del grado di x nel denominatore allora y = 0 è l’asintoto orizzontale.

Se il grado di x nel numeratore è uguale al grado di x nel denominatore allora y = c dove c si ottiene dividendo i coefficienti principali.

Esempio:

Trovare gli asintoti orizzontali e verticali della funzione.

Soluzione:

Metodo 1:

Dividere sia il numeratore che il denominatore per x.

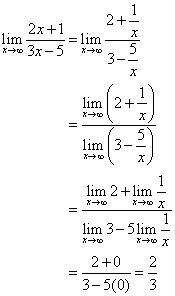
La linea è l’asintoto orizzontale.

Metodo 2:

Il grado di x nel numeratore è uguale al grado di x nel denominatore.

Dividendo i coefficienti principali si ottiene

La linea è l’asintoto orizzontale.

Scarto per trovare gli asintoti orizzontali delle funzioni razionali

Un paio di trucchi che rendono molto facile trovare gli asintoti orizzontali delle funzioni razionali

• Mostra le soluzioni passo dopo passo

Questo video darà una panoramica di base degli asintoti orizzontali. Determineremo se le funzioni razionali date hanno asintoti orizzontali e quali sono.

• Show Step-by-step Solutions

Questo video entrerà in ulteriori dettagli sulle regole degli asintoti orizzontali.

• Show Step-by-step Solutions

Asintototo obliquo o asintoto inclinato

Alcune curve hanno asintoti che sono obliqui, cioè né orizzontali né verticali.

Se allora la retta y = mx + b si chiama asintoto obliquo o inclinato perché le distanze verticali tra la curva y = f(x) e la retta y = mx + b si avvicinano a 0.

Per le funzioni razionali, gli asintoti obliqui si hanno quando il grado del numeratore è uno in più del grado del denominatore. In tal caso l’equazione dell’asintoto obliquo può essere trovata con la divisione lunga.

Esempio:

Trovare gli asintoti della funzione

Soluzione:

Siccome il denominatore x2 + 1 non è mai 0, non c’è un asintoto verticale.

Siccome il grado di x nel numeratore è maggiore del grado di x nel denominatore non c’è un asintoto orizzontale.

Siccome il grado di x nel numeratore è uno maggiore del grado di x nel denominatore possiamo usare la divisione lunga per ottenere l’asintoto obliquo.

Quindi, la retta y = x è l’asintoto obliquo.

Trovare gli asintoti obliqui delle funzioni razionali

Questo video descrive quando una funzione razionale ha un asintoto obliquo, descrive brevemente cos’è un asintoto obliquo e poi fa due esempi.

• Mostra le soluzioni passo dopo passo

Trovare gli asintoti di una funzione razionale (verticale, orizzontale e obliqua)

Questo video mostra come trovare gli asintoti verticali e gli asintoti obliqui di una funzione razionale.

• Mostra le soluzioni passo dopo passo

Trovare tutti gli asintoti di una funzione razionale (verticale, orizzontale, obliqua/inclinata)

Qui guardiamo una funzione e troviamo l’asintoto verticale e concludiamo anche che non ci sono asintoti orizzontali, ma che un asintoto obliquo esiste. Usiamo quindi la divisione lunga per trovare l’asintoto obliquo.

• Mostra le soluzioni passo dopo passo

Prova la calcolatrice gratuita Mathway e il risolutore di problemi qui sotto per praticare vari argomenti di matematica. Prova gli esempi dati, o scrivi il tuo problema e controlla la tua risposta con le spiegazioni passo dopo passo.