
Galileo è spesso considerato il padre della scienza moderna. Fu colui che mise insieme i principi di esperimento, teoria e matematica in una struttura standard. Probabilmente più di chiunque altro Galileo è stato il responsabile dello sviluppo della scienza moderna.
Si dice che Galileo lasciò cadere due palle d’acciaio di massa diversa, ma dello stesso materiale dalla torre pendente di Pisa e atterrarono nello stesso momento. Ciò che è notevole di questo esperimento è che ha inaugurato un nuovo metodo di fare scienza in cui si conduce un esperimento per testare un’ipotesi. Ha dimostrato che dobbiamo fare di più che pensare che qualcosa sia vero, ma dobbiamo anche provarlo.

Galileo trovò un interessante paradosso mentre era a capo del Dipartimento di Matematica dell’Università di Pisa.
Definizione: Un paradosso, noto anche come antinomia, è un’affermazione logicamente autocontraddittoria o un’affermazione che va contro le proprie aspettative. (Wikipedia). (Greco: “para” = oltre, “doxa” = credenza)
Il paradosso di Galileo consisteva nel determinare se due insiemi contenenti infiniti oggetti sono equivalenti tra loro. Per esempio, sia P l’insieme dei numeri interi positivi dove P= {0,1,2,3,…} ed E l’insieme dei numeri pari dove E = {0,2,4,6,…}. Galileo sosteneva che le dimensioni di questi due insiemi saranno uguali perché possiamo accoppiare ogni numero intero positivo dell’insieme P con i numeri pari dell’insieme E.

Come fa la dimensione dei due insiemi ad essere la stessa quando un numero “minore” appare in E? Questo fu chiamato il paradosso di Galileo e iniziò un nuovo dibattito sul concetto di infinito.
Dopo Galileo, il suo studente Evangelista Torricelli divenne il capo del Dipartimento di Matematica dell’Università di Pisa. Potreste averlo sentito per i suoi lavori sulla pressione atmosferica e l’invenzione del barometro. Poiché Toricelli si interessa anche di matematica, si chiede:
È possibile avere un oggetto con un volume finito e una superficie infinita? In primo luogo, una cosa del genere sembra improbabile per la maggior parte di noi. Tuttavia, la matematica ci dice che una cosa del genere potrebbe accadere. Torricelli stesso ha risposto alla sua domanda e ha scoperto la Tromba di Toricelli la cui superficie è infinita, ma il cui volume è finito. La sua scoperta vista come un paradosso “incredibile”.
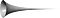
A proposito, c’è una regola essenziale nella filosofia della matematica: qualsiasi epoca di filosofia o matematica si tratti, è legata alla storia, cultura e religione di quella regione. Ecco perché chiamano la tromba di Toricelli anche il Corno di Gabriele. Si fa qui un riferimento alla Bibbia perché i cristiani credono che l’angelo, Gabriele, soffierà il corno nel giorno del giudizio.
Come si forma dunque la tromba di Toricelli? Tutti sappiamo come fare il grafico di y=x. Se si traccia il grafico dell’equazione y=1/x dove x è maggiore o uguale a 1 invece, il grafico sarà come questo:
Quando prendiamo il grafico di y=1/x e lo ruotiamo intorno all’asse x, vediamo la tromba di Toricelli.

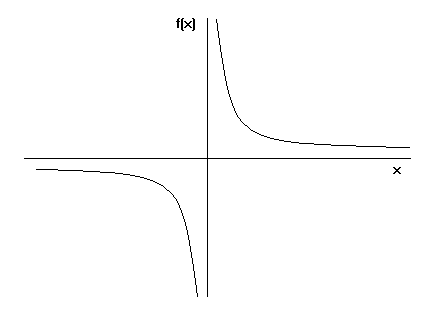
Fortunatamente, abbiamo in mano formule matematiche per calcolare l’area e il volume della tromba di Toricelli. Quando usiamo la formula di integrazione qui sotto per il volume della tromba, otteniamo una quantità finita.
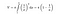
Tuttavia, quando applichiamo la formula di integrazione per la superficie della tromba, questa volta, la superficie di essa diventa infinita. Non è interessante questo risultato?
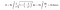
Siccome il volume della tromba di Toricelli è finito, possiamo riempirla con una quantità finita di vernice. Per esempio, supponiamo che il suo volume sia di 100 litri. Vado da Home Depot, compro 100 litri di vernice e la riempio. Tuttavia, ciò che rende questo interessante è che avrò dipinto la superficie infinita con quei 100 litri di vernice. Oggi la maggior parte delle persone chiama questo paradosso “il paradosso del pittore”.
Houston, abbiamo un problema qui! La situazione che è impossibile in pratica diventa possibile in matematica. Allora, come può essere reale la tromba di Torricelli? Oppure, come possiamo far coincidere precisamente tutti gli elementi degli insiemi mentre uno degli insiemi è un sottoinsieme di un altro nell’esempio di Galileo?
La ragione di tutti questi conflitti è che il concetto di infinito non è simile ad altri concetti che conosciamo, e questo confonde molte persone. Galileo dice per il suo paradosso,
“Sì, amico mio, esiste l’infinito. È inutile obiettare. Gli insiemi su cui sto lavorando sono esempi di insiemi chiusi che implicano l’infinito. Partono da un punto e vanno all’infinito, eppure sono ancora insiemi. Tuttavia, i miei commenti e concetti sull’infinito devono essere diversi da quelli che userei per le grandezze finite. Se si tratta di grandezze finite, si può dire che 3 chili sono meno di 5 chili, o che 32 metri sono più lunghi di 7 metri. Ma quando si tratta di infinito, non si può dire che questo infinito è più grande, più piccolo o uguale a quello.”
Questa era la soluzione di Galileo nel 1600.
Purtroppo, la soluzione di Galileo aveva iniziato un nuovo dibattito sull’infinito. Matematici e filosofi non riuscirono a trovare un accordo su una risposta specifica fino a quando Cantor condivise la sua “teoria degli insiemi”, che gli studenti imparano oggi nella scuola elementare.
Possiamo storicizzare periodicamente lo sviluppo dell’idea di infinito. È emersa per la prima volta dagli Eleatici, che era una scuola di filosofia presocratica fondata da Parmenide all’inizio del V secolo a.C. nell’antica città di Elea. C’erano tre grandi filosofi in questa scuola, come Zenone, Senofane e Parmenide. In questa scuola, la filosofia accettata era che l’esistenza era singolare e non c’era pluralità. Zenone era famoso per i suoi paradossi sull’infinito agli Eleatici. Più tardi, nel 300 a.C., Aristoteles sorse e propose una coppia di concetti per spiegare i paradossi di Zenone, che erano l’infinito potenziale e l’infinito effettivo.
L’infinito potenziale è un gruppo di numeri o un gruppo di “cose” che continua senza terminare, andando avanti o ripetendosi più e più volte senza un punto finale riconoscibile.
L’infinito reale coinvolge insiemi o “cose” senza fine all’interno di uno spazio che ha un inizio e una fine; è una serie che è tecnicamente “completata” ma consiste di un numero infinito di membri.
Aristotele credeva che non ci fosse un infinito reale. Questa idea di Aristotele ha dominato il mondo della filosofia fino al 1600. Poi filosofi come Cusa e Bruno sostennero che esiste l’infinito reale, ma non possiamo dargli un senso. Dopo Cusa e Bruno, il grande pensatore Spinoza si unì all’argomento.
Spinoza disse che potevamo capire il concetto di infinito e classificarli in grandezza. Tuttavia, ha anche affermato che non poteva fare i conti su di essi. Per esempio, poteva aggiungere 3 a 5, ma non poteva aggiungere un infinito ad un altro.
Finalmente, per finire quei dibattiti, si presentò un bell’uomo, Georg Cantor e fondò la teoria degli insiemi, che è ancora la base della matematica. Con la sua teoria degli insiemi ha posto il punto finale nelle discussioni sull’infinito.
Ha dimostrato che un insieme infinito sarebbe più grande o più piccolo di un altro insieme infinito. Inoltre, Cantor sostenne che potevamo sommare e moltiplicare gli insiemi infiniti. Fino a quel momento, gli uomini avevano seguito le idee di Aristotele sull’infinito. Secondo Aristotele, se moltiplicassimo il numero 3 per l’infinito, sarebbe di nuovo infinito. L’infinito inghiottirebbe tutto. Basandosi su questo, sosteneva che ci sarebbe stato solo un infinito potenziale, non un infinito reale.
Tuttavia, Cantor ci ha dimostrato il contrario dell’idea di Aristotele con la teoria degli insiemi. Se aggiungiamo uno a un insieme infinito, non sarà più lo stesso insieme. Ha cercato di confrontare gli infiniti. Per esempio, Cantor dimostrò che l’insieme di tutte le funzioni da (0,1)→ℕ è numerabile. Così definì una funzione uno-a-uno e onto dall’intervallo (0,1) ai numeri naturali.
In altre parole, dimostrò che tutti i numeri naturali possono stare tra 0 e 1 perché c’erano infiniti numeri razionali tra 0-1, e questi infiniti possono essere accoppiati. Poi fece qualcosa di ancora più pericoloso che trovare due infiniti uguali. Ha confrontato l’infinito dei numeri reali con l’infinito dei numeri naturali e ha trovato che l’infinito dei numeri reali è maggiore dell’altro. Guardò persino la sua prova e disse al suo amico Dedekind: “Lo vedo, ma nemmeno io ci credo…”.
Cantor era anche un matematico con preoccupazioni filosofiche e religiose molto serie. Mentre sviluppava la teoria degli insiemi, disse: “Dio mi ha dettato la teoria degli insiemi”.
La teoria degli insiemi non era ampiamente accettata quando fu sviluppata. Le aziende non assumevano nemmeno Cantor per nessun lavoro. Un matematico, Henri Poincaré, una volta disse: “Le idee di questo Cantor sono una brutta malattia che si attacca al colletto della matematica. E la matematica lo curerà un giorno”. Cantor dovette andare in un ospedale psichiatrico per un po’ e lì morì. Ma oggi lo consideriamo un genio.
Cantor era un uomo solo ai confini dell’infinito. Ha citato la Bibbia all’inizio del suo articolo sui numeri transfiniti: “Tutto ciò che è nascosto sarà portato alla luce”
.