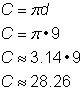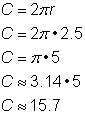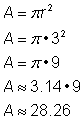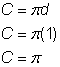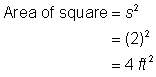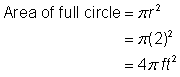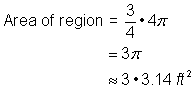Circoli
Obiettivo(i) di apprendimento
– Identificare le proprietà dei cerchi.
– Trovare la circonferenza di un cerchio.
– Trovare l’area di un cerchio.
– Trovare l’area e il perimetro di figure geometriche composte.
Introduzione
I cerchi sono una forma comune. Li vedi dappertutto: le ruote di un’automobile, i frisbee che passano nell’aria, i compact disc che trasmettono dati. Questi sono tutti cerchi.
Un cerchio è una figura bidimensionale proprio come i poligoni e i quadrilateri. Tuttavia, i cerchi sono misurati in modo diverso rispetto a queste altre forme – devi persino usare alcuni termini diversi per descriverli. Diamo un’occhiata a questa forma interessante.
Proprietà dei cerchi
Un cerchio rappresenta un insieme di punti, tutti alla stessa distanza da un punto fisso centrale. Questo punto fisso è chiamato centro. La distanza dal centro del cerchio a qualsiasi punto del cerchio è chiamata raggio.
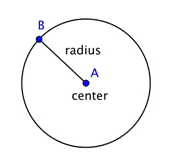
Quando due raggi (il plurale di raggio) sono messi insieme per formare un segmento di linea attraverso il cerchio, si ha un diametro. Il diametro di un cerchio passa per il centro del cerchio e ha i suoi punti finali sul cerchio stesso.
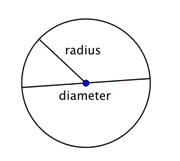
Il diametro di qualsiasi cerchio è due volte la lunghezza del raggio di quel cerchio. Può essere rappresentato dall’espressione 2r, o “due volte il raggio”. Quindi se conosci il raggio di un cerchio, puoi moltiplicarlo per 2 per trovare il diametro; questo significa anche che se conosci il diametro di un cerchio, puoi dividere per 2 per trovare il raggio.
|
Esempio |
||
|
Problema |
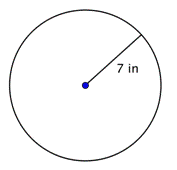
Trova il diametro del cerchio.
|
|
|
d = 2r d = 2(7) d = 14 |
Il diametro è due volte il raggio, o 2r. Il raggio di questo cerchio è 7 pollici, quindi il diametro è 2(7) = 14 pollici. |
|
|
Risposta |
Il diametro è 14 pollici. |
|
|
Esempio |
||
|
Problema |
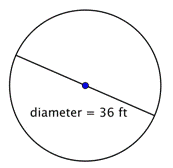
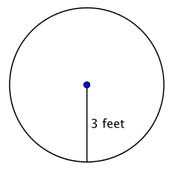
Trova il raggio del cerchio.
|
|
|
|
Il raggio è metà del diametro, ovvero |
|
|
Risposta |
Il raggio è 18 piedi. |
|
Circonferenza
La distanza intorno a un cerchio è chiamata circonferenza. (Ricordiamo che la distanza intorno a un poligono è il perimetro.)
Una proprietà interessante dei cerchi è che il rapporto tra la circonferenza di un cerchio e il suo diametro è lo stesso per tutti i cerchi. Non importa la dimensione del cerchio, il rapporto tra la circonferenza e il diametro sarà lo stesso.
Di seguito sono fornite alcune misure reali di diversi oggetti. Le misure sono accurate al millimetro o al quarto di pollice più vicino (a seconda dell’unità di misura utilizzata). Guarda il rapporto tra la circonferenza e il diametro per ognuno di essi – anche se gli oggetti sono diversi, il rapporto per ognuno è approssimativamente lo stesso.
|
Item |
Circonferenza (C) (arrotondata al centesimo più vicino) |
Diametro (d) |
Ratio |
|
Cup |
253 mm |
79 mm |
|
|
Quarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
La circonferenza e il diametro sono misure approssimative, poiché non esiste un modo preciso per misurare esattamente queste dimensioni. Se foste in grado di misurarle più precisamente, tuttavia, trovereste che il rapporto ![]() si sposterebbe verso 3,14 per ciascuno degli elementi dati. Il nome matematico del rapporto
si sposterebbe verso 3,14 per ciascuno degli elementi dati. Il nome matematico del rapporto ![]() è pi greco, ed è rappresentato dalla lettera greca
è pi greco, ed è rappresentato dalla lettera greca ![]() .
.
![]() è un decimale non terminante e non ripetitivo, quindi è impossibile scriverlo completamente. Le prime 10 cifre di
è un decimale non terminante e non ripetitivo, quindi è impossibile scriverlo completamente. Le prime 10 cifre di ![]() sono 3,141592653; è spesso arrotondato a 3,14 o stimato come la frazione
sono 3,141592653; è spesso arrotondato a 3,14 o stimato come la frazione ![]() . Si noti che sia 3,14 che
. Si noti che sia 3,14 che ![]() sono approssimazioni di
sono approssimazioni di![]() , e sono usati nei calcoli in cui non è importante essere precisi.
, e sono usati nei calcoli in cui non è importante essere precisi.
Siccome si sa che il rapporto tra circonferenza e diametro (o ![]() ) è coerente per tutti i cerchi, si può usare questo numero per trovare la circonferenza di un cerchio se si conosce il suo diametro.
) è coerente per tutti i cerchi, si può usare questo numero per trovare la circonferenza di un cerchio se si conosce il suo diametro.
![]() =
= ![]() , quindi C =
, quindi C = ![]() d
d
Inoltre, poiché d = 2r, allora C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Circonferenza di un cerchio
Per trovare la circonferenza (C) di un cerchio, usa una delle seguenti formule:
Se conosci il diametro (d) di un cerchio: ![]()
Se si conosce il raggio (r) di un cerchio: ![]()
|
Esempio |
||
|
Problema |
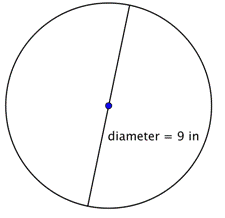
Trova la circonferenza del cerchio.
|
|
|
|
Per calcolare la circonferenza dato un diametro di 9 pollici, usa la formula Siccome stai usando un’approssimazione per |
|
|
Risposta |
La circonferenza è 9 |
|
|
Esempio |
||
|
Problema |
Trova la circonferenza di un cerchio con un raggio di 2. 5 iarde.5 iarde. |
|
|
|
Per calcolare la circonferenza di un cerchio dato un raggio di 2,5 iarde, usare la formula |
|
|
Risposta |
La circonferenza è 5 |
|
Un cerchio ha un raggio di 8 pollici. Qual è la sua circonferenza, arrotondata al pollice più vicino?
A) 25 pollici
B) 50 pollici
C) 64 pollici2
D) 201 pollici
L’area
![]() è un numero importante in geometria. L’hai già usato per calcolare la circonferenza di un cerchio. Si usa
è un numero importante in geometria. L’hai già usato per calcolare la circonferenza di un cerchio. Si usa ![]() anche quando si calcola l’area di un cerchio.
anche quando si calcola l’area di un cerchio.
Area di un cerchio
Per trovare l’area (A) di un cerchio, usa la formula: ![]()
|
Esempio |
||
|
Problema |
Trova l’area del cerchio.
|
|
|
|
Per trovare l’area di questo cerchio, usare la formula Ricordati di scrivere la risposta in termini di unità quadrate, dato che stai trovando l’area. |
|
|
Risposta |
L’area è 9 |
|
Un pulsante ha un diametro di 20 millimetri. Qual è l’area del bottone? Usa 3,14 come approssimazione di ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Figure composte
Ora che sai come calcolare la circonferenza e l’area di un cerchio, puoi usare questa conoscenza per trovare il perimetro e l’area di figure composte. Il trucco per risolvere questo tipo di problemi è identificare le forme (e le parti di forme) all’interno della figura composta, calcolare le loro dimensioni individuali, e poi sommarle.
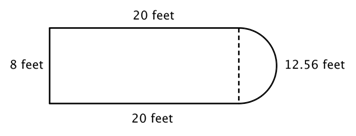
Per esempio, guarda l’immagine qui sotto. È possibile trovare il perimetro?
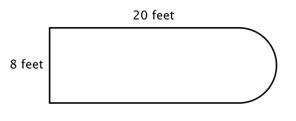
Il primo passo è identificare figure più semplici all’interno di questa figura composta. Puoi scomporla in un rettangolo e un semicerchio, come mostrato qui sotto.
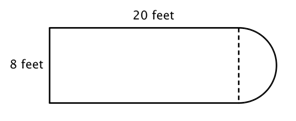
Sai come trovare il perimetro di un rettangolo e sai come trovare la circonferenza di un cerchio. Qui, il perimetro dei tre lati solidi del rettangolo è 8 + 20 + 20 = 48 piedi (nota che solo tre lati del rettangolo si aggiungono al perimetro della figura composta perché l’altro lato non è su un bordo; è coperto dal semicerchio!
Per trovare la circonferenza del semicerchio, usa la formula ![]() con un diametro di 8 piedi, poi prendi metà del risultato. La circonferenza del semicerchio è
con un diametro di 8 piedi, poi prendi metà del risultato. La circonferenza del semicerchio è ![]() , o circa 12,56 piedi, quindi il perimetro totale è circa 60,56 piedi.
, o circa 12,56 piedi, quindi il perimetro totale è circa 60,56 piedi.
|
Esempio |
||
|
Problema |
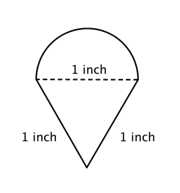
Trova il perimetro (al centesimo più vicino) della figura composta, formata da un semicerchio e un triangolo.
|
|
|
|
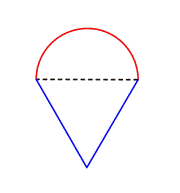
Identificare forme più piccole all’interno della figura composta. Questa figura contiene un semicerchio e un triangolo. |
|
|
Diametro (d) = 1
Circonferenza del semicerchio = |
Trova la circonferenza del cerchio. Poi dividere per 2 per trovare la circonferenza del semicerchio. |
|
|
|
|
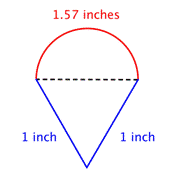
Trova il perimetro totale sommando la circonferenza del semicerchio e la lunghezza delle due gambe. Poiché la nostra misura della circonferenza del semicerchio è approssimativa, anche il perimetro sarà un’approssimazione. |
|
Risposta |
Approssimativamente 3.57 pollici |
|
|
Esempio |
||
|
Problema |
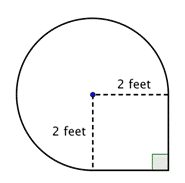
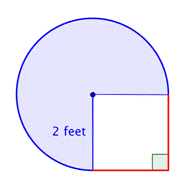
Trova l’area della figura composta, formata da tre quarti di cerchio e da un quadrato, al centesimo più vicino.
|
|
|
|
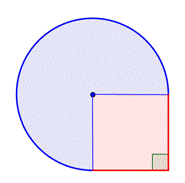
Identificare forme più piccole all’interno della figura composta. Questa figura contiene una regione circolare e un quadrato. Se trovi l’area di ciascuna, puoi trovare l’area dell’intera figura. |
|
|
|
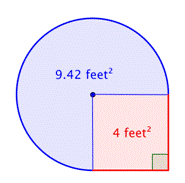
Trova l’area del quadrato. |
|
|
|
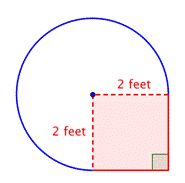
Nota che la regione è |
|
|
|
4 piedi2 + |
Aggiungete le due regioni. Poiché la tua misura dell’area circolare è approssimativa, anche l’area della figura sarà un’approssimazione. |
|
Risposta |
L’area è circa 13.42 piedi2. |
|
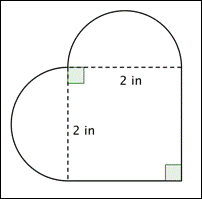
Qual è l’area (al centesimo più vicino) della figura mostrata sotto? (Entrambe le regioni arrotondate sono semicerchi.)
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3.14 in2
Sommario
I cerchi sono una forma geometrica importante. La distanza intorno a un cerchio è chiamata circonferenza, e lo spazio interno di un cerchio è chiamato area. Calcolare la circonferenza e l’area di un cerchio richiede un numero chiamato pi greco (![]() ), che è un decimale non terminante e non ripetitivo. Pi greco è spesso approssimato dai valori 3,14 e
), che è un decimale non terminante e non ripetitivo. Pi greco è spesso approssimato dai valori 3,14 e ![]() . È possibile trovare il perimetro o l’area di forme composte – comprese le forme che contengono sezioni circolari – applicando le formule della circonferenza e dell’area, dove appropriato.
. È possibile trovare il perimetro o l’area di forme composte – comprese le forme che contengono sezioni circolari – applicando le formule della circonferenza e dell’area, dove appropriato.