Nel consiglio del mese di novembre 2011 (TOTM) abbiamo presentato i calcoli del compressore di un caso studio. Abbiamo confrontato i risultati del metodo rigoroso con i valori dei metodi scorciatoia. Il metodo rigoroso era basato su un’equazione di stato come la Soave-Redlich-Kwong (SRK) per calcolare le entalpie e le entropie necessarie. Le entalpie e le entropie sono usate per determinare la richiesta di potenza e le temperature di scarico. I risultati hanno indicato che la precisione del metodo di scorciatoia è sensibile al valore del rapporto di capacità termica allo stato di gas ideale, k.
Dal solo punto di vista del calcolo, il calcolo della potenza è particolarmente sensibile alle specifiche della portata massica, della temperatura e della pressione di aspirazione e della temperatura e della pressione di scarico. Un compressore funzionerà sotto valori variabili delle variabili che influenzano le sue prestazioni. Quindi la parte più difficile del calcolo di un compressore è la specificazione di un intervallo ragionevole per ogni variabile e non il calcolo stesso. Reference sottolinea che usare un singolo valore per ogni variabile non è il modo corretto di valutare un sistema di compressione.
Normalmente, i calcoli termodinamici sono eseguiti per un processo ideale (reversibile). I risultati di un processo reversibile sono poi adattati al mondo reale attraverso l’uso di un’efficienza termodinamica. Nel processo di compressione ci sono tre processi ideali che possono essere visualizzati: 1) un processo isotermico (PV1=C1), 2) un processo isentropico (PVk=C2) e 3) un processo politropico (PVn=C3). Ognuno di questi processi può essere usato adeguatamente come base per valutare i requisiti di potenza di compressione sia con calcoli manuali che al computer. Il processo isotermico, tuttavia, è usato raramente come base perché il normale processo di compressione industriale non è nemmeno approssimativamente eseguito a temperatura costante.
Nota che Dresser Rand sta facendo un sacco di lavoro con la compressione a “temperatura quasi costante”, specialmente per la compressione di CO2 da camini di ventilazione. Per i dettagli riferirsi a:
In questo TOTM, dimostreremo come determinare l’efficienza di un compressore dalla portata misurata, composizione, temperature e pressioni di aspirazione e di scarico. Un calcolo rigoroso basato su un’equazione di stato e un metodo di scorciatoia sono considerati e i risultati sono confrontati.
Efficienza del compressore
Le efficienze dei compressori variano con il tipo di compressore, le dimensioni e la portata. Possono essere determinate solo (in seguito) da un test del compressore, anche se i produttori di compressori possono solitamente fornire buone stime. Per scopi di pianificazione, il riferimento suggerisce i seguenti valori per le efficienze complessive:
Tabella 1. Efficienze complessive del compressore
|
Tipo di compressore |
Efficienza, η |
|
Centrifugo |
0.70 – 0.85 |
|
Ripetizione ad alta velocità |
0.72 – 0.85 |
|
Ripetizione a bassa velocità |
0.75 – 0.90 |
|
Vite rotante |
0.65 – 0.75 |
Il riferimento indica che queste efficienze globali includono l’attrito del gas all’interno del compressore, le perdite meccaniche (cuscinetti, guarnizioni, cambio, ecc.), e le perdite del cambio. L’efficienza meccanica varia con le dimensioni e il tipo di compressore, ma il 95% è un numero di pianificazione utile. Quando si calcola la testa del compressore e la temperatura di scarico, l’efficienza utilizzata sarà isentropica o politropica (l’efficienza isentropica è talvolta chiamata efficienza adiabatica). Aggiungendo il 3-4 % di efficienza (perdite meccaniche) alle efficienze complessive della tabella 1 si ottiene generalmente una buona stima dell’efficienza termodinamica.
Per valutare le prestazioni di un compressore esistente, l’obiettivo è calcolare l’ficienza del compressore (η) e la richiesta di potenza.
Le proprietà note e misurate sono:
a. Portata volumetrica del gas in condizioni standard (qS) o portata massica del gas ()
b. Composizione del gas (zi)
c. Pressione di aspirazione (P1) e temperatura (T1)
d. Pressione di scarico (P2) e temperatura (T2)
Stima dell’efficienza – Metodo rigoroso
Il cuore di ogni software commerciale di simulazione del flusso di processo è un’equazione di stato. A causa della loro semplicità e relativa accuratezza, viene usata una EOS cubica come Soave Redlich-Kwong (SRK) o Peng-Robinson. Queste equazioni sono usate per calcolare gli equilibri vapore-liquido (VLE), l’entalpia (h) e l’entropia (s). Con adeguati coefficienti di interazione binaria, i risultati di simulazione del processo di queste due equazioni sono praticamente gli stessi. Pertanto, solo la SRK viene utilizzata in questo lavoro.
L’efficienza isentropica è definita da
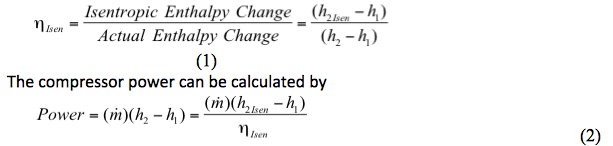
dove:
ηIsen = Efficienza isentropica
h1 = Entalpia di aspirazione calcolata a P1, T1, e composizione (zi)
h2 = Entalpia di scarico calcolata a P2, T2, e composizione (zi)
h2Isen = Entalpia di scarico isentropica a P2 (o T2), S2Isen =S1, e composizione (zi)
![]() = Portata massica
= Portata massica
Il calcolo dell’efficienza o potenza del compressore comporta due passi
1. Determinazione del cambiamento entalpico ideale o isentropico (reversibile e adiabatico) del processo di compressione (h2Isen-h1).
2. Determinazione del cambiamento entalpico reale (h2-h1).
Il calcolo passo dopo passo basato su un EOS:
a. Assumere lo stato stazionario, cioè
b. Supponiamo che la composizione dell’alimentazione rimanga invariata
c. Calcolare l’entalpia di aspirazione h1=f(P1, T1 e zi) e l’entropia s1=f(P1, T1 e zi) tramite EOS
d. Assumere un processo isentropico e impostare s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Calcolare l’entalpia ideale (h2Isen) alla condizione di scarico per zi noto, T2 (o P2) e s2Isen.
f. Calcolare l’entalpia reale (h2) alla condizione di scarico per zi, T2 e P2 noti.
g. Calcolare l’efficienza isentropica con l’equazione 1: µIsen = (h2Isen – h1)/(h2 – h1)
h. Calcolare la potenza con l’equazione 2: ![]()
Stimare l’efficienza – Metodo scorciatoia
L’esponente di percorso isentropico (k) o il rapporto di capacità termica del gas ideale (k=CP/CV) può essere calcolato con la correlazione presentata nel TOTM di maggio 2013:
![]()
dove:
T = Temperatura, K (°R)
![]() = Densità relativa del gas; rapporto tra peso molecolare del gas e peso molecolare dell’aria
= Densità relativa del gas; rapporto tra peso molecolare del gas e peso molecolare dell’aria
A = 0.000272 (0.000151)
La temperatura di scarico effettiva basata su un percorso isentropico può essere stimata da

Solvendo per l’efficienza isentropica,
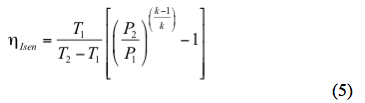
Similmente, la temperatura di scarico effettiva basata su un percorso politropico può essere stimata da

Solvendo l’equazione di cui sopra per il coefficiente di percorso politropico (n):

Similmente, la temperatura di scarico effettiva basata su un percorso politropico può essere stimata (ηPoly) da:

La prevalenza isentropica è calcolata da
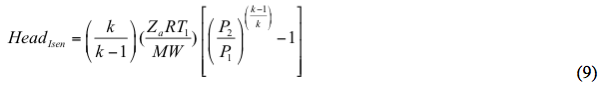
Similmente, la testa politropica è calcolata da
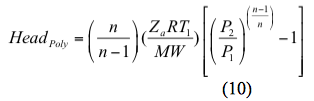
Per un processo isentropico (reversibile e adiabatico) la potenza è calcolata da
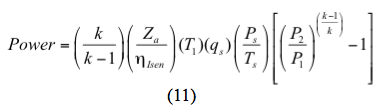
Oppure per un processo politropico la potenza è calcolata da
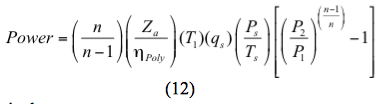
In alternativa:
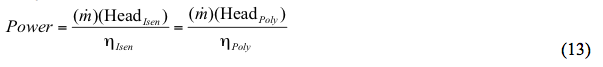
dove:
Head = Testa del compressore, m (ft)
Power = Potenza del compressore, kW (HP)
R = Costante universale del gas, 848 kg-m/(kmol-K) o (1545 ft-lbf/(lbmol-°R))
PS = Pressione delle condizioni standard, kPa (psia)
P1 = Pressione di aspirazione, kPa (psia)
P2 = Pressione di scarico, kPa (psia)
TS = Temperatura delle condizioni standard, K (°R)
T1 = Temperatura di aspirazione, K (°R)
T2 = Temperatura di scarico, K (°R)
qS = Tasso volumetrico del gas alla condizione standard, Sm3/d (scf/giorno)
Za = Fattore medio di compressibilità del gas = (Z1+Z2)/2
Z1 = Fattore di compressibilità del gas alla condizione di aspirazione
Z2 = Fattore di compressibilità del gas alla condizione di scarico
MW = Peso molecolare del gas
Il calcolo della potenza deve essere fatto per stadio di compressione e poi sommato per tutti gli stadi collegati ad un unico driver.
Il calcolo passo dopo passo per il metodo di scorciatoia
a. Calcolare l’esponente isentropico (k) con l’equazione 3 usando la temperatura media definita da T = (T1+3T2)/4. Questa forma di temperatura media è stata definita per ottenere una migliore corrispondenza tra i risultati del metodo rigoroso e quelli della scorciatoia.
b. Calcolare l’efficienza isentropica (ηIsen) con l’equazione 5.
c. Calcolare il coefficiente politropico (n) con l’equazione 7.
d. Calcolare l’efficienza politropica (ηPoly) con l’equazione 8.
e. Calcolare le teste isentropiche e politropiche con le equazioni 9 e 10, rispettivamente.
f. Calcolare la potenza richiesta per stadio con l’equazione 11 o 12.
Caso di studio
Una miscela di gas naturale viene compressa con un compressore centrifugo a tre stadi. Il diagramma di flusso del processo è mostrato nella figura 1. Per ogni stadio, la pressione misurata e la temperatura sono presentate nella tabella 1. La composizione dell’alimentazione misurata, le portate, il peso molecolare calcolato e la densità relativa sono presentati nella Tabella 2.
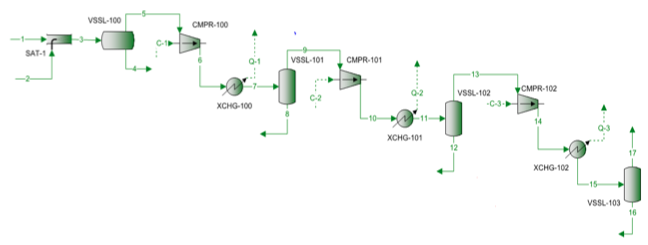
Figura 1. Diagramma di flusso del processo per una compressione a 3 stadi
Tabella 1. Temperatura e pressione misurate per i tre stadi di compressione
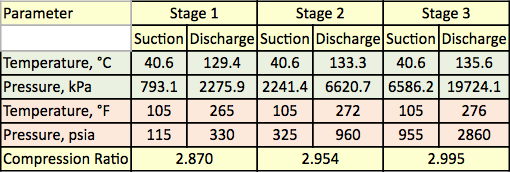
Tabella 2. Analisi del gas e portata per i tre stadi di compressione
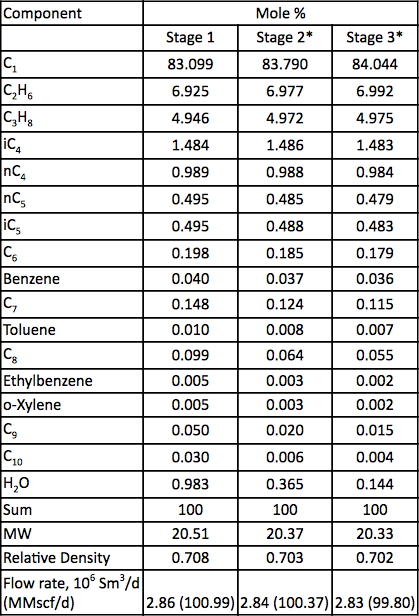
* Calcolato
Risultati e discussioni
Il diagramma di flusso del processo mostrato nella Figura 1 è stato simulato dal software ProMax per eseguire i calcoli rigorosi usando il SRK EOS. Il programma ha calcolato le efficienze politropiche e isentropiche, le teste e la potenza di compressione. Il programma ha anche calcolato l’esponente di percorso isentropico (k), e l’esponente di percorso politropico (n). Questi risultati calcolati sono presentati nella tabella 2 per tutti e tre gli stadi sotto le voci SRK. I calcoli eseguiti da ProMax sono molto simili al passo-passo di a attraverso h descritto nella sezione rigorosa. La tabella 2 presenta anche i risultati dei calcoli scorciatoia per i valori corrispondenti sotto la voce scorciatoia. I calcoli abbreviati sono basati sui passi da a a f descritti nella sezione del metodo abbreviato. Anche la percentuale di errore tra il metodo rigoroso e i metodi scorciatoia per ogni fase sono presentati nella tabella 2. La tabella 2 indica che si ottengono ottimi accordi per le fasi 1 e 2. Tuttavia, si osservano deviazioni maggiori per gli esponenti isetropici e politropici della fase 3 a causa del funzionamento ad alta pressione che si discosta troppo dalle condizioni di stato del gas ideale.
Tabella 3. Riassunto dei risultati calcolati rigorosi e scorciatoia
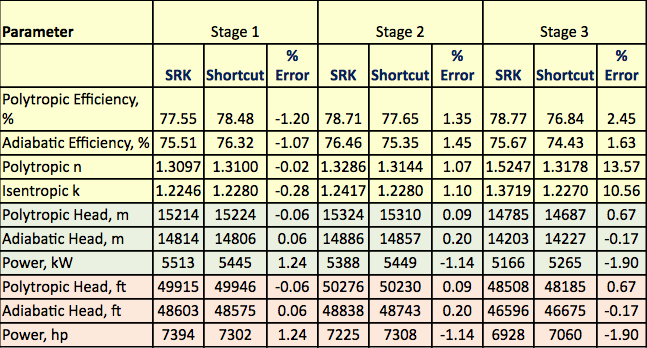
Conclusioni
La tabella 2 indica che ci sono buoni accordi tra i risultati rigorosi e scorciatoia. Le differenze tra i risultati del metodo rigoroso e della scorciatoia per i calcoli delle strutture e per la pianificazione sono trascurabili. Per la fase 3, a causa del funzionamento ad alta pressione e della deviazione eccessiva dalla condizione di stato di gas ideale, si osserva un errore maggiore per l’esponente isentropico (k).
L’esponente isentropico calcolato (k) nel ProMax non è il rapporto di capacità termica allo stato di gas ideale (CP/CV). È il valore dell’esponente isentropico che è richiesto per produrre un percorso isentropico dall’ingresso all’uscita. Il suo valore è calcolato come integrazione di quel percorso. Quindi è una specie di valore “medio” che rappresenta il vero percorso isentropico. Per i gas ideali, il valore sarebbe uguale al rapporto (CP/CV).
Questo errore in ‘k’ illustra anche l’importanza di specificare quale correlazione deve essere usata quando si ordina una prova di prestazione (cioè, fare riferimento a ASME PTC-10 per ulteriori dettagli), in modo che il cliente e il fornitore siano sullo stesso accordo per quanto riguarda il peso molecolare (MW) e k per il fluido della prova. Per ulteriori dettagli, fare riferimento ai TOTM di riferimento e di agosto e settembre 2010.
Può anche valere la pena notare che, quando si fa il trend di ‘n’ e dell’efficienza politropica per valutare le condizioni della macchina, la precisione relativa degli strumenti/apparecchiature di misurazione (trasduttori di temperatura e pressione) e la mappatura delle prestazioni del compressore alla curva originale delle prestazioni (portata effettiva del volume di gas rispetto alla velocità), introduce molte potenziali fonti erronee in questa valutazione quotidiana.
Nota che la precisione dei metodi di scorciatoia dipende dai valori di k e n. La definizione di temperatura media nel metodo di scorciatoia è stata regolata per ottenere una migliore corrispondenza tra l’esponente di percorso isentropico (k) calcolato con il metodo rigoroso.
Per saperne di più su casi simili e su come minimizzare i problemi operativi, suggeriamo di frequentare i nostri corsi G4 (Gas Conditioning and Processing), PF4 (Oil Production and Processing Facilities), ME46 (Compressor Systems-Mechanical Design and Specifications) e ME44 (Fundamentals of Pump and Compressors Systems).
PetroSkills offre consulenza su questo argomento e molti altri. Per ulteriori informazioni su questi servizi, visitate il nostro sito web all’indirizzo http://petroskills.com/consulting, o inviateci un’e-mail a [email protected].
Dr. Mahmood Moshfeghian
Riferimento:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., e Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, “Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J. “Aspetti importanti del test dei compressori centrifughi-Parte 1”, Suggerimento del mese, agosto 2010
8. Honeywell, J. “Aspetti importanti del test dei compressori centrifughi-Parte 2”, Suggerimento del mese, settembre 2010