Quella che segue è la mia presa su alcuni problemi di matematica di presunta “matematica Common Core” o “nuova matematica” che sono circolati su internet. Sento che ci mostrano un’implementazione sbagliata del CCS.

Tenete a mente che non tutto quello che vedete nei libri di matematica o su internet è fatto correttamente in base al CCS. In alcuni degli esempi che vedete, sembra che le persone stiano buttando via il buon senso quando fanno problemi di matematica per affrontare gli standard del Common Core!

Non sono sorpreso che l’implementazione sia finita “pasticciata” in alcuni posti. I CCS sono un tale cambiamento per la maggior parte degli insegnanti che hanno bisogno di un sacco di supporto e rieducazione prima di essere tenuti ad insegnare a loro.

Ho sempre pensato che il problema PRINCIPALE dell’educazione matematica nei gradi elementari nelle scuole pubbliche è che molti insegnanti elementari non capiscono la matematica a sufficienza per essere in grado di insegnarla correttamente anche a livello elementare. Per esempio, molti di loro non capiscono i concetti, i perché e i percome degli algoritmi che insegnano. Non è colpa loro – il problema risale a ciò che è stato insegnato loro nella formazione degli insegnanti e nella loro stessa formazione scolastica.

Anche lo stesso documento sugli standard è un po’ difficile da seguire in alcuni punti. Leggerlo richiede un po’ di riflessione. Vorrei che qualcuno producesse un opuscolo che spieghi gli standard in un linguaggio semplice e con numerosi esempi.

Cattivi esempi di “common core” o “nuova matematica”

Esempio 1

Di recente ho visto un’immagine di strategie di sottrazione su Facebook che sosteneva che era da un libro di matematica di 1° grado ed era “Common Core math.”

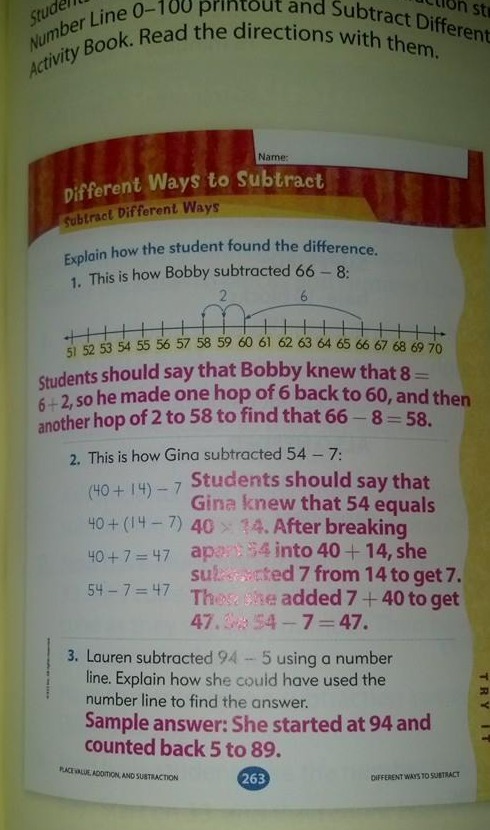
Penso che il metodo 2 sia troppo difficile per la prima elementare, e lascerei anche il metodo 1 per la seconda elementare.

Tuttavia, quel libro non sembra nemmeno allinearsi con gli standard Common Core. Gli standard per il 1° grado semplicemente non includono questo tipo di problemi di sottrazione!

Questo è ciò che troviamo negli standard:

Aggiungere e sottrarre entro 20.
1.OA.5
Relare il conteggio all’addizione e alla sottrazione (per esempio, contando su 2 per aggiungere 2).
1.OA.6.
Aggiungi e sottrai entro il 20, dimostrando scioltezza nell’addizione e sottrazione entro il 10. Usare strategie come contare su; fare dieci (ad esempio, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); scomporre un numero che porta ad una decina (ad esempio, 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); usare la relazione tra addizione e sottrazione (ad esempio, sapendo che 8 + 4 = 12, si sa che 12 – 8= 4); e creare somme equivalenti ma più facili o note (ad esempio aggiungere 6 +7 creando l’equivalente noto 6 + 6 + 1 = 12 + 1 = 13).

L’esempio del libro di testo sembra voler affrontare 1.OA.6 sopra, ma questo è chiaramente per l’addizione e la sottrazione entro il 20, non con numeri più grandi.

Più avanti negli standard di 1° grado vediamo due standard che hanno a che fare con la sottrazione di numeri a due cifre (entro 100):

1.NBT.5.
Dato un numero di due cifre, trovare mentalmente 10 più o 10 meno del numero, senza dover contare; spiegare il ragionamento usato.
1.NBT.6.
Sottrarre multipli di 10 nell’intervallo 10-90 da multipli di 10 nell’intervallo 10-90 (differenze positive o nulle), usando modelli concreti o disegni e strategie basate sul valore del luogo, le proprietà delle operazioni, e/o la relazione tra addizione e sottrazione; mettere in relazione la strategia con un metodo scritto e spiegare il ragionamento usato.
Nota di Maria: questo significa sottrazioni come 34 – 20 o 89 – 60.

ma nessuno di questi include sottrazioni come 54 – 7 o 82 – 6. Quelle sono in 2° grado:

2.NBT.5
Fluentemente aggiungere e sottrarre entro il 100 usando strategie basate sul valore di luogo, proprietà delle operazioni, e/o la relazione tra addizione e sottrazione.

Nota che lo standard di 2° grado non specifica COME si sottrae (se si usano strategie di matematica mentale o si scrivono i numeri uno sotto l’altro e si prendono in prestito/raggruppano).

Esempio 2

Da Houghton Mifflin, presumibilmente:

Juanita vuole dare borse di adesivi ai suoi amici. Vuole dare lo stesso numero di adesivi ad ogni amico. Non è sicura se ha bisogno di 4 borse o 6 borse di adesivi. Quanti adesivi può comprare in modo che non rimangano adesivi?

Il problema degli adesivi ha a che fare con il concetto di minimo comune multiplo (LCM). (La risposta è che dovrebbe comprare 12, 24, 36, o qualsiasi altro multiplo di 12 adesivi, perché così può dividerli in 4 sacchetti o 6 sacchetti)

Sicuramente, il problema è MOLTO poco chiaro e mal formulato. La mia ipotesi è che il libretto in cui questo appare sia semplicemente inedito. Non è colpa delle norme stesse. Sono d’accordo con Bart Goddard su Math Forum. Questo è un sintomo della corsa cieca a produrre problemi di storia “reali” che finiscono per essere insensibili.

Dal documento PDF in cui appare, concludo che il problema è per il quarto grado, perché tutti gli altri problemi di parole nel libretto corrispondono agli standard per il quarto grado (fattori, numeri primi). Ma i CCS non includono nemmeno il minimo comune multiplo negli standard di 4° grado (è nel 6°)! Qualcosa è andato davvero in tilt con quel problema di parole.

Esempio 3

Ancora una volta, presumibilmente da Houghton Mifflin per il 1° grado. Questo corrisponde allo standard che ho già citato sopra:

Aggiungere e sottrarre entro il 20.
1.OA.6.
Aggiungere e sottrarre entro il 20, dimostrando scioltezza nell’addizione e sottrazione entro il 10. Usare strategie come contare su; fare dieci (ad esempio, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); scomporre un numero che porta a un dieci (ad esempio, 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); usare la relazione tra addizione e sottrazione (ad es, sapendo che 8 + 4 = 12, si sa che 12 – 8 = 4); e creando somme equivalenti ma più facili o conosciute (per esempio, aggiungendo 6 + 7 creando l’equivalente noto 6 + 6 + 1 = 12 + 1 = 13).

Ora, prima di tutto, la strategia di “fare dieci” ha a che fare con l’ADDIZIONE, non con la sottrazione. Nella sottrazione, si chiama “scomporre un numero che porta a un dieci”. Quindi le istruzioni dovrebbero dire: “Quale mostra un modo di scomporre un numero che porta a un dieci?”. Credo che sia una totale ASSURDEzza richiedere agli studenti di prima elementare di conoscere tale terminologia.

Ma c’è un altro problema qui. Se leggete davvero tutti gli standard, noterete che in molti altri posti si chiede agli studenti di spiegare il ragionamento usato o di mettere in relazione un certo metodo visivo con la strategia, ma NON in questo standard!

Il modo in cui vedo questo standard è che gli insegnanti dovrebbero INSEGNARE le varie strategie menzionate e poi dare agli studenti semplici problemi di addizione e sottrazione entro il 20 come 15 – 8 e 10 – 6. NON vedo questo standard che richiede agli studenti di riconoscere se un certo modello visivo corrisponde a una certa strategia.

Ancora una volta, sembra che l’autore butti via il buon senso… e non capisca veramente gli standard.

Esempio 4

L’esempio qui sotto è formulato molto male ma il CONCETTO dietro è molto buono e si trova anche in Math Mammoth. Posso quindi capire cosa vogliono.

Vedi cinque quadrati. Colorane alcuni di blu e il resto di rosso. Questo è chiaro.

Poi colora i quadrati nel “legame numerico” allo stesso modo. Il legame numerico va a quei tre cerchi. Un bambino che è stato presente in una lezione in cui l’insegnante insegna i legami numerici si spera sappia cosa significa. È lo stesso concetto di una famiglia di fatti… il numero in alto è la somma o il totale (5), e i numeri che vanno ai cerchi in basso corrispondono a quanti ne hai colorati di blu e quanti di rosso, in questo caso 1 e 4.

Allora credo che i partner nascosti siano anche l’1 e il 4. Mostrate 1 e 4 dita ad un adulto. Infine colorare 1 e 4 dita nell’immagine (e non le proprie dita come sembra).

Secondo me la parte sulle dita è superflua e confusa. Tuttavia, il concetto di legami numerici è molto più vecchio del CCS. I legami numerici in realtà non sono menzionati nel CCS, anche se sono legati a questo standard:

1.OA.4
Comprendere la sottrazione come un problema di somma sconosciuta. Per esempio, sottrarre 10 – 8 trovando il numero che fa 10 quando viene aggiunto a 8.

e con questo

1.OA.6.
Aggiungi e sottrai entro il 20, dimostrando scioltezza per l’addizione e la sottrazione entro il 10.

Non so perché quel foglio di lavoro sui numeri sia dato come un esempio di Common Core Math. Sarebbe molto meglio intitolarlo come un esempio di foglio di lavoro di matematica mal formulato che potrebbe anche risalire a prima del Common Core (ed è solo riutilizzato in questo particolare curriculum)… perché come ho detto, i legami numerici NON sono menzionati nel CCS.

Cosa non sono i Common Core Math Standards

1. Non sono “nuova matematica”. Rispetto a molti curricula di matematica usati negli anni 2000 che enfatizzavano algoritmi non tradizionali, il CCS è un chiaro spostamento verso algoritmi tradizionali e memorizzazione. Guardate questi standard specifici:
   

   2.OA.2
   Fluentemente aggiungere e sottrarre entro il 20 usando strategie mentali. Entro la fine di Grade 2, conoscere a memoria tutte le somme di due numeri di una cifra.
   Nota di Maria: questi sono i fatti di addizione di base, come 7 + 7 o 5 + 4.

   3.OA.7
   Fluentemente moltiplicare e dividere entro il 100, usando strategie come la relazione tra moltiplicazione e divisione (per esempio, sapendo che 8 × 5 = 40, si sa che 40 ÷ 5 = 8) o proprietà delle operazioni. Entro la fine del Grade 3, conoscere a memoria tutti i prodotti di due numeri di una cifra.
   Nota di Maria: questo significa tabelle di moltiplicazione e fatti di divisione di base.

   4.NBT.4
   Aggiungi e sottrai fluentemente numeri interi a più cifre usando l’algoritmo standard.

   5.NBT.5
   Fluentemente moltiplica numeri interi a più cifre usando l’algoritmo standard.
   Nota di Maria: questo non significa che gli studenti moltiplicano numeri interi a più cifre solo in quinta classe; questo viene studiato anche in terza e quarta classe.

2. Gli standard non impongono strane strategie o modelli visivi a insegnanti e studenti. Molti standard lasciano la scelta agli insegnanti e agli studenti. Per esempio:
   

   2.NBT.5
   Aggiungi e sottrai con scioltezza entro il 100 usando strategie basate sul valore di luogo, sulle proprietà delle operazioni, e/o sulla relazione tra addizione e sottrazione.

   Nota il “e/o” nella frase sopra. Questo significa che gli insegnanti e gli studenti NON sono limitati all’uso di strategie specifiche né viene detto loro di usare diverse strategie. Il tradizionale algoritmo del “prestito” è una strategia basata sul valore di luogo, quindi è incluso proprio qui in 2.NBT.5.

   2.NBT.9
   Spiegare perché le strategie di addizione e sottrazione funzionano, usando il valore di luogo e le proprietà delle operazioni. Le spiegazioni possono essere supportate da disegni o oggetti.

   Dice “possono essere supportate da disegni” ma non vi obbliga a farlo, né vi limita ad usare uno specifico modello visivo o tipo di disegno.

   3.OA.3
   Utilizzare la moltiplicazione e la divisione entro il 100 per risolvere problemi di parole in situazioni che coinvolgono gruppi uguali, matrici e quantità di misura, per esempio, usando disegni ed equazioni con un simbolo per il numero sconosciuto per rappresentare il problema.

   Lo studente non DEVE usare un disegno.

   4.NBT.5
   Moltiplicare un numero intero fino a quattro cifre per un numero intero di una cifra e moltiplicare due numeri di due cifre, usando strategie basate sul valore di luogo e sulle proprietà delle operazioni. Illustrare e spiegare il calcolo utilizzando equazioni, matrici rettangolari, e/o modelli di aree.

   Nota il “e/o”. Illustrare il calcolo ma è sufficiente illustrarlo usando le equazioni. Non è NECESSARIO illustrarlo usando le matrici.

   Detto questo, alcuni standard menzionano un modello visivo specifico, come una linea numerica o un modello di area rettangolare, ma questo è meno comune che dare una scelta come negli standard sopra.

Matematica concettuale

Ci sono alcuni standard che entrano nel lato concettuale della matematica che gli insegnanti della scuola elementare potrebbero non capire se non viene loro insegnato cosa significano; per esempio:

5. NF.7b
Interpretare la divisione di un numero intero per una frazione unitaria e calcolare tali quozienti. Per esempio, creare un contesto di storia per 4 ÷ (1/5), e usare un modello visivo di frazione per mostrare il quoziente. Usare la relazione tra moltiplicazione e divisione per spiegare che 4 ÷ (1/5) = 20 perché 20 × (1/5) = 4.

Uno di questi problemi narrativi potrebbe essere: quanti pezzi lunghi 1/5 piedi si possono tagliare da un pezzo di materiale lungo 4 piedi? Un modello visivo potrebbe mostrare 4 parti intere, divise in quinte. Possiamo poi contare che 4 parti intere hanno un totale di 20 quinti.

5.NF.4b
Trovare l’area di un rettangolo con lati di lunghezza frazionaria piastrellandolo con quadrati unitari delle lunghezze dei lati della frazione appropriata, e dimostrare che l’area è la stessa che si troverebbe moltiplicando le lunghezze dei lati. Moltiplicare le lunghezze dei lati frazionari per trovare le aree dei rettangoli, e rappresentare i prodotti delle frazioni come aree rettangolari.

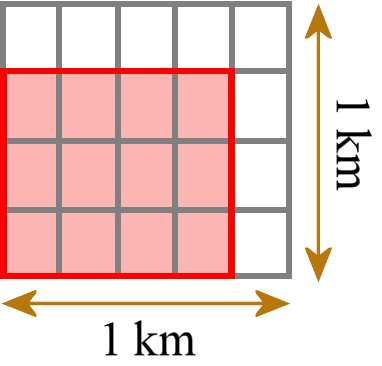Questo significa per esempio un rettangolo con lati di 3/4 km e 4/5 km. Poi lo piastrelliamo con piccoli rettangoli unitari (non quadrati unitari; qui lo standard stesso ha la terminologia sbagliata) che hanno ciascuno lato di 1/4 km e 1/5 km.

Possiamo contare di quante piccole piastrelle abbiamo bisogno. Abbiamo bisogno di 12 tessere di questo tipo. Ogni piastrella ha un’area di 1/20 km2, quindi l’area totale è 12/20 km2. Poi controlliamo e confrontiamo che otteniamo la stessa risposta come se avessimo moltiplicato le due lunghezze dei lati usando la normale moltiplicazione delle frazioni (3/4 km × 4/5 km = 12/20 km2).

Ho sempre avuto questo tipo di problemi nei miei libri – anche prima che arrivasse il CCS.

Alcuni sostengono che i bambini non hanno bisogno di questa comprensione concettuale o che è troppo difficile. Personalmente, non sono d’accordo. Ho sempre (anche prima del CCS) cercato di spiegare i concetti dell’aritmetica delle frazioni in modo che gli studenti non finiscano per “seguire ciecamente le regole”, capaci di calcolare con le frazioni solo se ricordano correttamente la regola. Ho sempre enfatizzato la comprensione concettuale in matematica (come i miei lettori sanno!).

Ma, spero che possiate vedere come alcune di queste cose possano essere poco familiari agli insegnanti e ai genitori, e quindi non c’è da meravigliarsi che seguire i Common Core Standards sia difficile per loro.

È mia speranza che Math Mammoth Light Blue Series e le unità che vendo nei miei negozi Teachers Pay Teachers e Teachers’ Notebook possano aiutare quegli insegnanti &genitori che hanno bisogno di materiali allineati al Common Core. E come ho detto, il resto di voi può essere sicuro di usarli pure. Non contengono nessuna matematica “strana” o insensata, ma come sempre, sono semplicemente basati sulla solida base di insegnare i concetti della matematica insieme alle procedure.

Di Maria Miller