Immagina un quadrato di carta disteso sulla tua scrivania. Vi chiedo di chiudere gli occhi. Sentite che la carta si sposta. Quando aprite gli occhi la carta non sembra essere cambiata. Cosa potrei avergli fatto mentre non stavi guardando?
È ovvio che non ho ruotato la carta di 30 gradi, perché allora la carta avrebbe un aspetto diverso.

Non l’ho nemmeno capovolta attraverso una linea che collega, diciamo, uno degli angoli al punto medio di un altro bordo. La carta avrebbe avuto un aspetto diverso se l’avessi fatto.

Quello che avrei potuto fare, comunque, era ruotare la carta in senso orario o antiorario di qualsiasi multiplo di 90 gradi, o capovolgerla attraverso una delle linee diagonali o le linee orizzontale e verticale.
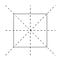
Un modo utile per visualizzare le trasformazioni è segnare gli angoli del quadrato.

L’ultima opzione è quella di non fare nulla. Questa è chiamata la trasformazione d’identità. Insieme, tutte queste sono chiamate trasformazioni di simmetria del quadrato.
Posso combinare le trasformazioni di simmetria per fare altre trasformazioni di simmetria. Per esempio, due capovolgimenti attraverso il segmento di linea BD producono l’identità, così come quattro rotazioni successive di 90 gradi in senso antiorario. Un capovolgimento sulla linea verticale seguito da un capovolgimento sulla linea orizzontale ha l’effetto sicuro di una rotazione di 180 gradi. In generale, qualsiasi combinazione di trasformazioni di simmetria produrrà una trasformazione di simmetria. La seguente tabella dà le regole per comporre le trasformazioni di simmetria:

In questa tabella, R con pedici 90, 180 e 270 denotano rotazioni in senso antiorario di 90, 180 e 270 gradi, H significa un capovolgimento intorno alla linea orizzontale, V è un capovolgimento intorno alla linea verticale, MD è un capovolgimento sulla diagonale dall’alto a sinistra al basso a destra, e OD significa un capovolgimento sull’altra diagonale. Per trovare il prodotto di A e B, vai alla riga di A e poi alla colonna di B. Per esempio, H∘MD=R₉₀.
Ci sono alcune cose che si possono notare guardando la tabella:
- L’operazione ∘ è associativa, cioè A∘(B∘C) = (A∘B)∘C per qualsiasi trasformazione A, B e C.
- Per ogni coppia di trasformazioni di simmetria A e B, anche la composizione A∘B è una trasformazione di simmetria
- C’è un elemento e tale che A∘e=e∘A per ogni A
- Per ogni trasformazione di simmetria A, esiste un’unica trasformazione di simmetria A-¹ tale che A∘A-¹=A-¹∘A=e
Diciamo quindi che l’insieme delle trasformazioni di simmetria di un quadrato, combinato con la composizione, forma una struttura matematica chiamata gruppo. Questo gruppo si chiama D₄, il gruppo diedro del quadrato. Queste strutture sono l’argomento di questo articolo.
Definizione di un gruppo
Un gruppo ⟨G,*⟩ è un insieme G con una regola * per combinare due elementi qualsiasi in G che soddisfa gli assiomi di gruppo:
In astratto spesso si sopprime * e si scrive a*b come ab e ci si riferisce a * come moltiplicazione.

Non è necessario che * sia commutativo, cioè che a*b=b*a. Lo si può vedere guardando la tabella di D₄, dove H∘MD=R₉₀ ma MD∘H=R₂₇₀. I gruppi in cui * è commutativo sono chiamati gruppi abeliani da Neils Abel.
I gruppi abeliani sono l’eccezione piuttosto che la regola. Un altro esempio di gruppo non abeliano sono le trasformazioni di simmetria di un cubo. Consideriamo solo le rotazioni intorno agli assi:
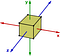
Se ruoto prima di 90 gradi in senso antiorario sull’asse y e poi di 90 gradi in senso antiorario sull’asse z, il suo risultato sarà diverso da quello che otterrei se ruotassi di 90 gradi sull’asse z e poi di 90 gradi sull’asse y.

È possibile che un elemento sia il suo inverso. Consideriamo il gruppo che consiste di 0 e 1 con l’operazione di addizione binaria. La sua tabella è:

E’ chiaro che 1 è il suo inverso. Anche questo è un gruppo abeliano. Non preoccupatevi, la maggior parte dei gruppi non sono così noiosi.
Alcuni altri esempi di gruppi includono:
- L’insieme dei numeri interi con addizione.
- L’insieme dei numeri razionali che non includono 0 con moltiplicazione.
- L’insieme delle soluzioni dell’equazione polinomiale xⁿ-1=0, chiamate radici ennesime di unità, con moltiplicazione.
Ecco alcuni esempi che non sono gruppi:
- L’insieme dei numeri naturali sotto addizione non è un gruppo perché non ci sono inversi, che sarebbero i numeri negativi.
- L’insieme di tutti i numeri razionali compreso 0 con moltiplicazione non è un gruppo perché non esiste un numero razionale q per cui 0/q=1, quindi non ogni elemento ha un inverso.
Struttura del gruppo
Un gruppo è molto più di un semplice blob che soddisfa i quattro assiomi. Un gruppo può avere una struttura interna, e questa struttura può essere molto intricata. Uno dei problemi di base dell’algebra astratta è determinare come appare la struttura interna di un gruppo, poiché nel mondo reale i gruppi che vengono effettivamente studiati sono molto più grandi e complicati dei semplici esempi che abbiamo dato qui.
Uno dei tipi fondamentali di struttura interna è un sottogruppo. Un gruppo G ha un sottogruppo H quando H è un sottoinsieme di G e:
- Per a,b∈H, a*b∈H e b*a∈H
- Per a∈H, a-¹∈H
- L’identità è un elemento di H
Se H≠G allora H è detto sottogruppo proprio. Il sottogruppo di G che consiste solo dell’identità è chiamato sottogruppo banale.
Un gruppo non abeliano può avere sottogruppi commutativi. Consideriamo il gruppo diedro quadrato che abbiamo discusso nell’introduzione. Questo gruppo non è abeliano ma il sottogruppo di rotazione è abeliano e ciclico:
Diamo ora due esempi di struttura di gruppo.
Anche se un gruppo G non è abeliano, può ancora accadere che ci sia un insieme di elementi di G che commutano con tutto in G. Questo insieme è chiamato centro di G. Il centro C è un sottogruppo di G. Prova:
Ora supponiamo che f sia una funzione il cui dominio e intervallo sono entrambi G. Un periodo di f è un elemento a∈G tale che f(x)=f(ax) per tutti x∈G. L’insieme P dei periodi di f è un sottogruppo di G. Prova:
I gruppi finiti sono generati finitamente
Abbiamo visto che i gruppi ciclici sono generati da un solo elemento. Quando è possibile scrivere ogni elemento di un gruppo G come prodotto di un sottoinsieme (non necessariamente proprio) A di G allora diciamo che A genera G e scriviamo questo come G=⟨A⟩. La prova più “beh, duh” che vedrai mai è la prova che tutti i gruppi finiti sono generati da un insieme generatore finito:
- Lascia che G sia finito. Ogni elemento di G è un prodotto di altri due elementi di G quindi G=⟨G⟩. QED.

Finiamo questo articolo con un’applicazione.
Comunicazione resistente agli errori
Il modo più semplice per trasmettere informazioni digitali è codificarle in stringhe binarie di lunghezza fissa. Nessuno schema di comunicazione è completamente libero da interferenze, quindi c’è sempre la possibilità che i dati sbagliati vengano ricevuti. Il metodo della decodifica a massima verosimiglianza è un approccio semplice ed efficace per individuare e correggere gli errori di trasmissione.
Lasciamo che 𝔹ⁿ sia l’insieme delle stringhe binarie, o parole, di lunghezza n. È facile dimostrare che 𝔹ⁿ è un gruppo abeliano sotto addizione binaria senza trasporto (così che per esempio 010+011=001). Si noti che ogni elemento è il suo inverso. Un codice C è un sottoinsieme di 𝔹ⁿ. Il seguente è un esempio di codice in 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Gli elementi di un codice sono chiamati codewords. Solo le parole in codice saranno trasmesse. Si dice che si verifica un errore quando un’interferenza cambia un bit in una parola trasmessa. La distanza d(a,b) tra due codici a e b è il numero di cifre in cui due codici differiscono. La distanza minima di un codice è la più piccola distanza tra due qualsiasi dei suoi codici. Per l’esempio di codice appena citato, la distanza minima è tre.
Nel metodo di decodifica a massima verosimiglianza, se riceviamo una parola x, che può contenere errori, il ricevitore dovrebbe interpretare x come la parola di codice a tale che d(a,x) sia un minimo. Mostrerò che per un codice di distanza minima m questo può sempre (1) rilevare errori che cambiano meno di m bit e (2) correggere errori che cambiano ½(m-1) o meno bit.

Nel nostro codice di esempio, m=3 e la sfera di raggio ½(m-1)=1 intorno alla parola chiave 011101 è {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Quindi, se il ricevitore riceve una qualsiasi di queste parole, sa che avrebbe dovuto ricevere 011101.
Quindi tutto questo va bene, ma cosa ha a che fare con la teoria dei gruppi? La risposta è nel modo in cui produciamo effettivamente i codici con cui questo metodo funziona.
È possibile che un codice in 𝔹ⁿ formi un sottogruppo. In questo caso diciamo che il codice è un codice di gruppo. I codici di gruppo sono gruppi finiti, quindi sono finitamente generati. Vedremo come produrre un codice trovando un insieme generatore.
Un codice può essere specificato in modo che i primi bit di ogni parola di codice sono chiamati bit di informazione e i bit alla fine sono chiamati bit di parità. Nel nostro esempio di codice C, i primi tre bit sono bit di informazione e gli ultimi tre sono bit di parità. I bit di parità soddisfano le equazioni di controllo di parità. Per un codice A₁A₂A₃A₄A₅A₆ le equazioni di parità sono A₄=A₁+A₂, A₅=A₂+A₃, e A₆=A₁+A₃. Le equazioni di parità forniscono un altro livello di protezione contro gli errori: se una qualsiasi delle equazioni di parità non è soddisfatta allora si è verificato un errore.
Ecco cosa facciamo. Supponiamo di volere delle parole chiave con m bit di informazione e n bit di parità. Per generare un codice di gruppo, scriviamo una matrice con m righe e m+n colonne. Nel blocco formato dalle prime m colonne, scrivete la matrice identità m×m. Nella colonna j per m+1≤j≤m_n, scrivere un 1 nella kesima riga se Aₖ appare nell’equazione di parità per il bit di parità Aⱼ e 0 altrimenti. Nel nostro codice di esempio, la matrice è:

Tale matrice è chiamata matrice generatrice del codice di gruppo. Si può verificare direttamente che le righe generano C:

Le righe di qualsiasi matrice generatrice formano un insieme generatore per un codice di gruppo C. Prova:
- Identità e inversi: Qualsiasi riga aggiunta a se stessa dà l’identità, una stringa composta da tutti zeri.
- Chiusura: Se A,B∈C allora A e B sono somme di righe della matrice generatrice quindi A+B è anche una somma di righe della matrice generatrice. Quindi A+B∈C.
Questo ci permette di generare un codice, ora mostrerò come generare un codice utile.
Definire il peso w(x) come il numero di uno in x. Per esempio, w(100101)=3. È ovvio che w(x)=d(x,0) dove 0 è una parola le cui cifre sono tutti zeri. Il peso minimo W di un codice è il peso della parola di codice non zero con il minor numero di uno nel codice. Per un codice di distanza minima m, d(x,0)≥m quindi w(x)≥m e quindi W=m.
Ricordiamo che perché una parola sia considerata un codeword, deve soddisfare un insieme di equazioni di controllo di parità. Per il nostro codice di esempio, queste sono A₄=A₁+A₂, A₅=A₂+A₃, e A₆=A₁+A₃. Possiamo anche scriverli come un sistema lineare:
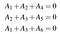
che può essere scritto in termini di prodotti punto:

O in forma più compatta come Ha=0 dove a=(A₁,A₂,A₃,A₄,A₅,A₆) e H è la matrice di controllo di parità del codice:

Si può verificare per calcolo diretto che se w(a)≤2 allora non possiamo avere Ha=0. In generale, il peso minimo è t+1 dove t è il numero più piccolo tale che qualsiasi insieme di t colonne di H non sommano a zero (cioè sono linearmente indipendenti). Dimostrare questo ci porterebbe un po’ troppo lontano nell’algebra lineare.
Se questo vi spaventa, non preoccupatevi. Possiamo produrre alcuni codici molto buoni senza di esso, approfittando del fatto che il risultato che ho appena menzionato implica che se ogni colonna di H non è zero e nessuna colonna è uguale, allora il peso minimo, e quindi la distanza minima del codice, è almeno tre. Questo è molto buono: se ci si aspetta che il nostro sistema di comunicazione abbia un errore di bit per ogni cento parole trasmesse, allora solo una su diecimila parole trasmesse avrà un errore non corretto e una su un milione di parole trasmesse avrà un errore non rilevato.
Ora abbiamo una ricetta per produrre un codice utile per lo schema di rilevamento della massima verosimiglianza per le parole in codice contenenti m bit di informazione e n bit di parità:
- Crea una matrice con m+n colonne e n righe. Riempite la matrice con gli uni e gli zeri in modo che non ci siano due colonne uguali e nessuna colonna sia composta solo da zeri.
- Ogni riga della matrice di controllo di parità risultante corrisponde a una delle equazioni del bit di parità. Scriveteli come un sistema di equazioni e risolvete in modo che ogni bit di parità sia scritto in termini di bit di informazione.
- Create una matrice con m+n colonne e m righe. Nel blocco formato dalle prime m colonne, scrivete la matrice d’identità m×m. Nella colonna j per m+1≤j≤m_n, scrivete un 1 nella kesima riga se Aₖ appare nell’equazione di parità per il bit di parità Aⱼ e 0 altrimenti.
- Le righe di questa matrice sono i generatori di un gruppo di codice con distanza minima almeno tre. Questo è il codice che useremo.
Come esempio, supponiamo che io abbia bisogno di un semplice codice di otto parole e che io abbia bisogno solo di qualche rilevamento di errore di base e non di correzione, quindi posso cavarmela con una distanza minima di due. Voglio tre bit di informazione e due bit di parità. Scrivo la seguente matrice di controllo di parità:
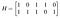
Ci sono due coppie di colonne che sono uguali, quindi il più piccolo t per cui qualsiasi insieme di t colonne è linearmente indipendente è uno, quindi il peso minimo, e quindi la distanza minima che avrò, è due. Le righe rappresentano le equazioni di controllo di parità A₄=A₁+A₃ e A₅=A₁+A₂+A₃. La mia matrice generatrice è dunque:

E le righe di questa matrice generano il gruppo di codici:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Riservazioni conclusive
L’algebra astratta è un argomento profondo con implicazioni di vasta portata, ma è anche molto facile da imparare. A parte qualche accenno di passaggio all’algebra lineare, quasi tutto quello che ho discusso qui è accessibile a qualcuno che ha avuto solo l’algebra del liceo.
Quando ho avuto l’idea di scrivere questo articolo volevo davvero parlare del cubo di Rubik, ma alla fine ho voluto scegliere un esempio che potesse essere trattato solo con le idee più basilari della teoria dei gruppi. Inoltre, c’è così tanto da dire sul gruppo del cubo di Rubik che merita un pezzo a sé stante, che arriverà presto.
I miei corsi universitari di algebra astratta erano basati sul libro A Book of Abstract Algebra di Charles Pinter, che è un trattamento accessibile. Gli esempi in questo articolo sono stati tutti presi in prestito con qualche modifica da Pinter.
Come nota finale, tutte le immagini che non sono citate sono il mio lavoro originale e possono essere usate con attribuzione. Come sempre, apprezzo qualsiasi correzione o richiesta di chiarimento.