L’identità di Eulero sembra sconcertante:
![]()
Emerge da una formula più generale:
![]()
Yowza — stiamo mettendo in relazione un esponente immaginario con seno e coseno! E in qualche modo inserendo pi greco si ottiene -1? Potrebbe mai essere intuitivo?
Non secondo il matematico del 1800 Benjamin Peirce:
È assolutamente paradossale; non possiamo capirlo, e non sappiamo cosa significa, ma lo abbiamo dimostrato, e quindi sappiamo che deve essere la verità.
Ah, questo atteggiamento mi fa ribollire il sangue! Le formule non sono incantesimi da memorizzare: dobbiamo, dobbiamo, dobbiamo trovare un’intuizione. Ecco la mia:
La formula di Eulero descrive due modi equivalenti di muoversi in un cerchio.
Tutto qui? Questa stupefacente equazione riguarda la rotazione? Sì — e possiamo capirla basandoci su alcune analogie:
- Partendo dal numero 1, vediamo la moltiplicazione come una trasformazione che cambia il numero: $1 \cdot e^{i \pi}$
- La crescita esponenziale regolare aumenta continuamente 1 di un certo tasso per un certo periodo di tempo; La crescita esponenziale immaginaria ruota continuamente 1 per un certo periodo di tempo
- Crescere per unità di tempo “pi” significa andare per pi radianti intorno ad un cerchio
- Quindi, $e^{i \pi}$ significa partire da 1 e ruotare pi (metà del cerchio) per arrivare a -1
Questa è la visione di alto livello, tuffiamoci nei dettagli. A proposito, se qualcuno cerca di impressionarti con $e^{i \pi} = -1$, chiedigli di i alla i-esima potenza. Se non riescono a pensarci bene, la formula di Eulero è ancora un incantesimo per loro.
Aggiornamento: Mentre scrivo, ho pensato che un video potrebbe aiutare a spiegare le idee più chiaramente:
Comprensione di cos(x) + i * sin(x)
Il segno di uguale è sovraccarico. A volte intendiamo “associare una cosa ad un’altra” (come x = 3) e altre intendiamo “queste due cose descrivono lo stesso concetto” (come $\sqrt{-1} = i$).
La formula di Eulero è quest’ultima: dà due formule che spiegano come muoversi in un cerchio. Se esaminiamo il moto circolare usando la trigonometria, e percorriamo x radianti:
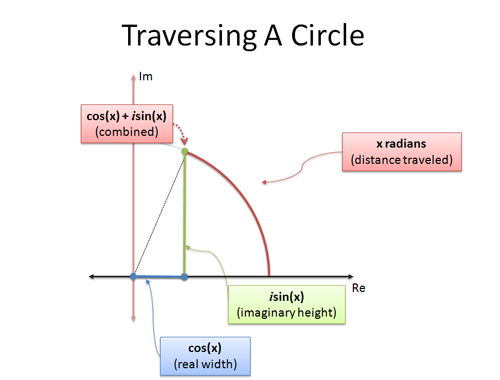
- cos(x) è la coordinata x (distanza orizzontale)
- sin(x) è la coordinata y (distanza verticale)
L’affermazione
![]()
è un modo intelligente per schiacciare le coordinate x e y in un unico numero. L’analogia “i numeri complessi sono bidimensionali” ci aiuta a interpretare un singolo numero complesso come una posizione su un cerchio.
Quando impostiamo x a $\pi$, stiamo viaggiando $\pi$ unità lungo l’esterno del cerchio unitario. Poiché la circonferenza totale è $2\pi$, il vecchio $\pi$ si trova a metà strada, mettendoci a -1.
Neato: Il lato destro della formula di Eulero ($\cos(x) + i \sin(x)$) descrive il moto circolare con numeri immaginari. Ora cerchiamo di capire come il lato e dell’equazione lo realizza.
Cos’è la crescita immaginaria?
Combinare le coordinate x e y in un numero complesso è difficile, ma gestibile. Ma cosa significa un esponente immaginario?
Facciamo un passo indietro. Quando vedo $3^4$, penso a questo:
- 3 è il risultato finale della crescita istantanea (usando e) ad un tasso di ln(3). In altre parole: $3 = e^{\ln(3)}$
- $3^4$ è lo stesso che crescere a 3, ma poi crescere per 4 volte più a lungo. Quindi $3^4 = e^{\ln(3) \cdot 4} = 81$
Invece di vedere i numeri da soli, puoi pensare a loro come a qualcosa a cui e doveva “crescere”. I numeri reali, come 3, danno un tasso di interesse di ln(3) = 1,1, e questo è ciò che e “raccoglie” mentre va avanti, crescendo continuamente.
La crescita regolare è semplice: continua a “spingere” un numero nella stessa direzione reale in cui stava andando. 3 × 3 spinge nella direzione originale, rendendolo 3 volte più grande (9).
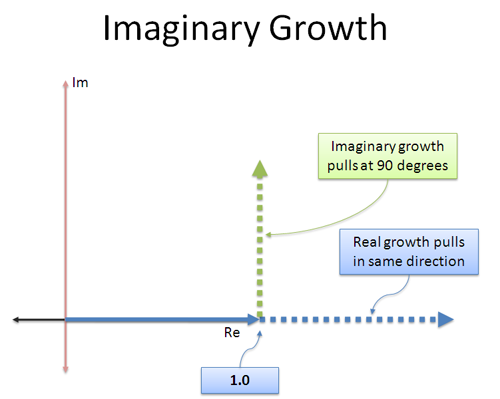
La crescita immaginaria è diversa: l'”interesse” che guadagniamo è in una direzione diversa! È come un motore a reazione che è stato attaccato lateralmente — invece di andare avanti, iniziamo a spingere a 90 gradi.
La cosa bella di una spinta ortogonale (perpendicolare) costante è che non ti fa accelerare o rallentare — ti fa ruotare! Prendendo qualsiasi numero e moltiplicandolo per i non cambierà la sua grandezza, ma solo la direzione in cui punta.
Intuitivamente, ecco come vedo il tasso di crescita immaginario continuo: “Quando cresco, non spingermi in avanti o indietro nella direzione in cui sto già andando. Fammi invece ruotare.”
Ma non dovremmo girare sempre più velocemente?
Me lo sono chiesto anch’io. La crescita regolare si compone nella nostra direzione originale, quindi andiamo 1, 2, 4, 8, 16, moltiplicando 2x ogni volta e rimanendo nei numeri reali. Possiamo considerare questo $e^{{ln(2)x}$, che significa crescere istantaneamente ad un tasso di ln(2) per “x” secondi.
E hey — se il nostro tasso di crescita fosse due volte più veloce, 2ln(2) vs ln(2), sembrerebbe lo stesso che crescere per il doppio del tempo (2x vs x). La magia di e ci permette di scambiare tasso e tempo; 2 secondi a ln(2) è la stessa crescita di 1 secondo a 2ln(2).
Ora, immaginiamo di avere un tasso di crescita puramente immaginario (Ri) che ci ruota fino a raggiungere i, o 90 gradi verso l’alto. Che cosa succede se raddoppiamo quel tasso a 2Ri, usciremo dal cerchio?
No! Avere una velocità di 2Ri significa che giriamo due volte più velocemente, o in alternativa, giriamo ad una velocità di R per il doppio del tempo, ma rimaniamo sul cerchio. Ruotare due volte più a lungo significa che ora siamo rivolti a 180 gradi.
Una volta che ci rendiamo conto che un certo tasso di crescita esponenziale può portarci da 1 a i, aumentare quel tasso ci fa solo girare di più. Non usciremo mai dal cerchio.
Tuttavia, se il nostro tasso di crescita è complesso (a+bi contro Ri) allora la parte reale (a) ci farà crescere come normale, mentre la parte immaginaria (bi) ci fa ruotare. Ma non esageriamo: La formula di Eulero, $e^{ix}$, riguarda la crescita puramente immaginaria che ci mantiene sul cerchio (più avanti).
Un rapido controllo di sanità mentale
Mentre scrivevo, ho dovuto chiarire alcune domande per me stesso:
Perché usare $e^x$, non stiamo ruotando il numero 1?
e rappresenta il processo di partire da 1 e crescere continuamente al 100% di interesse per 1 unità di tempo.
Quando scriviamo e stiamo catturando l’intero processo in un singolo numero — e rappresenta tutta la trafila della crescita continua. Quindi in realtà, $e^x$ sta dicendo “inizia da 1 e cresce continuamente al 100% per x secondi”, e parte da 1 come vogliamo.
Ma cosa fa i come esponente?
Per un esponente regolare come $3^4$ chiediamo:
- Qual è il tasso di crescita implicito? Stiamo crescendo da 1 a 3 (la base dell’esponente).
- Come cambiamo questo tasso di crescita? Lo scaliamo di 4x (la potenza dell’esponente).
Possiamo convertire la nostra crescita in formato “e”: il nostro tasso istantaneo è ln(3), e lo aumentiamo a ln(3) * 4. Di nuovo, la potenza dell’esponente (4) ha appena scalato il nostro tasso di crescita.
![]()
Quando l’esponente superiore è i (come in $3^i$), moltiplichiamo semplicemente il nostro tasso di crescita implicito per i. Quindi invece di crescere al vecchio ln(3), stiamo crescendo al ln(3) * i.
![]()
La parte superiore dell’esponente modifica il tasso di crescita implicito della parte inferiore.
I dettagli dettagliati
Diamo uno sguardo più da vicino. Ricordate questa definizione di e:
![]()
Che $\frac{100\%}{n}$ rappresenta la parte di interesse che abbiamo guadagnato in ogni periodo microscopico. Abbiamo assunto che il tasso di interesse fosse del 100% nella dimensione reale — ma se fosse del 100% nella direzione immaginaria?
![]()
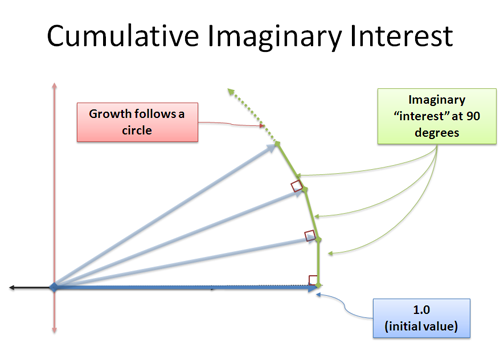
Ora, il nostro interesse appena formato ci aggiunge nella direzione dei 90 gradi. Sorprendentemente, questo non cambia la nostra lunghezza — questo è un concetto complicato, perché sembra fare un triangolo dove l’ipotenusa deve essere più grande. Abbiamo a che fare con un limite, e la distanza extra rientra nel margine di errore che specifichiamo. Questo è qualcosa che voglio affrontare un altro giorno, ma prendete la mia parola: la crescita perpendicolare continua vi ruoterà. Questo è il cuore di seno e coseno, dove il vostro cambiamento è perpendicolare alla vostra posizione attuale, e vi muovete in un cerchio.
Applichiamo i unità di crescita in incrementi infinitamente piccoli, ognuno dei quali ci spinge ad un angolo di 90 gradi. Non c’è una rotazione “sempre più veloce” – invece, strisciamo lungo il perimetro una distanza di |i| = 1 (grandezza di i).
E hey — la distanza strisciata intorno a un cerchio è un angolo in radianti! Abbiamo trovato un altro modo per descrivere il moto circolare!
Per ottenere il moto circolare: Cambiare continuamente ruotando a 90 gradi (alias tasso di crescita immaginario).
Quindi, la formula di Eulero sta dicendo “la crescita esponenziale e immaginaria traccia un cerchio”. E questo percorso è lo stesso che muoversi in un cerchio usando seno e coseno nel piano immaginario.
In questo caso, la parola “esponenziale” è confusa perché viaggiamo intorno al cerchio ad una velocità costante. Nella maggior parte delle discussioni, si suppone che la crescita esponenziale abbia un effetto cumulativo, composto.
Alcuni esempi
Non mi credete davvero, vero? Ecco alcuni esempi, e come pensarci intuitivamente.
Esempio: $e^i$
Dove è la x? Ah, è solo 1. Intuitivamente, senza tirare fuori una calcolatrice, sappiamo che questo significa “percorrere 1 raggio lungo il cerchio unitario”. Nella mia testa, vedo “e” che cerca di crescere di 1 al 100% tutto nella stessa direzione, ma i continua a muovere la palla e costringe “1” a crescere lungo il bordo di un cerchio:
![]()
Non è il numero più bello, ma è così. Ricorda di mettere la tua calcolatrice in modalità radianti quando lo inserisci.
Esempio: $3^i$
Questo è difficile – non è nel nostro formato standard. Ma ricordate, ![]()
Vogliamo una crescita iniziale di 3x alla fine del periodo, o un tasso istantaneo di ln(3). Ma, la i arriva e cambia quel tasso di ln(3) in “i * ln(3)”:
![]()
Pensavamo che avremmo trasformato ad un tasso regolare di ln(3), un po’ più veloce del 100% di crescita continua dato che e è circa 2,718. Ma oh no, ci ho fatto girare: ora ci stiamo trasformando ad un tasso immaginario che significa che stiamo solo ruotando. Se i fosse stato un numero regolare come 4, ci avrebbe fatto crescere 4 volte più velocemente. Ora stiamo crescendo ad una velocità di ln(3), ma lateralmente.
Dovremmo aspettarci un numero complesso sul cerchio dell’unità — non c’è nulla nel tasso di crescita per aumentare la nostra dimensione. Risolvendo l’equazione:
![]()
Così, invece di finire a “1” unità intorno al cerchio (come $e^i$) finiamo a ln(3) unità intorno.
Esempio: $i^i$
Alcuni mesi fa, questo mi avrebbe fatto piangere. Oggi no! Rompiamo le trasformazioni:
![]()
Partiamo da 1 e vogliamo cambiarlo. Come risolvere $3^i$, qual è il tasso di crescita istantaneo rappresentato da i come base?
Hrm. Normalmente faremmo ln(x) per ottenere il tasso di crescita necessario per raggiungere x alla fine di 1 unità di tempo. Ma per un tasso immaginario? Abbiamo bisogno di fare un noodling su questo.
Per iniziare con 1 e crescere fino a i dobbiamo iniziare a ruotare all’inizio. Quanto velocemente? Beh, dobbiamo ottenere 90 gradi (pi/2 radianti) in 1 unità di tempo. Quindi la nostra velocità è $i \frac{\pi}{2}$. Ricordate che la nostra velocità deve essere immaginaria perché stiamo ruotando, non crescendo! Il vecchio $frac{pi}{2}$ è circa 1,57 e risulta in una crescita regolare.
Questo dovrebbe avere senso: per trasformare 1,0 in i alla fine di 1 unità, dovremmo ruotare $frac{pi}{2}$ radianti (90 gradi) in quella quantità di tempo. Quindi, per ottenere “i” possiamo usare $e^{i \frac{\pi}{2}}$.
![]()
Phew. Questo descrive i come base. E l’esponente?
Bene, l’altro i ci dice di cambiare la nostra velocità – sì, quella velocità che abbiamo impiegato tanto tempo a capire! Quindi, piuttosto che ruotare ad una velocità di $i \frac{\pi}{2}$, che è ciò che significa una base di i, trasformiamo il tasso in:
![]()
Le i si annullano e rendono il tasso di crescita nuovamente reale! Abbiamo ruotato il nostro tasso e ci siamo spinti verso i numeri negativi. E un tasso di crescita negativo significa che ci stiamo restringendo — dovremmo aspettarci che $i^i$ renda le cose più piccole. E lo fa:
![]()
Tada! (Cerca “i^i” su Google per usare la sua calcolatrice)
Fai una pausa: Puoi capire intuitivamente come dovrebbero comportarsi le basi immaginarie e gli esponenti immaginari. Wow.
E come bonus, hai capito ln(i) — per far diventare i $e^x$, fai ruotare e di $frac{pi}{2}$ radianti.
![]()
Esempio: (i^i)^i
Un doppio esponente immaginario? Se insisti. Prima di tutto, sappiamo quale sarà il nostro tasso di crescita all’interno della parentesi:
![]()
Abbiamo un tasso di crescita negativo (restringente) di -pi/2. E ora modifichiamo di nuovo quel tasso per i:
![]()
E ora abbiamo una rotazione negativa! Stiamo girando intorno al cerchio ad una velocità di $-\frac{{pi}{2}$ per unità di tempo. Per quanto tempo andiamo avanti? Beh, c’è un’unità di tempo implicita “1” all’inizio di questa catena di esponenti; il default implicito è di andare per 1 unità di tempo (proprio come $e = e^1$). 1 unità di tempo ci dà una rotazione di $-\frac{{pi}{2}$ radianti (-90 gradi) o -i!
![]()
E, giusto per curiosità, se facciamo il quadrato di questo folle risultato:
![]()
È “solo” il doppio della rotazione: 2 è un numero regolare quindi raddoppia il nostro tasso di rotazione a ben -180 gradi in una unità di tempo. Oppure, puoi vederla come l’applicazione di una rotazione di -90 gradi due volte di seguito.
A prima vista, questi sono esponenti davvero strani. Ma con le nostre analogie possiamo prenderli in considerazione.
Crescita complessa
Possiamo avere crescita reale e immaginaria allo stesso tempo: la parte reale ci scala, e la parte immaginaria ci ruota intorno:
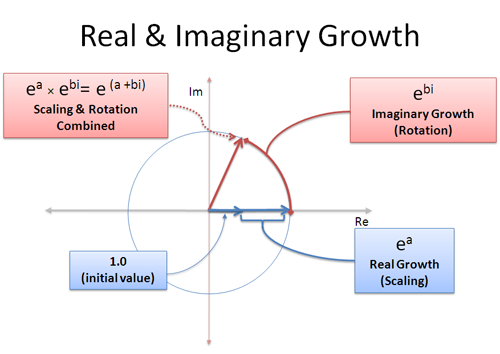
Un tasso di crescita complesso come (a + bi) è un mix di crescita reale e immaginaria. La parte reale a, significa “crescere al 100% per a secondi” e la parte immaginaria b significa “ruotare per b secondi”. Ricorda, le rotazioni non ottengono il beneficio della composizione poiché continui a “spingere” in una direzione diversa — la rotazione si somma linearmente.
Con questo in mente, possiamo rappresentare qualsiasi punto su qualsiasi cerchio di dimensioni usando (a+bi)! Il raggio è $e^a$ e l’angolo è determinato da $e^{bi}$. È come mettere il numero nell’expand-o-tron per due cicli: una volta per farlo crescere alla giusta dimensione (a secondi), un’altra volta per ruotarlo al giusto angolo (b secondi). Oppure, si potrebbe prima ruotarlo e poi farlo crescere!
Diciamo che vogliamo conoscere la quantità di crescita per arrivare a 6 + 8i. Questo è davvero chiedere il log naturale di un numero immaginario: come cresciamo e per ottenere (6 + 8i)?
- Radius: Quanto è grande il cerchio di cui abbiamo bisogno? Bene, la grandezza è $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Il che significa che abbiamo bisogno di crescere per ln(10) = 2,3 secondi per raggiungere quella quantità.
- Somma da ruotare: Qual è l’angolo di quel punto? Possiamo usare l’arctano per capirlo: atan(8/6) = 53 gradi = .93 radianti.
- Combina il risultato: ln(6+8i) = 2.3 + .93i
Quindi, possiamo raggiungere il punto casuale (6 + 8i) se usiamo $e^{2.3 + .93i}$.
Perché è utile?
La formula di Eulero ci dà un altro modo per descrivere il moto in un cerchio. Ma potremmo già farlo con seno e coseno — cosa c’è di così speciale?
È tutta una questione di prospettiva. Seno e coseno descrivono il moto in termini di una griglia, tracciando le coordinate orizzontali e verticali.

La formula di Eulero usa coordinate polari — qual è il tuo angolo e la tua distanza? Di nuovo, sono due modi di descrivere il moto:
- Sistema a griglia: Vai 3 unità verso est e 4 unità verso nord
- Coordinate polari: Vai a 5 unità con un angolo di 53,13 gradi
A seconda del problema, sono più utili le coordinate polari o rettangolari. La formula di Eulero ci permette di convertire tra le due per usare lo strumento migliore per il lavoro. Inoltre, poiché $e^{ix}$ può essere convertito in seno e coseno, possiamo riscrivere le formule di trigonometria come variazioni di e, il che è molto utile (non c’è bisogno di memorizzare sin(a+b), lo si può derivare — un altro giorno). Ed è bello che ogni numero, reale o complesso, sia una variazione di e.
Ma utilità, schmutility: il risultato più importante è la realizzazione che equazioni sconcertanti possono diventare intuitive con le giuste analogie. Non lasciate che le belle equazioni come la formula di Eulero rimangano un incantesimo – costruite sulle analogie che conoscete per vedere le intuizioni dentro l’equazione.
Felice matematica.
Appendice
Lo screencast è stato divertente, e il feedback è sicuramente benvenuto. Penso che aiuti a rendere le idee più brillanti, e camminare attraverso l’articolo mi ha aiutato a trovare lacune nella mia intuizione.
- Brian Slesinsky ha una bella presentazione sulla formula di Eulero
- Visual Complex Analysis ha una grande discussione sulla formula di Eulero — vedi p. 10 nella Google Book Preview
- Ho fatto un discorso su Math and Analogies che spiega più visivamente l’identità di Eulero:
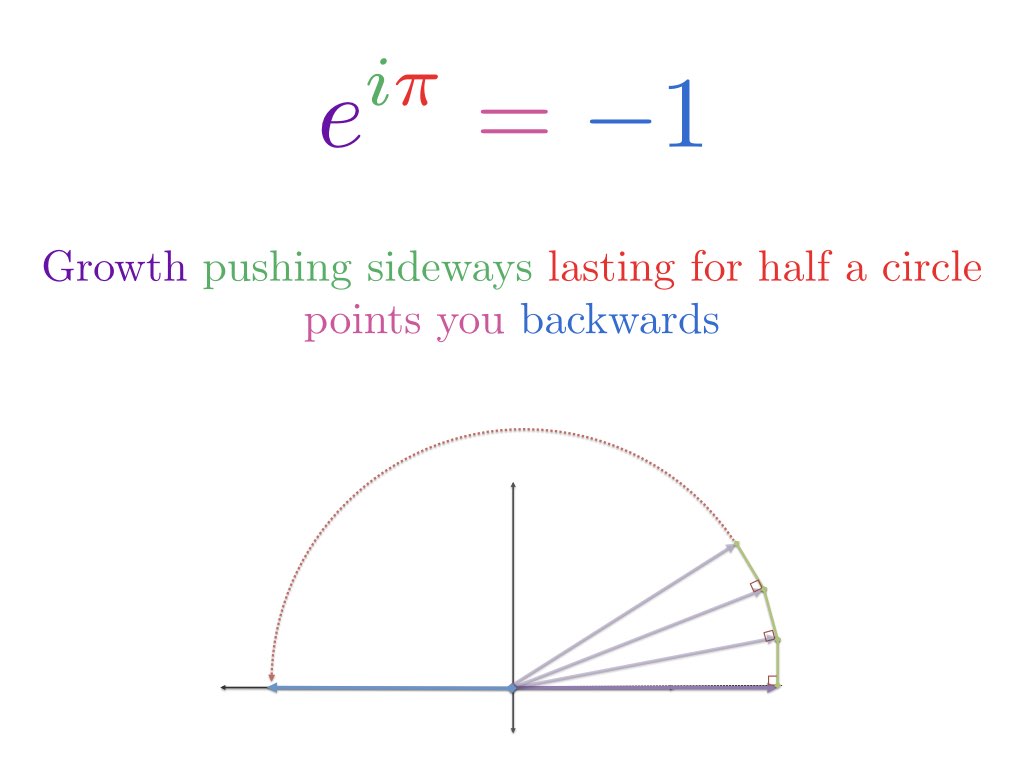
Altri post in questa serie
- Una guida visiva e intuitiva ai numeri immaginari
- Aritmetica intuitiva con numeri complessi
- Capire perché la moltiplicazione complessa funziona
- Guida intuitiva agli angoli, Gradi e radianti
- Comprensione intuitiva della formula di Eulero
- Guida interattiva alla trasformata di Fourier
- Guida intuitiva alla convoluzione
- Comprensione intuitiva delle onde sinusoidali
- Guida intuitiva all’algebra lineare
- Intuizione del programmatore per la moltiplicazione delle matrici
- Moltiplicazione immaginaria vs. Esponenti immaginari