Galileo is often considered Father of Modern Science.GALIEO は近代科学の父だと言われたことがある。 彼は、実験、理論、数学の原理を標準的な枠組みにまとめた人である。 5924>

ガリレオは、ピサの斜塔から質量は異なるが同じ材質の2つの鉄球を落とし、同時に着地させたという。 この実験で注目すべきは、仮説を検証するために実験を行うという、新しい科学の方法を切り開いたことです。

ガリレオはピサ大学の数学科の学科長だったときに、興味深いパラドックスを発見した。

定義。 パラドックスとは、アンチノミーとも呼ばれ、論理的に自己矛盾した文や、自分の予想に反する文のことである。 (ウィキペディア)。 (ギリシャ語：”para” = beyond, “doxa” = belief)

ガリレオのパラドックスとは、無限の対象を含む二つの集合が互いに等価であるかどうかを判断することであった。 例えば、Pを正の整数の集合でP={0,1,2,3,…}、Eを偶数の集合でE={0,2,4,6,…}としたとき、Pは偶数である。 ガリレオは、集合Pの各正整数と集合Eの偶数を対にできるので、この二つの集合の大きさは同じになると主張した。

では、Eに「少ない」数が現れると二つの集合の大きさは同じになるか? これはガリレオのパラドックスと呼ばれ、無限という概念について新しい議論が始まりました。

ガリレオの後、彼の弟子のエヴァンジェリスタ・トリチェリがピサ大学数学科の学科長になりました。 大気圧に関する研究や気圧計の発明などで、彼の名前を聞いたことがある人も多いだろう。 トリチェッリは数学にも興味を持っているので、

有限の体積と無限の表面をもつ物体は可能なのか、と問う。 そもそも、そのようなことはほとんどの人にとってあり得ないように思われます。 しかし、数学はそのようなことが起こりうることを教えてくれる。 トリチェリはその疑問に自ら答え、表面積は無限だが体積は有限である「トリチェリのトランペット」を発見した。 彼の発見は、「信じられない」パラドックスとみなされた。

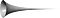
ところで数学哲学には「どの時代の哲学や数学でもその地域の歴史、文化、宗教と関係している」という本質的法則があるそうです。 だから、トリチェリのトランペットはガブリエルの角笛とも呼ばれているんだ。 ここで聖書に言及したのは、キリスト教では天使ガブリエルが審判の日に角笛を吹くと信じられているからです。

では、トリケッリのラッパはどのような形になるのでしょうか。 y=xのグラフの作り方は誰でも知っている。 代わりにxが1以上の方程式y=1/xをグラフにすると、次のようになります：

y=1/xのグラフをx軸の周りに回転させると、トリケッリのラッパが見えます。

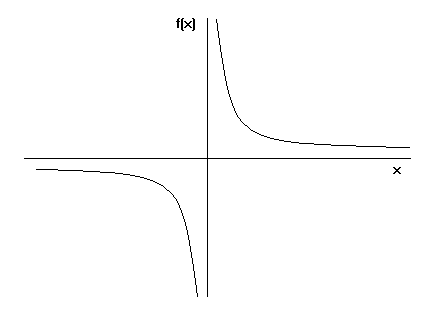
幸い、私たちの手にはトリケッリのラッパの面積と体積を算出できる数学式があるのですから。 トランペットの体積に下の積分式を使うと、有限になってしまいます。

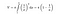
しかし、トランペットの表面積に積分式をかけると、今度は無限になってしまうのです。 この結果は面白いと思いませんか？

トリチェリのラッパの体積は有限なので、有限の量の絵具で満たすことができる。 たとえば、その体積を100リットルと仮定しよう。 ホームセンターに行って100リットルのペンキを買ってきて、それを入れる。 しかし、これが面白いのは、私はその100リットルの絵の具で無限の表面を塗ったことになることです。 今日、ほとんどの人はこのパラドックスを「画家のパラドックス」と呼んでいます。

Houston, we got a problem here! 実際には不可能な事態が数学では可能になる。 では、トリチェリのトランペットはどうすれば実在するのでしょうか？

これらの矛盾の原因は、無限という概念が私たちの知っている他の概念と似ていないことで、多くの人々を混乱させているからです。 ガリレオは自分のパラドックスについて、

「そうだ、私の友よ、無限はある。 それに反対するのは無駄なことだ。 私が取り組んでいる集合は、無限を含む閉じた集合の例です。 ある点から始まって無限に続くのですが、それでもなお集合なのです。 しかし、無限大に関する私のコメントや概念は、有限の大きさに対して使うものとは異なるはずです。 有限の大きさであれば、3キロは5キロより小さいとか、32メートルは7メートルより長いとか、そういう言い方ができる。 しかし、無限大になると、この無限大はこれより大きいとか小さいとか、これと等しいとは言えない」

これが1600年代のガリレオの解答であった。 数学者や哲学者は、カントールが今日の小学校で習う「集合論」を発表するまで、具体的な答えに合意することができなかったのです。

無限という概念の発展を定期的に歴史化することができます。 それはまず、紀元前5世紀初頭にパルメニデスが古代の町エレアに創設したソクラテス以前の哲学の一派であるエレア派から生まれたものである。 この学派には、ゼノン、クセノファネス、パルメニデスといった三大哲学者がいた。 この学派では、存在は単数であり、複数存在することはないという哲学が受け入れられていた。 ゼノンはエレア派での無限に関するパラドックスで有名である。 その後、紀元前300年代になると…, アリストテレスが現れ、ゼノンのパラドクスを説明するために、潜在的無限と現実的無限という一対の概念を提案した

潜在的無限とは、終点が認識できず、何度も何度も続くか繰り返される数群または「もの」の群れのことである。

実際の無限は、始まりと終わりがある空間内の終わらないセットや「もの」を含み、技術的には「完了」しているが無限のメンバーで構成されている系列である。 このアリストテレスの考え方は、1600年代まで哲学の世界を支配していた。 その後、クーサやブルーノなどの哲学者たちは、実際の無限は存在するが、それを理解することはできないと主張した。 クーサやブルーノのあとには、偉大な思想家スピノザがこの問題に参加した

スピノザは、私たちは無限という概念を理解し、その大きさをランク付けすることができると述べた。 しかし、それらについて計算することはできないとも述べている。

最後に、これらの議論を終わらせるために、ゲオルク・カントールという美しい男が現れ、現在でも数学の基礎となっている集合論を発見したのです。 彼は、無限集合が他の無限集合より大きくなったり小さくなったりすることを示し、無限議論に終止符を打ったのである。 さらにカントールは、無限集合の足し算や掛け算ができることを主張した。 それまでは、人間は無限大についてアリストテレスの考えに従っていた。 アリストテレスによれば、3という数字に無限大をかけると、また無限大になってしまう。 無限はすべてを飲み込んでしまうのだ。

しかし、カントールは集合論によって、アリストテレスの考えの逆を証明したのである。 無限の集合に1を加えると、それはもう同じ集合ではなくなる。 彼は無限集合を比較しようとした。 例えば、カントールは、(0,1)→ℕからのすべての関数の集合が可算であることを証明した。 つまり、0-1 の間には無限の有理数があり、これらの無限は対にできるので、0-1 の間にすべての自然数が収まることを証明したのである。 次に彼は、2つの等しい無限を見つけるよりもさらに危険なことをした。 彼は実数の無限と自然数の無限を比較して、実数の無限が他方より大きいことを発見したのです。 彼は自分の証明を見て、友人のデデキントに「私には見えるが、私でさえ信じられない・・・」とまで言った。

カントールはまた、非常に深刻な哲学的、宗教的関心を持つ数学者であった。 集合論を開発しながら、「神が私に集合論を指示した」と語っています。

集合論が開発された当初は、広く受け入れられるものではありませんでした。 企業はどんな仕事でもカントールを採用することはなかった。 数学者のポアンカレは、「このカントールの思想は、数学の襟元を刺す悪い病気だ」と言ったことがあります。 そして、数学はいつか彼を治療するだろう」と言った。 カントールは一時期、精神病院に入院し、そこで亡くなった。 しかし、今日、私たちは彼を天才だと考えています。

カントールは、無限の果てにいる孤独な男でした。 彼は「超限数」の論文の冒頭で聖書を引用しています。 “隠されているものはすべて明るみに出される”

。