以下は、インターネット上で出回っている「コモンコア数学」あるいは「新しい数学」とされるいくつかの数学の問題についての私の見解である。

数学の本やインターネットで目にするものすべてが、CCS に基づいて適切に行われているわけではないことを覚えておいてください。 あなたが見るいくつかの例では、コモンコア基準に対応するために数学の問題を作るときに、人々が常識を捨てているように見えます！

私は、いくつかの場所で実装が「失敗」に終わったことに驚いていません。 CCS はほとんどの教師にとって大きな変化であり、それに合わせて教えることを要求される前に、多くのサポートと再教育を必要とするのです。

私は常々、公立学校の小学校で算数教育が直面している最大の問題は、多くの小学校教師が、小学校レベルでも正しく教えることができるほど数学を理解していないことだと考えています。 例えば、多くの教師は、教えるアルゴリズムの概念や理由、原因を理解していません。 これは彼らのせいではありません。問題は、彼らが教員研修や自身の学校教育で教えられたことにさかのぼります。

標準文書自体も、ところどころでややわかりにくいところがあります。 それを読むには、少し考える必要があります。

「コモンコア」や「新しい数学」の悪い例

例1

最近、Facebookで、1年生の数学の本からのもので、「コモンコアの数学」と主張した引き算の戦略の画像を見た。「

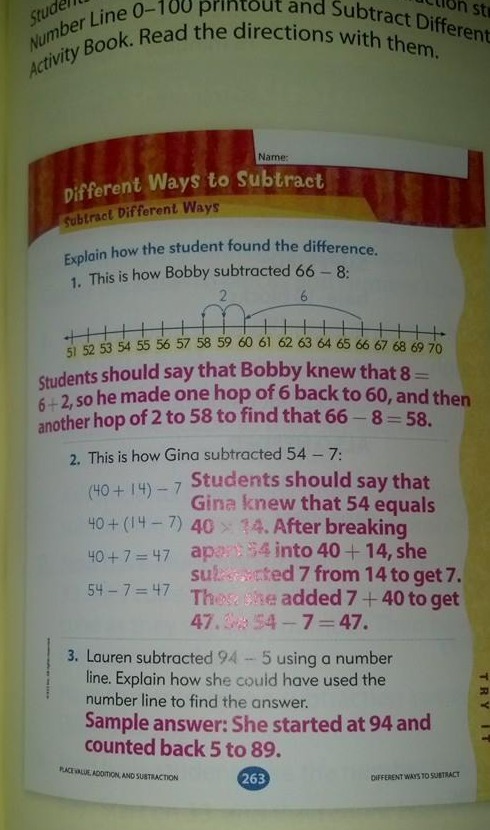
私は、方法 2 は 1 年生には難しすぎると思いますし、方法 1 でも 2 年生に任せます。

しかし、その本は Common Core 規格にさえ合っていないようです。 1年生の基準には、単にそのような引き算の問題は含まれていません！

基準にはこのように書かれています：

20以内の加減算
1.OA.5
足し算と引き算に関連付けることができる（例：2を足すために2で数える）
1.OA.6.
20以内の足し算と引き算、10以内の足し算と引き算に流暢に対応できることを示すことができる。 数え上げる、10を作る（例：8＋6＝8＋2＋4＝10＋4＝14）、10につながる数を分解する（例：13-4＝13-3-1＝10-1＝9）、足し算と引き算の関係を使う（例：8＋4＝12と知っていれば12-8＝4）、同等だが簡単な和や既知の和を作る（例：…など）といった手段を用いることができるようになります。

教科書の例では、上記の1.OA.6を取り上げたいようですが、これは明らかに20以内の足し算と引き算のためのもので、それ以上の数ではありません。

1年生の基準の後半では、2桁の数の引き算（100以内）に関係する基準が二つ出ています。）

1.NBT.5.
2桁の数が与えられたとき、数えることなく、その数より10多くまたは10少なくなるように計算し、その根拠を説明できる。.
10-90の範囲の10の倍数から10の倍数を引きます（差はプラスまたはゼロ）。具体的なモデルや絵を使い、場所の価値、演算の性質、および/または足し算と引き算の関係に基づいた戦略を使います。
マリアのメモ：これは34 – 20や89 – 60などの引き算を意味しています。

しかし、このどちらにも54 – 7や82 – 6のような引き算は含まれていません。 これらは2年生になります。

2.NBT.5
Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.

2年生の基準では、どのように引き算をするか（暗算の戦略を使うか、数字を互いに下に書いて借りたり組んだりするか）は指定されていないことに注意。

例2

Houghton Mifflinより、たぶん：

Juanita がステッカーの袋を友達にあげたいと言っています。 彼女はそれぞれの友だちに同じ数のステッカーをあげたいと考えています。 彼女は4袋か6袋のステッカーが必要かどうかわかりません。

ステッカーの問題は、最小公倍数（LCM）の概念に関係しています。 (答えは、12、24、36など、12の倍数のシールを買えば、4袋か6袋に分けられるからです。)

確かに、この問題は非常に不明瞭で言葉足らずなところがありますね。 私の推測では、これが掲載されている冊子は単に編集されていないだけだと思います。 規格自体のせいではありません。 私はMath ForumのBart Goddardに同意します。 これは、無意味に終わる「現実的な」ストーリー問題を作ろうとする盲目的なラッシュの症状なのです。

この問題が掲載されているPDF文書から、私はこの問題は4年生向けだと結論づけました。なぜなら、この冊子の他のすべての単語問題は4年生の基準（因子、素数）に合致しているからです。 しかし、CCSは最小公倍数を4年生の基準にさえ含めていません（6年生にあります）!

例題 3

これも Houghton Mifflin の 1 年生用と思われるものです。 これは、すでに上で引用した標準と一致します。

Add and subtract within 20.
1.OA.6.
Add and subtract within 20, demonstrate fluency for addition andsubtraction within 10.
Add and subtract within 20, demonstrate fluency for addition andsubtraction within 10. 数え上げる、10を作る（例：8＋6＝8＋2＋4＝10＋4＝14）、10につながる数を分解する（例：13-4＝13-3-1＝10-1＝9）、加減算の関係を利用する（例：…など）といった戦略を用いることができます。 8 + 4 = 12 と知っていれば、12 – 8 = 4 とわかる）、等価だが簡単な、あるいは既知の和を作る（例：既知の等価値 6 + 6 + 1 = 12 + 1 = 13 を作ることによって 6 + 7 を加える）

さてまず第一に、「10を作る」戦略は引き算ではなく足し算に関係するものである。 引き算では「10に至る数を分解する」といいます。 だから、説明書には、”10につながる数の分解方法を示すものはどれか “と書いてあるはずです。 このような専門用語を1年生に要求するのは全くナンセンスだと思います。

しかし、ここにも問題があります。 実際に基準をすべて読んでみると、他のいくつかの場所では、使用した理由を説明したり、特定の視覚的な方法を戦略に関連付けるよう生徒に求めているが、この基準にはないことに気づくだろう。

私が考えるに、この基準は、教師が言及されたさまざまな戦略を教え、その後、15-8や10-6など20以内の単純な加算や減算問題を与えることになっているのである。 私はこの基準が、ある視覚的モデルがある戦略に合致するかどうかを生徒が認識することを求めているとは思えません。

ここでも著者は常識を捨て…実際に基準を理解していないようです。

Example 4

以下の例は非常に下手な表現ですが、その背後にあるコンセプトは非常によく、Math Mammothにも掲載されています。

5つの正方形が見えます。 いくつかを青に、残りを赤に着色します。

次に「ナンバーボンド」のマスを同じように色付けします。 数字の絆はその3つの丸に通じる。 先生がナンバー・ボンドを教える授業に立ち会ったことのある子どもは、うまくいけばその意味を知っている。 ファクトファミリーと同じ考え方で、一番上の数字は合計（5）、一番下の丸に入る数字は、青を何個、赤を何個塗ったか、この場合1と4が対応しているんです。 1と4の指を大人に見せます。 最後に絵の中の1と4の指に色をつけます(聞こえるように自分の指ではありません)。

私見ですが、指に関する部分は超大変で、混乱すると思います。 しかし、ナンバーボンドのコンセプトはCCSよりずっと古いものです。

1.OA.4
Understanding subtraction as an unknown-addend problem（引き算を足し算の問題として理解する）。 例えば、8を足して10になる数を見つけることで、10-8を引きます。

また、

1.OA.6.
Add and subtract within 20, demonstency for addition andsubtraction within 10.

なぜあのナンバーボンドワークシートが、Common Core Mathの例としてあげられているのか分かりません。 コモン・コア以前から使われていた可能性のある（そしてこの特定のカリキュラムで再利用されている）、言葉足らずの算数ワークシートの例と題した方がずっといいでしょう。

What Common Core Math Standards are not

1. They are not “new math”. 2000年代に使われた多くの数学カリキュラムが、非伝統的なアルゴリズムを強調していたのと比べると、CCSは明らかに伝統的なアルゴリズムと暗記に向かうものです。 具体的な基準をご覧ください：
   

   2.OA.2
   Fluently add and subtract within 20 using mental strategies（20以内の足し算と引き算を暗算で行う）。 2年生の終わりまでに、1桁の数字2つの和をすべて記憶しておく。
   マリア注：7＋7や5＋4など、基本的な足し算の事実を指します。

   3.OA.7
   100以内の掛け算と割り算を、掛け算と割り算の関係（例えば、8×5＝40と知っていれば、40÷5＝8とわかる）や演算の性質などの戦略を使って、流暢に行うことができる。 第3学年の終わりには、1桁の数字2つの積をすべて記憶していること。

   4.NBT.4
   Fluently add and subtract multi-digit whole numbers using the standard algorithm.

   5.NBT.5
   Fluently multiply multi-digit whole numbers using the standard algorithm.
   Maria’s note: この意味は5年生だけでマルチ桁数の整数をかけるのではなく、3、4年生でも勉強していることである。

2. 標準は、奇妙な戦略や視覚的モデルを教師や生徒に押し付けるものではない。 多くの基準は教師や生徒にそれを委ねている。 例えば、
   

   2.NBT.5
   Fluently add and subtract within 100 using strategies based on placevalue, properties of operations, and/or the relationship betweenaddition and subtraction.

   上記の文章中の「および／または」に注目してください。 これは、先生や生徒が特定の戦略を使うことに制限されないし、いくつかの戦略を使うように言われないということです。 伝統的な「借り方」アルゴリズムは、場所値に基づく戦略なので、ここ2.NBT.5で含まれています。

   2.NBT.9
   加算と減算の方法がなぜ有効なのか、プレースバリューと操作の特性を用いて説明することができる。

   “may be supported by drawings “とありますが、それを強制するわけでもなく、特定の視覚モデルや図面のタイプを使用するように制限するわけでもないのです。
   Use multiplication and division within 100 to solve word problems insituations involving equal groups, arrays, and measurement quantities.ex.by using drawing and equations with a symbol for the unknownnumber to represent the problem.

   The student does not have to use a drawing. 生徒は、図面を使用しなければならないわけではありません。 6446>

   4.NBT.5
   4桁までの整数と1桁の整数との掛け算、および2桁の2つの数字の掛け算を、位取りと演算の性質に基づいた戦略で行うことができる。 方程式、直方体、および/または面体を使って計算を説明することができます。 計算を図示するが、方程式を使って図示すれば十分である。

   そうは言っても、いくつかの基準は、数直線や長方形の面積モデルなど、特定の視覚的なモデルに言及していますが、それは上記の基準のように選択肢を与えることよりも一般的ではありません。

Conceptual math

小学校の教師がその意味を教えられないと理解できないかもしれない、数学の概念的な面に踏み込んだ標準がいくつかあります：たとえば、

5. NF.7b
整数の単位分数による除算を解釈し、そのような商を計算することができる。 例えば，4 ÷ (1/5)の文脈を作り，商を示すために視覚的な分数モデルを使用する。 掛け算と割り算の関係を利用して、20×（1/5）＝4なので、4÷（1/5）＝20と説明する。

このような話の問題の1つは、4フィートの材料から1/5フィートの長さの部分をいくつ切り出せるか？ 視覚的なモデルとして、5分の1に分割された4つの穴を示すことができます。

5.NF.4b
分数の辺の長さを持つ長方形を、適切な単位分数の辺の長さを持つ単位正方形で並べ、その面積が辺の長さを掛け合わせたものと同じであることを示すことによって、その面積を求めることができる。 分数の辺の長さを掛けて長方形の面積を求め、分数の積を長方形の面積として表す

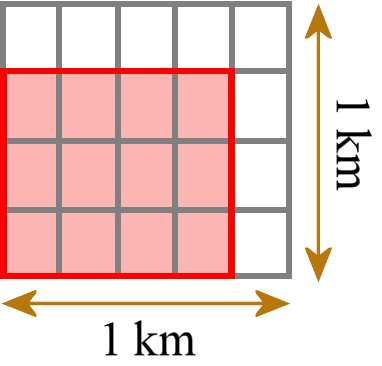これは、例えば辺の長さが3/4kmと4/5kmの長方形を意味します。

私たちは、いくつの小さなタイルが必要かを数えることができます。 このようなタイルが12個必要である。 それぞれのタイルの面積は1/20 km2なので、全体の面積は12/20 km2です。 そして、2つの辺の長さを通常の分数の掛け算で求めたのと同じ答え（3/4 km × 4/5 km = 12/20 km2）になることを確認し比較します。

私は、CCSが登場する以前から、この種の問題をいつも本で扱ってきました。 個人的には、そうは思いません。 私はいつも（CCS以前も）、生徒が「盲目的に規則に従う」ことにならないように、また、たまたま規則を正しく覚えていた場合にのみ分数で計算できるように、分数の算術の概念を説明することに努めてきました。 私は常に、数学における概念的な理解を重視しています（読者の皆さんはご存じでしょう！）。

しかし、これらの中には、学校の先生や保護者にとって馴染みのないものもあり、したがって、コモンコアスタンダードに従うことが難しいのも当然だということがお分かりいただけると幸いです。

私がTeachers Pay TeachersやTeachers’ Notebookの店舗で販売しているMath Mammoth Light Blueシリーズやユニットが、コモンコア準拠の教材を必要とする先生&や保護者の方のお役に立てれば幸いです。 そして、私が言ったように、他の皆さんも自信を持って使うことができるのです。 この教材には、「奇妙な」数学も無意味な数学も含まれていませんが、いつものように、数学の概念を手順とともに教えるという確かな基礎に基づいているだけです。

By Maria Miller