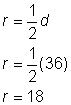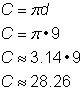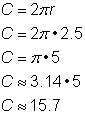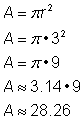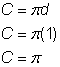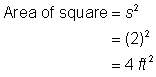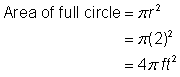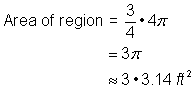円
学習目標
– 円の性質を識別する。
– 円の面積を求める。
– 複合幾何学図形の面積と周囲を求める。
はじめに
円はよく見られる形である。 車の車輪、空中を通過するフリスビー、データを転送するコンパクトディスクなど、いたるところで見かけます。
円は多角形や四角形と同じように2次元の図形です。 しかし、円は他の図形とは測り方が違いますし、表現する言葉も違います。
円の性質
円は、固定された中心点から同じ距離だけ離れた点の集合を表します。 この固定点を中心と呼ぶ。 円の中心から円上の任意の点までの距離を半径と呼ぶ。
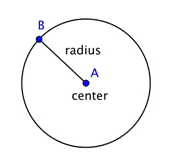
二つの半径(radiusの複数形)を合わせて円を横切る線分を作ると、直径となる。 円の直径は円の中心を通り、円周上に端点を持つ。
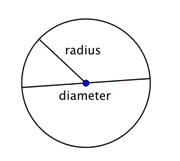
任意の円の直径は、その円の半径の長さの2倍である。 これは2r、つまり “半径の2倍 “という式で表すことができます。 つまり、円の半径がわかっていれば、それを2倍して直径を求めることができます。これはまた、円の直径がわかっていれば、2で割って半径を求めることができるということです。
|
例題 |
||
|
問題 |
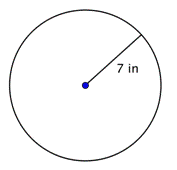
円の直径を求めてください。
|
|
|
d = 2r d = 2(7) d = 14 |
半径の2倍、2rで直径となる。 この円の半径は7インチなので、直径は2(7)=14インチです。 |
|
|
解答 |
直径は14インチです。 |
|
|
例題 |
||
|
問題 |
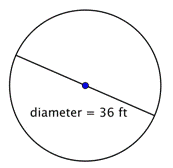
円の半径を求めよ。
|
|
|
|
半径は直径の半分、すなわち |
|
|
解答 |
半径は18フィートです。 |
|
円周
円の周りの距離を円周と呼びます。 (多角形の周りの距離は外周であることを思い出してください。)
円についての興味深い性質は、円の外周とその直径の比がすべての円で同じであることです。 円の大きさに関係なく、円周と直径の比は同じになります。
以下に、いろいろな物の実測値を示します。 寸法はミリメートルまたは1/4インチ(使用する測定単位によって異なる)単位で正確です。 それぞれ円周と直径の比率を見てください。アイテムは違いますが、比率はほぼ同じです。
|
アイテム |
円周(C)(小数第2位を四捨五入) |
比率 |
|
|
カップ |
253mm となります。 |
79 mm |
|
|
Quarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
外周と直径は正確に測定する方法がないため、概算の寸法です。 しかし、もし、もっと正確に測ることができれば、比![]() は、与えられた各項目について、3.14の方向に動くことがわかるでしょう。 比率
は、与えられた各項目について、3.14の方向に動くことがわかるでしょう。 比率![]() の数学的名称はπで、ギリシャ文字
の数学的名称はπで、ギリシャ文字![]() で表されます。
で表されます。
![]() は終端がなく、繰り返しのない10進数なので、完全に書き出すことは不可能です。
は終端がなく、繰り返しのない10進数なので、完全に書き出すことは不可能です。 ![]() の最初の10桁は3.141592653で、四捨五入して3.14としたり、分数
の最初の10桁は3.141592653で、四捨五入して3.14としたり、分数![]() として見積もったりすることが多いようです。 3.14も
として見積もったりすることが多いようです。 3.14も![]() も
も![]() の近似値で、正確さを求めない計算で使われることに注意。
の近似値で、正確さを求めない計算で使われることに注意。
円周と直径の比(![]() )はすべての円について一定なので、円の直径さえわかればこの数字で円周を求めることができる。
)はすべての円について一定なので、円の直径さえわかればこの数字で円周を求めることができる。
![]() =
= ![]() ですから、C =
ですから、C = ![]() d
d
また、d = 2rですから、C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r となります。
r となります。
円の円周
円の円周(C)を求めるには、次の公式のいずれかを用いる。 ![]()
円の半径(r)がわかっている場合。 ![]()
|
例題 |
||
|
問題 |
円の周囲を求めよ。
|
|
|
|
直径9インチから円周を計算するには
|
|
|
答え |
円周は9 |
|
|
例題 |
||
|
問題 |
半径が2インチの円の周長を求めよ。 |
|
|
|
半径2.5ヤードの円の円周は、 |
|
|
答え |
円周は5 |
|
ある円には8インチの直径がある。 円周は何インチになるか?
A) 25インチ
B) 50インチ
C) 64 inches2
D) 201 inches
面積
![]() は幾何学で重要な数字です。 円の円周を計算するときにすでに使いましたね。 円の面積を求めるときにも
は幾何学で重要な数字です。 円の円周を計算するときにすでに使いましたね。 円の面積を求めるときにも![]() を使います。
を使います。
円の面積
円の面積(A)を求めるには、次の公式を用います。 ![]()
|
例題 |
||
|
問題 |
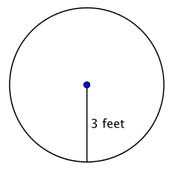
円の面積を求めよ。
|
|
|
|
この円の面積は |
|
|
答え |
面積は9 |
|
<5123>直径20ミリのボタンがあります。 このボタンの面積はいくらか。 ![]() .
.
A) 62.8 mm
B) 314 mm2
C) の近似値として3.14を使用します。 400 mm2
D) 1256 mm2
合成図形
円の外周と面積の計算方法がわかったので、この知識を使って合成図形の外周と面積を求めるとよいでしょう。 このような問題を解くコツは、合成図形の中にある図形(や図形の一部)を特定し、それぞれの寸法を計算し、それらを足し合わせることです。 周囲を求めることは可能でしょうか。
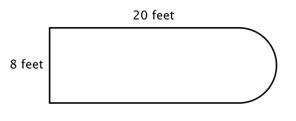
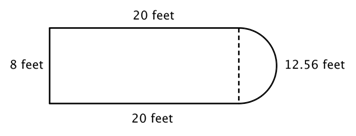
最初のステップは、この合成図形の中でより単純な図形を特定することです。 下図のように長方形と半円に分解できます。
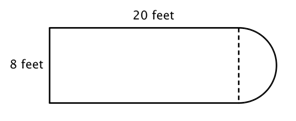
長方形の周囲を求める方法と、円の円周を求める方法は知っていると思います。 ここで、長方形の3つの実辺の周囲は8+20+20=48フィートです(長方形の3つの辺だけが合成図形の周囲に加わることに注意してください。 残りの辺は端ではなく、半円に覆われているからです!)
半円の周囲を求めるには、直径8フィートとして式 ![]() を使い、結果の半分を取りましょう。 半円の円周は
を使い、結果の半分を取りましょう。 半円の円周は![]() 、つまり約12.56フィートなので、全周囲は約60.56フィートとなる。
、つまり約12.56フィートなので、全周囲は約60.56フィートとなる。
|
例題 |
||
|
問題 |
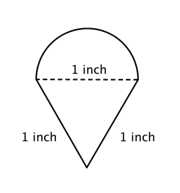
半円と三角の合成図形について周囲(100分位まで)求めよ。 |
|
|
|
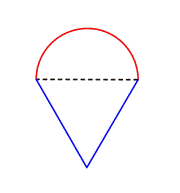
その図形から小さい図形を特定すること。 この図形は半円と三角形を含んでいる。 |
|
|
直径(d)=1
半円の円周= |
円の円周を求めます。 |
|
|
|
|
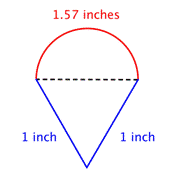
半円周と二つの足の長さを合わせて全周を求めます。 半円の円周は近似値なので、周囲も近似値になります。 |
|
答え |
約3.57インチ |
|
|
例題 |
||
|
問題 |
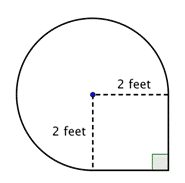
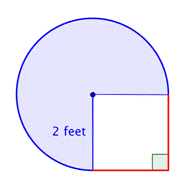
合成図の領域を求めよ。 円と正方形の4分の3を組み合わせたもので、100分の1に近い値です。
|
|
|
|
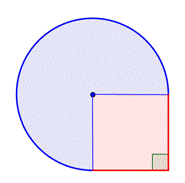
合成図形内の小さい図形を特定する。 この図形には、円形の領域と正方形が含まれています。 それぞれの面積を求めれば、図形全体の面積がわかります。 |
|
|
|
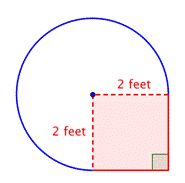
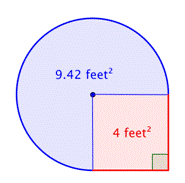
正方形の面積を求めて下さい。 |
|
|
|
|
円の領域の領域を求めよ。 半径は2フィートです。 領域は円全体の |
|
|
4 feet2 + |
|
|
答え |
面積は約13.42フィートです。42 feet2. |
|
下の図の面積(100分の1位まで)は何cmですか。 (丸めた部分はいずれも半円です。)
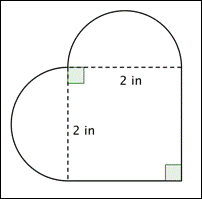
A) 16.56 in2
B) 7.14 in2
C) 4 in2
D) 3.14 in2
まとめ
円は重要な幾何図形である。 円の周りの距離を円周といい、円の内部の空間を面積といいます。 円の円周と面積を計算するには、π(![]() )という終端がなく、繰り返しのない10進数の数字が必要である。 円周率は、3.14や
)という終端がなく、繰り返しのない10進数の数字が必要である。 円周率は、3.14や![]() という値で近似されることが多い。 円形断面を含む複合図形の外周や面積は、円周率や面積の公式を適宜適用して求めることができる
という値で近似されることが多い。 円形断面を含む複合図形の外周や面積は、円周率や面積の公式を適宜適用して求めることができる
。