固有値は、連立方程式に関連するスカラーの特別なセット（すなわち、.e.,

システムの固有値および固有ベクトルの決定は、物理学および工学において非常に重要であり、それは行列対角化と同等であり、安定性解析、回転体の物理、および振動システムの小振動など、ごく一部の例を挙げると一般的なアプリケーションで発生する。 各固有値は対応するいわゆる固有ベクトルと対になっている（一般に、対応する右固有ベクトルと対応する左固有ベクトルがあり、固有値にはこれに類する左右の区別は存在しない）。

正方行列を固有値と固有ベクトルに分解することをこの作業では固有分解と呼び、の固有ベクトルからなる行列が正方である限りこの分解が常に可能であることを固有分解定理と呼ぶ。

ランチョスアルゴリズムは、大きな対称疎行列の固有値と固有ベクトルを計算するアルゴリズムである。

を行列で表す線形変換であるとする。 あるスカラーに対して

(1)

が存在するなら、はの固有値といい、対応する（右）固有ベクトルがあることになる。

を正方行列

(2)

固有値とすると、その固有値は、次のようになる。 とすると、対応する固有ベクトルは

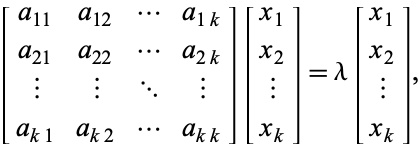(3)

となり、同次方程式

と同義となる。

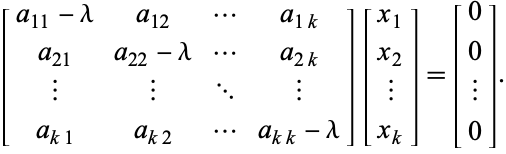(4)

式はコンパクトに

(5)

(は単位行列）と書き換えることができます。 クラマーの法則で示すように、行列式が消失する場合、連立方程式は自明でない解を持つ。 であるから、(5)式の解は

(6)

この方程式はの特性方程式として知られており、左辺は特性多項式として知られています。

例えば、行列の場合。 固有値は

(7)

で、その解として発生する。

(8)

すべての固有値が異なる場合、特性方程式が成立する。 を差し込むと、対応する各固有ベクトルの成分について独立な方程式が得られ、この系はnondegenerateと言われる。 もし固有値が倍縮退していれば、系は縮退していると言われ、固有ベクトルは線形独立でない。 このような場合、固有ベクトルが直交するという制約

(9)

（はKronecker delta）を適用すれば追加制約が得られ、固有ベクトルに対する解が得られるようになる。

固有値はWolfram LanguageでEigenvaluesを使って計算することができる。 固有ベクトルと固有値はEigensystemというコマンドで一緒に返すことができる。

(10)

の固有値が分かったとする。に恒等行列を1回加えた定数を加える。

(11)

従って新しい固有値は古い値にを加えたものと同じになります。 に定数

を掛けると

(12)

ですから、新しい固有値は以前のものに を掛け合わせたものになります

さてについて類似変換を考えてみます。 をの行列式とする。 すると

			(13)
			(14)
			(15)

だから固有値はと同様である。