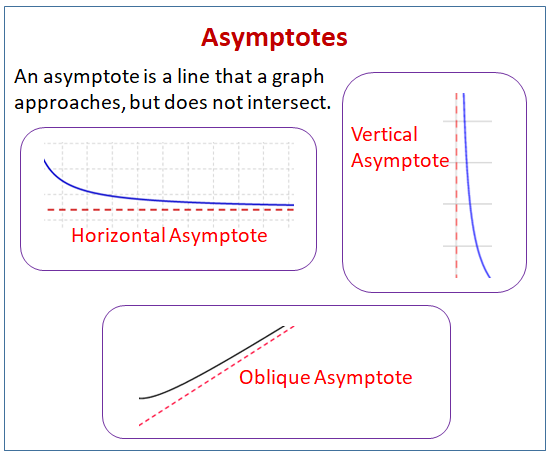
漸近線とは、グラフが近づくが、交差しない線のことです。
このレッスンでは、有理関数の垂直漸近、水平漸近、斜め漸近の求め方を学びます。
関連項目：
微積分の他のレッスン

次の図は、さまざまな種類の漸近を示しています：水平漸近、垂直漸近、斜めの漸近です。 漸近線の求め方については、ページをスクロールしてください。

垂直漸近線の求め方

方法1：垂直漸近線の定義を用いる

曲線 x = a は、以下の文の少なくとも一つが真であれば、その曲線 y = f(x) の垂直漸近線と呼ばれます。

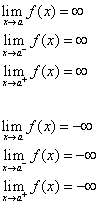方法2：

有理関数の場合、垂直漸近線は分母の0に対応する垂直線である。
有理関数f(x)が与えられたら

ステップ1：f(x)を縮小形で書く

ステップ2：x – cが分母の係数ならx = cは垂直漸近線になる

例：

の垂直漸近線を求める解決。

方法1：垂直漸近線の定義を使う

xが3に近いが3より大きい場合、分母x – 3は小さな正の数で、2xは8に近くなります。 だから、は大きな正の数である。

直感的には、

同様に、xが3に近いが3より小さい場合、x – 3は小さな負の数であり、2xは8に近くなることが分かる。 ですから、は大きな負の数です。

線分x=3は垂直漸近線です。

方法2：

ステップ1：f(x)はすでに縮小形になっています。

ステップ2：分母がx – 3なので、x = 3に垂直漸近線があります。

有理関数の垂直漸近を求める

有理関数の垂直漸近を求めるために、何を調べればよいか。

• 段階的解法を示す

有理関数の垂直漸近を求める。 Quick Way to Find Them

Example of finding vertical asymptotes of rational functions.

• Show Step-by-step Solutions

How to find vertical asymptotes for rational functions

• Show Step-by-step Solutions

How to determine the horizontal Asymptote?

方法1：水平漸近の定義を使う

曲線y＝f（x）の水平漸近は、

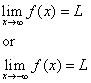
のどちらかの場合、水平漸近と呼ばれます。

有理関数f(x)について、分子のxの次数が分母のxの次数より小さければ、y = 0が水平漸近線となる。

分子のxの次数が分母のxの次数と等しければ、y=cで、cは先頭の係数を割って得られる。

の例です。

関数の水平・垂直漸近線を求めよ。

解答を示します。

方法1：

分子と分母の両方をxで割る。

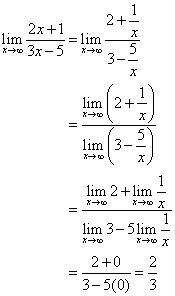
直線は水平漸近線である。

方法2：

分子のxの次数と分母のxの次数は等しい。

先頭の係数を割ると

直線は水平漸近線となる。

有理関数の水平漸近を求めるショートカット

有理関数の水平漸近を非常に簡単に求めることができるいくつかのコツ

• ステップバイステップの解法を表示

このビデオでは、水平漸近の基本概要を学びます。 与えられた有理関数に水平漸近があるかどうか、またそれが何であるかを判断します。

• Show Step-by-step Solutions

このビデオでは、水平漸近の規則についてさらに詳しく説明します。

の場合、曲線 y = f(x) と直線 y = mx + b の垂直距離は 0 に近づくので、直線 y = mx + b は斜漸近と呼ばれます。

有理関数では、分子の次数は分母の次数より 1 多いときに斜漸近が発生します。 このような場合、斜交漸近線の方程式は長割で求めることができる。

例。

関数

の漸近線を求めよ。解答。

分母のx2 + 1は決して0ではないので、垂直漸近線はありません。

分子のxの次数は分母のxの次数より大きいので、水平漸近線はありません。

分子のxの次数は分子のxの次数より1大きいので、除法を使って斜方漸近線を得ることができます。

つまり、直線y = xが斜交漸近線です。

Finding Slant Asymptotes of Rational Functions

このビデオは、有理関数が斜交漸近線を持つとき、斜交漸近線とは何か、そして2つの例について簡単に説明します。

• 段階的に解く

有理関数の漸近線を求める（垂直、水平、斜め）

このビデオでは、有理関数の垂直漸近線と斜め漸近線を求める方法について説明します。

• Show Step-by-step Solutions

Finding All Asymptotes of a Rational Function (Vertical, Horizontal, Oblique / Slant)

ここでは、関数を見て、垂直漸近線を求め、また水平漸近線はないが、斜め漸近線は存在すると結論付けます。 268>

Try the free Mathway calculator and problem solver below to practice various math topics.私たちは、この問題を解くことができるようになりました。 与えられた例を試すか、またはあなた自身の問題を入力し、ステップバイステップの説明であなたの答えをチェックしてください。