あなたの机に平らに置かれた四角い紙を想像してください。 目を閉じてください。 紙がずれる音が聞こえます。 目を開けると、紙は変わっていないように見えます。

紙を30度回転させていないことは明らかです。

しかし、紙を時計回りか反時計回りに90度の倍数で回転したり、対角線や水平・垂直線のどちらかを横切って裏返すことはできたはずです。

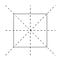
変換を視覚化するのに役立つ方法は、正方形の角に印をつけることです。

最後のオプションは、何もしないことです。 これは同一変換と呼ばれます。 これらを合わせて、正方形の対称変換と呼びます。

対称変換を組み合わせて、別の対称変換を作ることができます。 たとえば、線分 BD を横切る 2 回の反転は、90 度反時計回りの 4 回の連続回転と同様に恒等式を生成します。 垂直線に対して反転し、水平線に対して反転すると、180度の回転と同じ効果が得られます。 一般に、対称変換の組み合わせは、対称変換を生成します。 次の表は対称変換の組み合わせの規則を示している：

この表で、添え字90、180、270のRは反時計回りに90、180、270度回転することを、Hは横線を中心とした反転、Vは縦線を中心とした反転、MDは左上から右下への対角線を中心とした反転、ODはもう一方の対角線を超えた反転を意味する。 AとBの積を求めるには、Aの行からBの列へ移動します。例えば、H∘MD=R₉₀となります。

表を見て気がついたことがいくつかあります：

• 演算∘は連想的で、任意の変換A、B、Cに対してA∘(B∘C) = (A∘B)∘Cということです。
• 任意の対称変換AとBの組に対して、合成A∘Bも対称変換である
• すべてのAに対してA∘e=e∘Aとなる要素eが一つある
• すべての対称変換Aに対して。 A-¹=A-¹∘A=e

したがって、正方形の対称変換の集まりは、合成と組み合わせて、群という数学的構造を形成すると言うことができます。 この群をD₄といい、正方形の二面体群と呼びます。 これらの構造はこの記事の主題である。

群の定義

群⟨G,*⟩は、群公理を満たすGの任意の二つの要素を結合する規則*を持つ集合Gである：

抽象的には*を抑制しa*bと書いてab、*は乗法と呼ぶことがよくある。

a*b=b*aという意味で、*が可換である必要はない。 これはD₄の表を見ればわかるが、H∘MD=R₉₀がMD∘H=R₂₇₀になっている。 が可換である群をNeils Abelにちなんでabelian groupと呼ぶ。

Abelian groupは規則というより例外である。 非アベリアン・グループのもう一つの例は、立方体の対称変換である。 軸の回転だけを考えてみましょう。

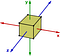
最初に Y 軸について反時計回りに 90 度回転し、次に Z 軸について反時計回りに 90 度回転すると、彼の場合は、Z 軸について 90 度回転し、次に Y 軸について 90 度回転する場合と異なる結果になります。

ある要素がそれ自身の逆であることは可能です。 0と1からなる群に2進数の足し算の演算をしたものを考える。 その表は次の通りです：

明らかに1がそれ自身の逆数であることがわかります。 これも abelian group です。 心配しないでください、ほとんどの群はこんなにつまらないものではありません。

さらに群の例をいくつか挙げましょう。

• 加算を伴う整数の集合。
• 乗算を伴う0以外の有理数の集合。
• n番目の単一根と呼ばれる多項式方程式xⁿ-1=0 の解を乗算で求めたセットです。

以下、群ではない例です。

• 自然数の足し算の集合は、負の数となる逆数が存在しないため、群ではありません。
• 乗算で0を含むすべての有理数の集合は、0/q=1となる有理数qが存在しないので、すべての要素が逆数を持つわけではないので群ではない。

群構造

群は、4公理を満たす単なる塊以上のものである。 群は内部構造を持つことができ、この構造は非常に複雑であることがあります。 抽象代数学の基本的な問題の1つは、群の内部構造がどのようなものかを決定することです。現実の世界で実際に研究されている群は、ここであげた単純な例よりもずっと大きく複雑だからです。 群Gは、HがGの部分集合であるとき、部分群Hを持ち、また

• For a,b∈H, a*b∈H and b*a∈H
• For a∈H, a-¹∈H
• the identity is an element of H

H≠G if H is a proper subgroupと言われる。 Gのうち恒等式のみからなる部分群をトリビアル部分群と呼ぶ。

非可換群は可換部分群を持つことがある。 序章で取り上げた正方二面体群について考えてみよう。 この群は abelian ではないが，回転の部分群は abelian で cyclic である：

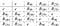
ここで群構造の例を二つ挙げることにする。

群Gがabelianでなくても、Gのすべてと通約するGの要素の集まりがある場合があります。この集まりをGの中心と呼びます。 証明：

いま、fを領域と範囲がともにGである関数とする。fの周期とは、すべてのx（G）に対してf（x）=f（ax）となる要素a（G）のことである。 証明：

有限群は有限生成である

我々は環状群が単一の要素によって生成されることを見た。 群Gのすべての要素をGの(必ずしも適切でない)部分集合Aの積として書くことができるとき、AがGを生成すると言い、これをG=⟨A⟩と書くのである。 最も「なるほど」と思わせる証明は、すべての有限群が有限の生成集合によって生成されることの証明です。 G のすべての要素は G の他の 2 つの要素の積であるから、G=⟨G⟩。 QED.

この記事の最後に、応用例を紹介します。

エラー耐性通信

デジタル情報を送信する最も簡単な方法は、固定長の2進文字列に符号化することである。 どのような通信方式も完全に干渉を受けないわけではないので、常に間違ったデータを受信してしまう可能性がある。 最尤復号法は、伝送エラーを検出し修正するための簡単で効果的なアプローチです。

長さ n の 2 進文字列、または単語の集合を 𝔹ⁿ とします。 すべての要素はそれ自身の逆数であることに注意してください。 符号 C は 𝔹ⁿ の部分集合です。 以下は𝔹⁶のコードの例です：

C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}

コードの要素をコードワードと呼びます。 コードワードだけが伝送されます。 干渉によって伝送されるワードのビットが変化すると、エラーが発生すると言われています。 2つのコードワードa、b間の距離d(a,b)は、2つのコードワードが異なる桁数です。 あるコードの最小距離は、そのコードワードのうちの任意の2つの間の最小の距離です。 9092＞＜4374＞最尤復号法では、誤りを含む可能性のある単語xを受信した場合、受信機はxをd(a,x)が最小となるようなコードワードaとして解釈すればよいことになっています。 最小距離mの符号に対して、これは常に（1）mビット以下の変化をする誤りを検出し、（2）1/2（m-1）ビット以下の変化をする誤りを訂正することができることを示そう。

この例のコードでは、m=3、コードワード011101に関する半径½（m-1）=1の球は{011101、111101、001101、011001、010101、011111、011100}となります。 9092>

さて、それはいいとして、これが群論とどんな関係があるのでしょうか。

𝔹ⁿのコードが部分群を形成することはありえます。 この場合、そのコードはグループコードであると言います。 群コードは有限群なので、有限生成です。

符号は、各コードワードの最初の数ビットを情報ビット、最後のビットをパリティビットと呼ぶように指定することができます。 例のコードCでは、最初の3ビットが情報ビットで、最後の3ビットがパリティ・ビットです。 パリティビットはパリティチェック方程式を満たしています。 コードワード A₁A₂₃A₄A₅A₆に対して、パリティ方程式は、A₄=A₁+A₂, A₅=A₂+A₃, A₆=A₁+A₃ である。 パリティ方程式は、エラーに対するもう一つの保護層を提供します。パリティ方程式のいずれかが満たされない場合、エラーが発生したことになります

ここで、私たちが行うことを説明します。 m個の情報ビットとn個のパリティビットを持つコードワードを求めるとする。 グループコードを生成するために、m行、m+n列の行列を書きます。 最初のm列で形成されるブロックに、m×mの単位行列を書きます。 m+1≦j≦m_nのj列目には、パリティビットAⱼのパリティ方程式にAₖが現れる場合は1を、それ以外は0を書きます。 例のコードでは、行列は次のようになります：

こうした行列をグループコードの生成行列と呼びます。 行がCを生成することは直接確認できます：

任意の生成行列の行はグループコードCの生成集合を形成します証明：

• 同一性と逆行列です。
• 閉包：A,B∈Cならば、AとBは生成行列の行の和なので、A+Bも生成行列の行の和である。 したがってA+B∈C.

これでコードが生成できましたが、次に有用なコードを生成する方法を示します。

重みw（x）をxの1の数と定義します。例えばw（100101）=3です。 w(x)=d(x,0)ここで0は桁がすべて0の単語であることは自明である。 符号の最小の重さWは、符号の中で最も少ないものを持つ非ゼロのコードワードの重さです。 最小距離mの符号では、d(x,0)≧mですから、w(x)≧mでW=mとなります。

ある語が符号語とみなされるには、一連のパリティ検査方程式を満たす必要があることを思い出してください。 この例のコードでは、A₄=A₁+A₂₂, A₅=A₂+A₃, A₆=A₁+A₃ がこれにあたります。 また、これらを連立一次方程式として書くこともできる：

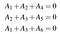
これ自体はドットプロダクトで書くことができる。

あるいはもっとコンパクトに Ha=0 として a=(A₁,A₂₃,A₄,A₅,A₆)、H はコードのパリティチェックマトリックスを示します。

もしw（a）≦2ならHa＝0にはならないことが直接計算で確認できる。 一般に、最小の重みはt+1であり、tはHのt個の列の集まりが0にならない（すなわち線形独立である）ような最小の数である。 これを証明すると、線形代数にほんの少し入りすぎてしまいます。

もしこれで怖くなったら、心配しないでください。 先ほど述べた結果は、H のすべての列が非ゼロで、2 つの列が等しくない場合、最小の重み、したがってコードの最小距離は少なくとも 3 であることを意味するという事実を利用すれば、それなしでいくつかの非常に良いコードを作成することができます。 これは非常に良いことです。もし私たちの通信システムが100ワード送信するごとに1ビットの誤りがあると予想される場合、1万ワード送信するうちの1ワードだけが修正されない誤りを持ち、100万ワード送信するうちの1ワードが検出されない誤りを持つことになります。 2つの列が同じでなく、0だけの列がないように、1と0で行列を埋めます。

例として、単純な8ワードコードが必要で、基本的な誤り検出だけで、訂正は必要ないので、最小距離は2で済むとします。 情報ビットが3つ、パリティビットが2つ必要です。 以下のパリティ検査行列を書き出します：

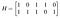
等しい列の組が2つあるので、t列の任意の集まりが線形独立である最小のtは1であり、最小重み、したがって私が持つ最小距離は2である。 行はパリティ検査式A₄=A₁+A₃、A₅=A₁+A₂+A₃を表している。 したがって私の生成行列は次のようになる：

そしてこの行列の行はコードグループを生成する。

• {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}

締めの言葉

抽象代数は広範囲な意味を持つ深い科目ですが、非常に学びやすい科目でもあります。

この記事を書くことを最初に思いついたとき、本当はルービックキューブについて話したかったのですが、最終的には群論の最も基本的な考えだけでカバーできる例を選びたかったのです。

私の大学での抽象代数の講義は、チャールズ・ピンターの「A Book of Abstract Algebra」という本に基づいて行われましたが、これはわかりやすい本です。

最後に、引用されていない画像はすべて私自身のオリジナル作品であり、帰属表示をした上で使用することができます。 いつものように、訂正や説明の要望があれば、感謝します。

。