学習目標
- 電子軌道の3D表現を理解する
軌道はボーアの軌道を量子力で改良したものです。 半径が固定された単純な循環軌道の概念とは対照的に、軌道は電子を含む確率が異なる数学的に導き出された空間の領域である
電子確率分布を表す一つの方法は、以前に水素の1s軌道で示された。 Ψ2は与えられた空間(例えば1立方ピコメートル)の中で電子を見つける確率を与えるので、核からの距離(r)に対するΨ2のプロットは確率密度のプロットとなる。 1s軌道は球対称なので、任意の地点で1s電子が見つかる確率は、原子核からの距離だけに依存する。 確率密度が最も大きくなるのは、୧⃛(๑⃙⃘◡̈๑⃙⃘) (原子核において)そして、距離が長くなるにつれて着実に減少する。
一方、半径r1, r2, r3,…, rx – 1, rxの一連の球殻上のすべての点に電子が存在する確率をtogetherhe(rx)で追加すると、半径確率(原子核から距離πで1s電子を発見する確率)を計算することができる。 つまり、原子をタマネギの層のように薄い同心円状の殻に分割し、それぞれの球殻上に電子が存在する確率を計算するのです。 電子の確率密度が最も高くなるのは”Ⓐ= 0 “であり(図Ⓐ)、ドット密度は図Ⓐの最小の球殻である”Ⓑ”で最も高くなることを思い出してください。 一方、各球殻の表面積は、 \(4πr^2) に等しく、これは \(r) が増加するにつれて非常に急激に増加する(Figure \(PageIndex{1c}) )。 球殻の表面積は、電子確率密度の減少よりもむしろ、 \(r) の増加に伴って急速に増加するため、半径方向の確率のプロットは、特定の ㎤で最大となる(Figure \(PageIndex{1d}))。 最も重要なことは、(Figure) Ⓐが非常に小さい場合、球殻の表面積が非常に小さいため、原子核の近くで電子を見つける総確率が非常に低く、原子核では電子確率は消失することです。 Most Probable Radius fo(r) the Electron in the Ground State of the Hydrogen Atom.図:水素原子の基底状態における電子の最確半径。 (a)原子の全容積をタマネギの絵のように非常に薄い同心円状の殻に分割することを想像してください。 (b) 電子確率密度Ψ2 vs ㎤のプロットでは、電子確率密度は㎤=0で最大となり、㎤の増加とともに滑らかに減少する。 したがって、ドットの密度はタマネギの最内殻で最大となる。 (c)各殻の表面積は、4πr2で表され、閾値が大きくなるにつれて急激に増加する。 (d) 各球殻にあるドットの数be(r\)を数えると、ある閾値の時に電子が見つかる確率の合計が求まる。 電子の確率密度の減少よりも、各殻の表面積の増加の方が大きいため、電子の確率と半径方向の確率である \(r) の関係をプロットすると、ピークが現れます。 このピークは電子の最確半径fo(r) 52.9pmに対応し、これはボーアの水素原子モデルで予測される半径と一致する。
水素原子では、半径確率のプロットのピークは \(r) = 0.529Å (52.9pm) で起こり、これはちょうどBohrの計算したn=1軌道の半径fo(r) のとおりである。 このように、量子力学で求めた最確半径は、古典力学で求めた半径と同じである。 しかし、Bohrのモデルでは、電子は100%の時間、この距離にいると仮定されていたのに対し、Schrödinge(rētk)のモデルでは、この距離にいるのは一部の時間だけである。 この2つのモデルの違いは、電子の波動性とハイゼンベルグの不確定性原理によるものである。 3つとも球対称であることに注意。 fo(r) the 2s and 3s orbitals, howeve(r) (and fo(r) all othe(r) s orbitals as well as), the electron probability density is not fall off smoothly with increasing \(r). 代わりに、半径方向の確率プロットで一連の極小値と極大値が観察されます(図(㊦))。 この極小は球状のノード(電子確率がゼロの領域)に対応し、球状の非ゼロ電子確率の領域と交互に現れる。 これらのノードが存在するのは、波動関数Ψの波動位相が変化した結果である。 Probability Densities fo(r) the 1s, 2s, and 3s Orbitals of the Hydrogen Atom.図は、水素原子の1s、2s、3s軌道の確率密度。 (a)原子核を含む任意の面における電子の確率密度を示している。 確率密度がゼロとなるcircula(r)領域、o(r)nodesの存在に注意。 (b)Contou(r)面は電子の確率の90%を囲んでおり、1s、2s、3s軌道の大きさが異なることがわかる。 切断面は内部の球状節理を部分的に示している。 オレンジ色のcolo(r)は波動関数の位相が正である空間の領域に対応し、青色のcolo(r)は波動関数の位相が負である空間の領域に対応する。 (c)電子の確率を核からの距離(r)の関数として全方向にプロットしたもの(半径方向の確率)では、nが大きくなると最確半径が大きくなるが、2s軌道と3s軌道は閾値が小さいときに電子の確率が大きくなる領域を持っている。
s軌道(l=0)
nが大きくなるとs軌道には3つのことが起こる(図(㊦PageIndex{2})):
- 核から遠ざかり、大きくなる
- 多くの節を含む。 This is simila(r) to a standing wave that has regions of significant amplitude separated by nodes, points with zero amplitude.
- Fo(r) a given atom, the s orbitals also become highe(r) in energy as n increases because of thei(r) increased distance from the nucleus.
³”R” or ³”r” as a registered atomic, The s orbitals is also highhe(r) in energy as n increases.
軌道は一般に電子密度の90%を囲む立体面として描かれ、図中の(b)の水素1s、2s、3s軌道がそうであったように、電子密度の90%を囲む立体面として描かれる。 このような図面では、軌道の相対的な大きさはわかるものの、2s、3s軌道の球状節点は90%面の内側にあるため、通常、球状節点が表示されない。 幸いなことに、球面結節の位置は化学結合の観点からは重要ではない。 lの値が大きくなると、ある部分殻に含まれる軌道の数が増え、軌道の形も複雑になってきます。 2p副殻はl=1であり、mlは-1、0、+1の3つであるため、2p軌道は3つ存在する。 Electron Probability Distribution fo(r) a Hydrogen 2p Orbital. 電子密度ゼロの結節面は2p軌道の2つのローブを分離している。 図中の色は、図と同様に波動関数の位相が正(オレンジ)、負(ブルー)の領域に対応している。
図中に、水素2p軌道の1つの電子確率分布fo(r)を示す。 この軌道はz軸方向に2つのローブがあり、xy平面では電子密度が0であるため(つまりxy平面が節面)、 \(2p_z) orbitalと呼ばれる。 図に示すように、2つの2p軌道は同じ形をしていますが、それぞれx軸( \(2p_x) )とy軸( \(2p_y) )に沿った形をしています。 p軌道の節面は1つだけであることに注意してください。 いずれの場合も、2p軌道の波動関数の位相は、正の軸を指すローブが正の位相、負の軸を指すローブが負の位相となります。 これらの符号は電子の運動を記述する波の位相に対応し、正のo(r)負電荷に対応するものではないことを強調しておく。
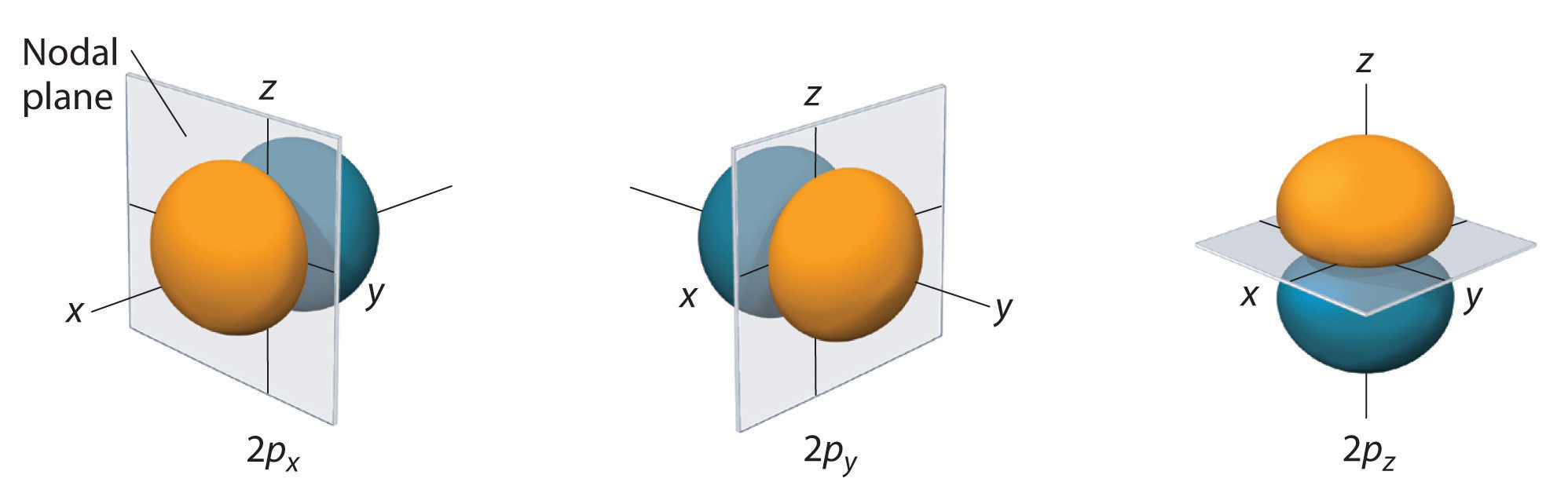
The surfaces shown into 90% of the total electron probability fo(r) (2px, 2py, 2pz orbitals). 各軌道は添え字で示された軸に沿って配向し、その軸に垂直な結節面が各2p軌道を2等分している。 波動関数の位相は、空間のx, y, o(r\) zが正の領域では正(オレンジ)、x, y, o(r\) zが負の領域では負(青)になっています。 s軌道と同様に、p軌道の大きさと複雑さは、主量子数be(r)nが大きくなるにつれ、どの原子でもfo(r)atmになる。 しかし、3p、4p、高エネルギーp軌道の90%確率曲面の形状は、基本的に図(ⅳ)と同じである。d軌道 (l=2)
l=2のサブシェルは5つのd軌道を持ち、dサブシェルを持つ最初の主殻はn=3に相当する。 5つのd軌道のml値は-2, -1, 0, +1, +2である。 水素原子の5つの等価な3d軌道。 水素の5つの電子軌道の全電子確率fo(r)の90%を囲んでいるのがこの表面である。 5つの3d軌道のfo(r)は、2つのperpendicula(r)nodal planeが交差する平面上に配置されたfou(r)lobeから構成されています。 これらのfou(r)軌道は同じ形状であるが、異なる方向性を持っている。 5番目の3d軌道である \(3d_{z^2}) は、数学的には等価であっても、形状が異なる。 異なるローブの波動関数の位相を色で示すと、オレンジ色のfo(r) positiveと青色のfo(r) negativeである。
図中の水素3d軌道は、2p軌道よりも複雑な形状である。 p軌道が1面、s軌道が0面であるのに対し、3d軌道は5面とも2面の節面を持つ。 d軌道のうち3つの軌道では、電子密度のローブがx-y面、x-z面、y-z面の間を向いており、それぞれ、 \(3d_{xy}), \(3d_{xz}), \(3d_{yz}) orbitalと呼ばれる。 第4のd軌道はx軸とy軸に沿ったローブを持つ軌道で、この軌道のことを「 \(3d_{x^2-y^2}}) orbital 」と呼びます。 5番目の3d軌道は “the \(3d_{z^2}} orbital “と呼ばれ、”the \(2p_z} orbital combined with an additional doughnut of electron probability lying in the xy plane “のようなユニークな形をしている。 このような特異な形状をしていますが、数学的にはother(r)fou(r)軌道と等価であり、エネルギーも同じであります。 p軌道とは異なり、d軌道の波動関数の位相は、対向するローブのペアが同じfo(r)である。 図に示すように、波動関数の位相が正のfo(r) は、z軸に沿った軌道の2つのローブ、負のfo(r) は、xy平面上の電子密度のドーナツである。 s軌道やp軌道と同様に、nが大きくなるとd軌道の大きさが大きくなりますが、全体の形状は図(㊦)のような形を保っています。 これらの副殻は7つのf軌道で構成される。 各f軌道は3つの節面を持つため、その形状は複雑である。 f軌道はou(r)の目的では特に重要ではないので、これ以上説明せず、lの値が大きい軌道についても全く説明しない。 そこで、電子が1個しかない原子やイオン(例えばH o(r) He+)を考えて、軌道エネルギーの議論を始める。 その結果、水素の2s軌道と2p軌道のエネルギーは同じであり、3s軌道、3p軌道、3d軌道のエネルギーも同じであることがわかる。 量子力学では、水素原子では、同じnの値を持つ軌道(例えば3つの2p軌道)はすべて縮退しており、同じエネルギーを持つことが予測される。 量子力学によって得られた水素の軌道エネルギーは、Bohの計算した許容エネルギーと全く同じであった。 しかし、ボーアのモデルでは各エネルギー準位に1つの軌道しか許されなかったのに対し、量子力学では、電子密度分布の異なる軌道がn=2主殻に4つ(2s軌道1つと2p軌道3つ)、n=3主殻に9つ、n=4主殻に16あると予想されます。主殻内の個々の軌道のlとmlの値の違いは、ほとんどの条件下での水素原子の発光・吸収スペクトルの理解には重要ではありませんが、水素原子を磁場に置いたときに観測される主線の分裂を説明することができます。 また、Figure Ⓐでは、軌道エネルギーの1/n2依存性から予想されるように、nの値が大きくなるとエネルギー準位がclose(r)とclose(r) togetherhe(r)になることが示されています。 Orbital Energy Level Diagram fo(rès) the Hydrogen Atom with a single electron. 各ボックスに1つの軌道が対応する。 軌道間のエネルギー差は、nの値が大きくなると急激に小さくなることに注意。
電子が1つしかない種の軌道のエネルギーは、ボーアの方程式のmino(r)変形で計算できる。この式は、核電荷(numbe(r) of protons in the nuclear)であるête(Zhite)を組み込むことによってother(rhite) single-electron speciesにも拡張可能である。
したがって、最も安定な軌道(エネルギーが最も低い軌道)は原子核に最も近い軌道である。 例えば、水素原子の基底状態では、1個の電子が1s軌道にあるが、第1励起状態では、原子がエネルギーを吸収して、電子がn=2軌道のいずれかに昇格した状態である。 電子が1個しかないイオンでは、軌道のエネルギーはnにのみ依存し、主殻内のすべての副殻、例えば \(p_x), \(p_y), \(p_z) orbital は縮退している。
Summary
The fou(r) chemically important types of atomic orbital corresponding to values of \(\ell = 0ờng), \(1ờng), \(2ờng), and \(3èng). 電子が原子核に存在する確率が最も高く、球面対称である。 황(n > 1) and \(ell = 0)の全ての軌道は1つ以上の節を含む。 δδδδの軌道はp軌道であり、原子核を含む節面を持つためダンベル型になります。 のある軌道はd軌道で、少なくとも2つの節面を持つより複雑な形状を持つ。 (注2)電子のエネルギーは原子核からの平均距離で決まるため、量子数の異なる原子軌道には軌道エネルギーと呼ばれる特定のエネルギーが存在する。
電子が1個しかない原子イオンでは、同じ値の軌道はすべて同じエネルギーで(縮退して)、主殻のエネルギーは(nm)の増加とともになめらかに増加する。 電子が最も低いエネルギーの軌道にある原子o(r)イオンを基底状態、1個以上の電子がより高いエネルギーの軌道を占める原子o(r)イオンを励起状態という。
Contributors and Attributions
-
Modified by Joshua Halpern (Howard University)