11月のTOTMでは、事例の圧縮機計算を紹介させていただきました。 厳密な方法の結果とショートカットの方法による値を比較しました。 厳密法はSoave-Redlich-Kwong(SRK)のような状態方程式に基づいて、必要なエンタルピーとエントロピーを計算するものであった。 このエンタルピーとエントロピーの値から、必要な電力と放電温度を決定する。 その結果、ショートカット法の精度は理想気体状態熱容量比kの値に敏感であることがわかった。
計算の観点だけでいえば、電力計算は質量流量、吸入温度と圧力、吐出温度と圧力の仕様に特に敏感である。 圧縮機は、その性能に影響を与える変数の値が変化する中で運転されることになる。 従って、圧縮機の計算で最も難しいのは、各変数の妥当な範囲の指定であり、計算そのものではない。 参考文献では、各変数の値を単一にすることは圧縮システムの正しい評価方法ではないことを強調している。
通常、熱力学計算は理想(可逆)プロセスに対して行われる。 可逆的なプロセスの結果は、その後、熱力学的効率の使用によって現実世界に適応される。 圧縮工程では、可視化できる理想的な工程が3つある。 1)等温過程(PV1=C1)、2)等エントロピック過程(PVk=C2)、3)ポリトロピック過程(PVn=C3)である。 これらのプロセスは、手計算またはコンピュータ計算のいずれによっても、必要な圧縮力を評価するための基礎として好適に使用することができる。
ドレッサーランドは、特に排気筒からのCO2圧縮のための「ほぼ一定温度」圧縮についてかなり多くの研究をしていることに注意してください。
このTOTMでは、測定された流量、組成、吸入と吐出の温度と圧力からコンプレッサーの効率を決定する方法を実演します。 状態方程式に基づく厳密な計算とショートカット法を検討し、結果を比較します。
圧縮機効率
圧縮機効率は、圧縮機の種類、サイズ、処理能力によって異なります。 これらは、コンプレッサーのテストによってのみ決定されますが、コンプレッサーメーカーは通常、良い見積もりを提供することができます。 計画目的のために、参考までに、総合的な効率について以下の値を提案します。 全体的な圧縮機の効率
|
Compressor Type |
Efficiency, η |
||
|
Centrifugal |
0.1 |
EFFECTIVITY | Efficiency, η0.170 – 0.85 |
|
高速往復動 |
0.72 – 0.85 |
||
|
低速往復動 |
0.75 – 0.85 |
1.75 – 0.75 |
|
|
Rotary Screw |
0.65 – 0.75 |
参考までにこれらの総合効率には圧縮機内のガス摩擦、機械損失(ベアリング、シール、ギアボックスなど)やギアボックス損失も含まれています。 機械的損失は、圧縮機のサイズとタイプによって異なりますが、95%は有用な計画数値です。 圧縮機ヘッドと吐出温度を計算するとき、使用される效率は等方性または多方性です(等方性效率は断熱效率と呼ばれることもあります)。 表1の総合効率に3~4%の機械損失を加えれば、一般に熱力学的効率の良い推定値が得られる。
既存の圧縮機の性能を評価するには、圧縮機効率(η)と電力要件を計算することが目的である。 標準状態でのガス体積流量(qS)またはガス質量率()
b. ガス組成(zi)
c. 吸入圧力(P1)および温度(T1)
d. 吐出圧力(P2)と温度(T2)
効率の推定-厳密な方法
市販のプロセスフローシミュレーションソフトの心臓部は状態方程式である。 その単純さと相対的な正確さから、Soave Redlich-Kwong (SRK) や Peng-Robinson などの 3 次元 EOS が使用されます。 これらの方程式は、蒸気-液体-平衡(VLE)、エンタルピー(h)、およびエントロピー(s)を計算するために使用されます。 適切な二項間相互作用係数を用いれば、これら2つの方程式のプロセスシミュレーション結果は実質的に同じになる。 したがって、この著作ではSRKのみを使用する。
等エントロピーの効率は
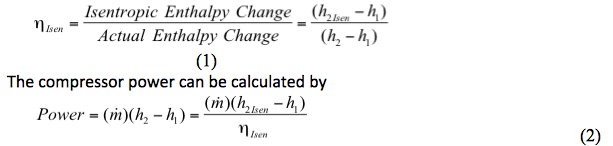
ここで、定義されます。
ηIsen = Isentropic efficiency
h1 = P1、T1、および組成(zi)
h2 = P2、T2において計算された排出エンタルピ。 と組成(zi)
h2Isen = P2(またはT2)での等エンタルピー吐出エンタルピー、S2Isen =S1、組成(zi)
![]() = マスフロー率
= マスフロー率
圧縮機効率または電力の計算には2ステップ
1.圧縮機の効率は、以下の通りである。 圧縮プロセスの理想的なまたは等エントロピーの(可逆および断熱)エンタルピー変化(h2Isen-h1)の決定。 実際のエンタルピー変化(h2-h1)の決定。
EOSに基づくステップバイステップの計算:
a. 定常状態、すなわち
bを仮定します。 供給組成が変化しないと仮定する
c. 吸引エンタルピーh1=f(P1, T1, and zi)とエントロピーs1=f(P1, T1, and zi)をEOS
d で計算する。 等エントロピー過程を仮定し、s2Isen=f(P2、T2Isen、zi)=s1=f(P1、T1、zi)
e.とする。 zi、T2(またはP2)、s2Isenが既知の場合、放電状態での理想エンタルピー(h2Isen)を計算する。 zi、T2、P2が既知で、放電状態での実際のエンタルピー(h2)を計算する。 等エントロピー効率を式1により計算する:µIsen = (h2Isen – h1)/(h2 – h1)
h. 式2により電力を計算:![]()
効率の推定 – ショートカット法
等方性経路指数(k)または理想気体熱容量比(k=CP/CV)は、2013年5月のTOTMで示された相関によって計算することができます。
![]()
ここで:
T = 温度、K(°R)
![]() = ガス相対密度;ガス分子量の空気分子量に対する比
= ガス相対密度;ガス分子量の空気分子量に対する比
A = 0.000272 (0.000151)
等方性経路に基づく実際の放電温度は、

等方性効率、
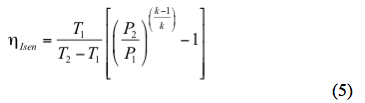
同様に解けば推定することができる。 2594>

上式を解いてポリトロピック経路係数(n)を求めれば、ポリトロピック経路による実際の吐出温度を推定することができる。

同様に、ポリトロピック経路に基づく実際の放電温度は、以下のようにして推定できる(ηPoly)。

等方性頭部は、
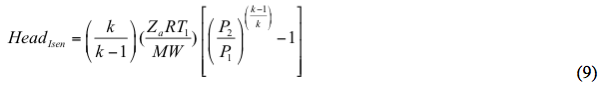
Similarly によって計算される。 ポリトロピックヘッドは
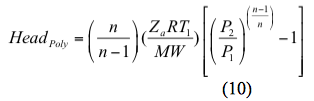
等方性(可逆・断熱)プロセスの場合、電力は
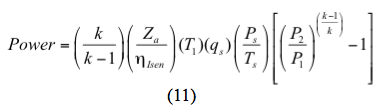
あるいはポリトロピックプロセスの場合は
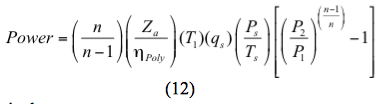
で計算されます。
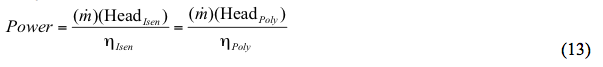
ところ。
Head = コンプレッサヘッド、m(ft)
Power = コンプレッサ電力、kW(HP)
R = 万能ガス定数、848 kg-m/(kmol-K) or (1545 ft-lbf/(lbmol-°R))
PS = 標準状態圧力、(ft/ft)
Power = 圧縮機電力、kW(ft)
Power = 圧縮機電力、kW(ft) = 圧縮機電力、kW(ft) kPa (psia)
P1 = 吸入圧力、kPa (psia)
P2 = 吐出圧力、kPa (psia)
TS = 標準状態温度、K (°R)
T1 = 吸入温度、K (°R)
T2 = 吐出温度.kPa (psia)
T1 = 吸入温度、kPa (°R)
P2 = 吐出圧力、kPa (psia)
TS = 標準状態温度、kPa (psia) K (°R)
qS = 標準状態での気体体積率, Sm3/d (scf/day)
Za = 平均ガス圧縮率 = (Z1+Z2)/2
Z1 = 吸入条件のガス圧縮率
Z2 = 吐出条件のガス圧縮率
MW = ガス分子量
電力計算は圧縮段階ごとに行い、単一の駆動機に接続したすべての段階について合計してください。
ショートカット法
a の段階的な計算。 T=(T1+3T2)/4で定義される平均温度を用いて、式3により等エントロピー指数(k)を算出する。 この平均温度の形式は、厳密な方法とショートカット法の結果の間のより良い一致を得るために定義された。 等エントロピー効率(ηIsen)を式5で計算する。 ポリトロピック係数(n)を式7.
dで計算する。 8.
e式によりポリトロピック効率(ηPoly)を計算する。 等エントロピーヘッドとポリトロピックヘッドをそれぞれ式9と式10で計算する。
f. 式11または12により、1段あたりの必要動力を計算する。
ケーススタディ
天然ガス混合物を3段の遠心圧縮機で圧縮する。 そのプロセスフロー図を図1に示す。 各段の圧力、温度の測定値を表1に示す。 また、測定されたフィード組成、流量、および計算された分子量と相対密度を表2に示します。
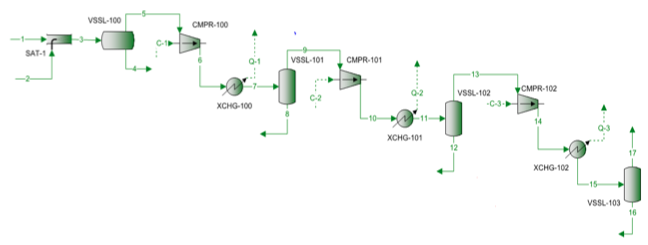
Figure 1. 3 段階圧縮のプロセスフロー図
Table 1. 3段圧縮の測定温度と圧力
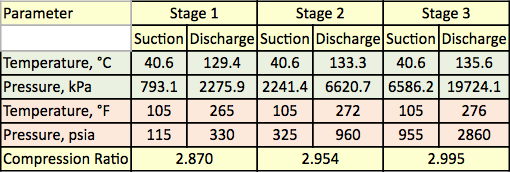
表2. 圧縮3段のガス分析値と流量
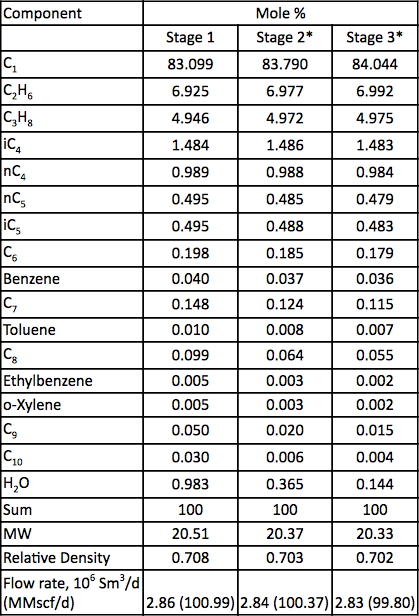
* 計算値
結果と考察
図1に示したプロセスフロー図は、SRK EOSを使って厳格な計算を実行するためにProMaxソフトウェアでシミュレーションしたものです。 このプログラムは、ポリトロピック効率、等エントロピック効率、ヘッド、および圧縮力を計算した。 また、等エントロピー経路指数(k)、ポリトロピック経路指数(n)も計算された。 これらの計算結果は、SRKヘディングの3つのステージすべてについて、表2に示されている。 ProMaxで行った計算は、厳密なセクションで説明したaからhまでのステップバイステップと非常によく似ています。 また、表2には、ショートカットの見出しの下で対応する値に対するショートカットの計算結果も示されている。 ショートカットの計算は、ショートカット法の項で説明したaからfまでのステップバイステップに基づいている。 各段階における厳密法とショートカット法との誤差率も表2に示した。 表2より、ステージ1、2では、優れた一致が得られていることがわかる。 しかし、第3ステージの等方性指数と多方性指数については、高圧運転により理想ガス状態から大きく外れているため、より大きな偏差が見られる。 厳密な計算結果とショートカット計算結果のまとめ
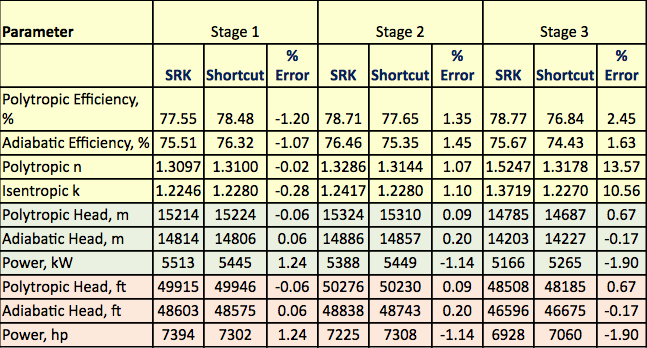
結論
表2より、ショートカットと厳密な結果がよく一致していることがわかる。 設備計算や計画立案において、厳密法とショートカット法の結果の差は無視できる程度である。 ステージ3では、高圧運転で理想ガス状態の条件から大きく外れるため、等エントロピー指数(k)に大きな誤差が見られます。
ProMaxで計算した等エントロピー指数(k)は、理想ガス状態の熱容量(CP/CV)比ではありません。 入口から出口までの等エントロピーの経路を得るために必要な等エントロピー指数の値です。 その値は、その経路の積分として計算される。 したがって、真の等エントロピーの経路を表す「平均値」のようなものである。
この「k」の誤差は、性能試験を発注する際に、どの相関を使用するかを指定することの重要性を示しています(つまり、追加の詳細については ASME PTC-10 を参照してください)。 詳細については、2010年8月と9月のTOTMを参照してください。
また、機械の状態を評価するために「n」とポリトロピック効率を傾向付ける場合、測定機器/装置(温度および圧力変換器)の相対的な精度と、圧縮機性能を元の性能曲線(実際のガス量流量対速度)にマッピングすると、毎日の評価に多くの誤りの可能性をもたらすことに注目すべきかもしれません。
ショートカット法の精度は、kとnの値に依存することに注意してください。 厳密な方法で計算された等エントロピー経路指数(k)とのより良い一致を得るために、ショートカット法における平均温度の定義を調整した。
同様のケースや運用上の問題を最小限に抑える方法について詳しく知りたい方は、G4(ガス調整と処理)、PF4(石油生産と処理設備)、ME46(コンプレッサーシステム-機械設計と仕様)、ME44(ポンプとコンプレッサーシステムの基礎)のコースに参加することをお勧めします。
ペトロスキルはこのテーマをはじめ、多くの専門コンサルティングを提供します。 これらのサービスについての詳細は、当社のウェブサイトhttp://petroskills.com/consultingをご覧になるか、[email protected] までメールでお問い合わせください。
Dr. Mahmood Moshfeghian
参考文献:
3. Soave, G., Chem. Eng. Sci., Vol.27, pp.1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B.、Ind.S.A., Vol.27, pp.1197-1203, 1972.
5. Eng. Chem. Fundam., Vol.15, p.59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, “Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J……………………
7. 「遠心圧縮機試験の重要な側面-その1」、今月のヒント、2010年8月
8. Honeywell, J. 「遠心圧縮機試験の重要な側面-その2」、今月のヒント、2010年9月
8.Honeywell, J.