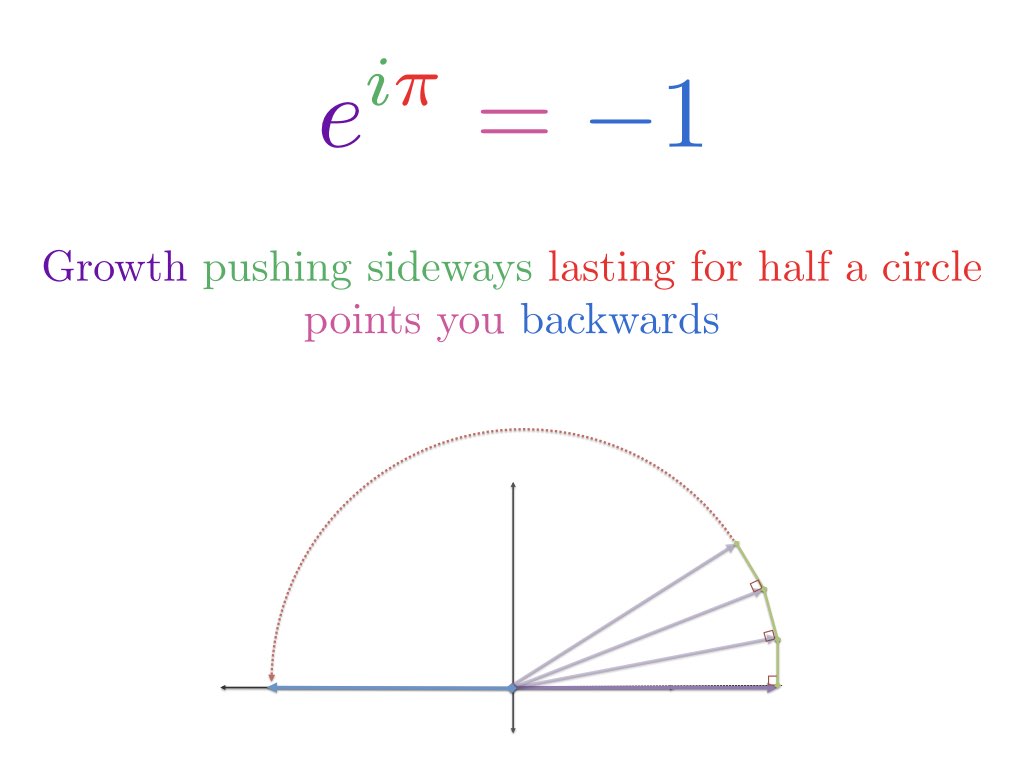Euler’s identity は不可解です:
![]()
It emerges from a more general formula:
![]()
Yowza — I am related imaginary exponent to sine and cosine ! そして、どういうわけか、π を差し込むと -1 になるのですか?
1800年代の数学者 Benjamin Peirce によれば、そうではありません。
それは絶対に逆説的で、理解できないし、それが何を意味するかもわかりませんが、それを証明したので、それが真実に違いないとわかっています。 数式は暗記するための魔法の呪文ではありません:私たちは、洞察力を見つけなければなりません。 私の場合はこうです:
Euler の公式は、円の中を移動する 2 つの等価な方法を記述している
それだけですか? この見事な方程式は、回転することについてのものですか?
- 1 という数字から始めて、掛け算を数字を変える変換と見なします。 1 \cdot e^{i \pi}$1320>
- Regular exponential growth は、ある期間、ある割合で 1 を継続的に増加させます。 虚指数関数的な成長は、ある期間1を回転させ続ける
- 「π」単位の時間で成長するということは、円をπラジアン周回すること
- したがって、$e^{i }$とは1からスタートしてπ(円の半周)回転して-1
これが大局的な見方です、詳細に見てゆきましょう。 ちなみに、$e^{i \pi} = -1$と印象づけようとする人がいたら、iのi乗について聞いてみてください。
Update: 執筆中、動画がより明確にアイデアを説明するのに役立つと思いました:
Understanding cos(x) + i * sin(x)
等号はオーバーロードされています。 あるものを別のものにする」(x = 3のように)という意味もあれば、「これら2つのものは同じ概念を表す」($sqrt{-1} = i$のように)という意味もあります。
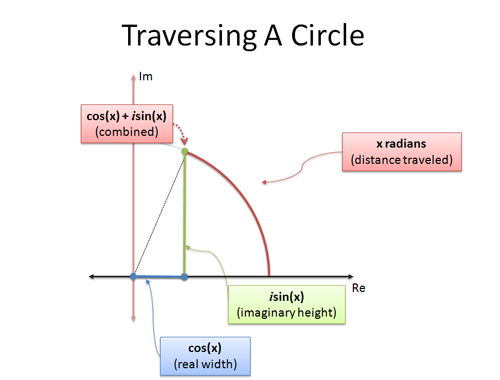
Euler の公式は後者で、円の中を移動する方法を説明する2つの公式を与えています。 円運動を三角法で調べ、xラジアン移動する場合:
- cos(x) はx座標(水平距離)
- sin(x) はy座標(垂直距離)
この記述
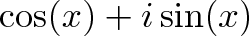
はx、y座標を単一の数値に押し込める賢い方法である。 複素数は2次元である」というアナロジーは、1つの複素数を円上の位置として解釈するのに役立ちます。
When we set x to $pi$, we’re traveling $pi$ units along the outside of the unit circle. 全周が$2}pi$なので、$2}pi$は半周になり、-1になります。
ニート:オイラーの式の右辺($cos(x) + i \sin(x)$ )は、虚数での円運動を表しています。
虚数成長とは
xとyの座標を組み合わせて複素数を作るのは難しいですが、何とかなります。 しかし、虚数指数とは何を意味するのでしょうか。
少しさかのぼって考えてみましょう。 3^4$ を見たとき、私は次のように考えます:
- 3 は ln(3) の割合で瞬時に(e を使って)成長した最終結果である。 つまり、$3 = e^{ln(3)}$
- $3^4$ は、3まで成長した後、4倍の長さで成長するのと同じです。 つまり、$3^4 = e^{ln(3) \cdot 4} = 81$
数字を単体で見るのではなく、eが「成長しなければならなかったもの」として考えることができるのですね。 3 のような実数は ln(3) = 1.1 の金利を与え、それが e の「収集」するもので、継続的に成長します。
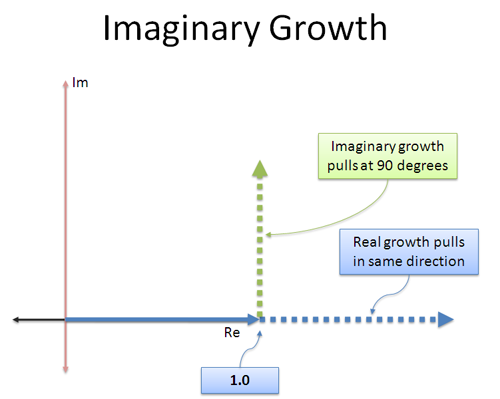
規則的成長は単純です。 3×3は元の方向に押し出され、3倍(9)になる。
想像上の成長は違う。 それは、横向きに取り付けられたジェットエンジンのようなもので、前進する代わりに、90 度で押し始めます。
一定の直交(垂直)方向の押しについての巧妙な点は、速度を上げたり下げたりせず、あなたを回転させるということです! 任意の数を取って i をかけても、その大きさは変わらず、それが指す方向だけが変わります。
直感的に、連続した虚数成長率をどう見るかは、次のとおりです。 「私が成長するとき、すでに進んでいる方向に私を押し出したり戻したりしないでください。
But We Should’t Spin Faster and Faster?
私も不思議に思っていました。 規則正しい成長は、元の方向に化合するので、1、2、4、8、16 と進み、そのたびに 2 倍して、実数の中にとどまるのです。 これは $e^{ln(2)x}$ と考えることができ、ln(2) の速度で「x」秒間瞬時に成長することを意味します。
そして、もし成長速度が 2ln(2) と ln(2) で2倍の速度だった場合、2x と x で同じ時間成長したと見えます。 ln(2) で 2 秒は 2ln(2) で 1 秒と同じ成長です。
さて、i、または 90 度上に到達するまで回転する、純粋に想像上の成長率 (Ri) があると想像してみましょう。 その速度を 2 倍の 2Ri にするとどうなるか、私たちは円からスピンするでしょうか。 2Riの速度を持つことは、単に2倍の速度で回転すること、あるいは代わりに、Rの速度で2倍の時間回転することを意味しますが、私たちは円上に留まっているのです。 2 倍の長さで回転するということは、私たちは今 180 度向いているということです。
ある指数関数的成長率が 1 から i まで私たちを連れて行けることがわかったら、その率を上げると、さらに回転することになるだけです。
しかし、成長率が複雑な場合 (a+bi vs Ri)、実部 (a) は通常のように成長し、虚部 (bi) は回転させることができます。 しかし、奇をてらうのはやめよう。 オイラーの公式、$e^{ix}$ は、私たちを円上に維持する純粋に虚数の成長についてです (詳細は後述)。
A Quick Sanity Check
執筆中に、私は自分自身のいくつかの質問を明確にする必要がありました。
e は 1 から始まり、1 単位の時間、100% の利息で継続的に成長するプロセスを表します。
e と書くとき、そのプロセス全体を 1 つの数字で捉えています。 つまり、$e^x$は「1から始めて、x秒間100%で成長し続ける」と言っているのであり、我々が望むように1から始めます。
しかし、指数としてのiは何をするのでしょうか。
$3^4$などの通常の指数に対して、次のように尋ねます:
- 暗黙の成長率は何でしょうか。 1から3(指数の底)へ成長しています。
- その成長率をどのように変更しますか? 私たちは成長を「e」形式に変換できます。私たちの瞬間的な成長率は ln(3) で、それを ln(3) * 4 に増やします。ここでも、指数の累乗 (4) はちょうど成長率をスケールします。
上の指数が i ($3^i$ のように) のとき、私たちの潜在成長率に i を掛ければいいんです。 つまり、古い ln(3) ではなく、ln(3) * i で成長します。
指数の上の部分は、下の部分の陰の成長率を変更します。
細かい詳細
詳しく見ていきましょう。 このeの定義を思い出してください。
この$thet $frac{100%}{n}$は各微視的期間に得た部分の利子を表します。
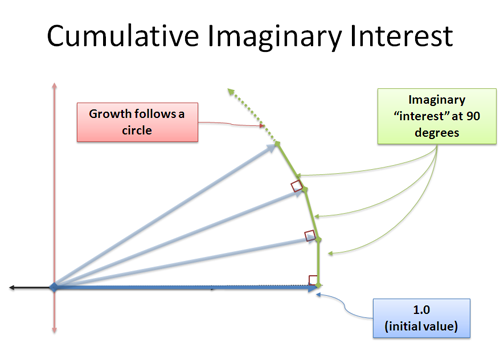
ここで、新しくできた利息は、90度の方向で私たちに加算されます。 意外なことに、これは長さを変えません。これは厄介な概念で、斜辺がより大きくなければならない三角形を作るように見えるからです。 これは、三角形の斜辺を大きくしなければならないように見えるからです。私たちが扱っているのは限界であり、余分な距離は私たちが指定した誤差の範囲内です。 これは別の日に取り組みたいことですが、私の言葉を借りれば、連続的な垂直方向の成長はあなたを回転させるでしょう。
私たちは i 単位の成長を無限に小さな増分で適用し、それぞれが 90 度の角度で私たちを押し出します。 その代わり、周囲を |i| = 1 (i の大きさ) だけ這うことになります。
そして、円を這う距離はラジアン単位の角度なのです! 円運動を表現する別の方法を見つけました!
円運動を得るには。
つまり、オイラーの公式は「指数関数的な虚数成長が円をなぞる」と言っているわけです。 そしてこの道筋は、虚数平面上でサインとコサインを使って円を移動するのと同じです。
この場合、一定の速度で円を移動するので、「指数的」という言葉が紛らわしいのです。 ほとんどの議論では、指数関数的な成長は累積的な複合効果を持つと仮定されています。
いくつかの例
あなたは本当に私を信じていないのでしょうか?
例: $e^i$
xはどこでしょうか。 直感的に、電卓を使わなくても、「単位円に沿って1ラジアン進む」という意味であることが分かります。 頭の中では、「e」が100%で1ずつ同じ方向に伸びようとしていますが、「i」はボールを動かし続けるので、「1」は円の縁に沿って伸びることになります:
あまりきれいな数字ではないですが、これでOKです。
例: $3^i$
これはトリッキーです — 私たちの標準的な形式ではありません。 しかし、
私たちは、期間終了時に 3 倍の初期成長、つまり ln(3) の瞬間的な速度が欲しいことを覚えておいてください。 しかし、i がやってきて、その ln(3) の速度を “i * ln(3)” に変えてしまいます:
私たちは、e が約 2.718 なので 100% の連続成長より少し速い ln(3) の正規の速度で変換すると思っていたのです。 しかし、いや、私は私たちを回転させました。 もしiが4のような普通の数だったら、4倍の速さで成長していたことでしょう。
私たちは、単位円周上の複素数を期待すべきです – 成長率には、私たちのサイズを大きくするものは何もありません。 方程式を解く:
つまり、($e^i$ のように) 円の周りを “1” 単位で終わるのではなく、ln(3) 単位で終わります。
例: $i^i$
数ヶ月前、私はこのことで泣いていたかもしれないです。 今日は違います! 変形を分解してみましょう。
1 から始めて、それを変えたいと思います。 3^i$ を解くように、i を基点として表される瞬間的な成長率はどのくらいか
フム。 普通はln(x)をして、1単位時間の終わりにxに到達するのに必要な成長率を求めますね。 しかし、虚数率では?
1から始めてiまで成長するためには、最初から回転を開始する必要があります。 どのくらいの速度で? そうですね、1単位時間に90度(π/2ラジアン)を得る必要があります。 ということは、回転速度は $i \frac{\pi}{ 2}$ となります。 回転しているのだから、速度は虚数でなければならないことを忘れないように!成長ではない。
このことから、1単位終了時に1.0をiにするためには、その時間で$iを90度回転させればよいことがわかりますね。 つまり、「i」を求めるには、 $e^{i \frac{pi}{2}}$ を使えばいいのです。
ふむふむ。 これでiを底とすることが記述できました。 指数はどうでしょうか。
さて、もう1つのiは速度を変えるように言っています。 つまり、i の底が意味する $i \frac{pi}{2}$ の速度で回転するのではなく、次のように速度を変換します:
i がキャンセルされて成長速度が再び実数になります!
i がキャンセルされて、成長速度が実数になりました!
i がキャンセルされて、成長速度が実数になりました。 率を回転させ、負の数に追い込んだのです。 そして、負の成長率は、私たちが縮小していることを意味します — 私たちは、$i^i$ が物事を小さくすると期待すべきです。 そして、それは実行されます:
Tada! (Google で “i^i” を検索すると、その計算機が使えます)
一息ついてください。 虚数塩基と虚数指数がどのように振る舞うべきか、直感的に理解することができます。 おっと、ボーナスとして、ln(i) がわかりましたね。$e^x$ を i にするには、e を $frac{pi}{2}$ ラジアン回転させましょう。 (i^i)^i
二重虚数指数? どうしてもというなら まず、括弧の中で成長率がどうなるかがわかります:
負の(縮む)成長率-pi/2が得られます。 そして今度はその速度をiで再び修正する:
そして今度は負の回転がある! 単位時間あたり$-Θfrac{Θpi}{2}$の速度で円の周りを回っています。 どのくらい進むのでしょうか? この指数列の一番上には暗黙のうちに「1」という時間単位があります。暗黙のデフォルトは1時間単位です($e = e^1$と同じです)。 1時間単位は$-frac{}{pi}{2}$ラジアン(-90度)または-iの回転を与えます!
そして、ちょうど、そのおかしな結果を二乗すると、
それは「ちょうど」2倍の回転です:2は正規数なので単位時間で-180度に回転率が2倍になるのです。 あるいは、-90 度の回転を 2 回続けて適用していると見ることもできます。
一見したところ、これらは本当に奇妙な指数です。 しかし、我々のアナロジーを使えば、すぐに理解できる。
Complex Growth
実数と虚数の成長を同時に行うことができる:実数の部分は我々を拡大し、虚数の部分は我々を回転させる。 実部aは「100%でa秒間成長する」、虚部bは「b秒間回転する」という意味です。 回転は、異なる方向に「押し続ける」ので、複利の利益を得られないことを覚えておいてください。 半径は $e^a$ で、角度は $e^{bi}$ で決まります。 数字をエキスパンドオトロンの中に入れて、1回でちょうどいい大きさになり(a秒)、もう1回でちょうどいい角度に回転させる(b秒)、というサイクルを2回繰り返すようなものです。 あるいは、先に回転させてから成長させることもできます!
例えば、6+8iになるための成長量を知りたいとしましょう。 これはまさに虚数の自然対数を求めているわけで、eをどのように成長させれば(6+8i)になるのか、
- 半径。 どの程度の大きさの円が必要なのでしょうか。 まあ、大きさは$¥sqrt{6^2 + 8^2} = \sqrt{100} = 10$ですね。 つまり、その量に達するには ln(10) = 2.3 秒間成長する必要があります。
- 回転する量。 その点の角度は? atan(8/6) = 53度 = .93ラジアン
- 結果を組み合わせる: ln(6+8i) = 2.3 + .93i
つまり、$e^{2.を使えばランダム点(6 + 8i)に到達できるのである。3 + .93i}$ となります。
なぜこれが役に立つのか
オイラーの公式は、円の中の運動を記述する別の方法を与えてくれているのです。 しかし、これはサインとコサインですでにできることです。
Euler の公式は極座標を使っています — 角度と距離はどうなっていますか。 繰り返しになりますが、運動を記述する2つの方法です:
- Grid system: 東に3単位、北に4単位進みます
- 極座標。 53.13度の角度で5単位進む
問題によって、極座標と直交座標のどちらが有用かは変わる。 オイラーの公式を使えば、この2つを変換して、最適な道具を使うことができます。 また、$e^{ix}$はサインとコサインに変換できるので、三角関数の公式をeの変形として書き直すことができ、非常に便利です(sin(a+b)を覚える必要はなく、導出できます — 詳しくは別の日に)。 そして、実数でも複素数でも、すべての数が e の変形であることは美しいことです。
しかし、実用性、シュミッター:最も重要な成果は、不可解な方程式も正しい類推によって直感的に理解できるようになることを実感できたことです。 オイラーの公式のような美しい方程式を魔法の呪文のままにしないでください–方程式の内側にある洞察を見るために、あなたが知っている類推を構築してください。
Appendix
The screencast was fun, and feedback is definitely welcome.スクリーンキャストは楽しかったです。
- Brian Slesinsky がオイラーの公式についてきちんとしたプレゼンテーションをしています
- Visual Complex Analysis にオイラーの公式についての素晴らしい議論があります — Google Book Preview の 10 ページを見てください
- Math and Analogies でオイラの恒等式をもっと視覚的に説明する講演をしました。
Other Posts In This Series
- A Visual, Intuitive Guide to Imaginary Numbers
- Intuitive Arithmetic With Complex Numbers
- Unstanding why complex multiplication works
- Intuitive Guide to Angles.Odyssey Intuative Guides to the Angles.Odyssey Unknown Mapper’s Angels.Dies. Intuative Guides to the Angels.Odyssey Intuive Guides.Dies, Degrees and Radians
- Intuitive Understanding Of Euler’s Formula
- An Interactive Guide to The Fourier Transform
- Intuitive Guide to Convolution直感的にわかるサイン波
- 直感的にわかる線形代数
- プログラマーの直感でわかる行列の掛け算
- 虚数乗算 vs. 実数乗算
- プログラマーの直感でわかる行列の掛け算
- プログラマーの直感でわかる行列の掛け算1320 虚数指数