Leerdoelen
- De 3D-weergave van elektronische banen begrijpen
Een orbitaal is de kwantummechanische verfijning van de baan van Bohr. In tegenstelling tot zijn concept van een eenvoudige cirkelbaan met een vaste straal, zijn orbitalen wiskundig afgeleide gebieden van de ruimte met verschillende waarschijnlijkheid van het bevatten van een elektron.
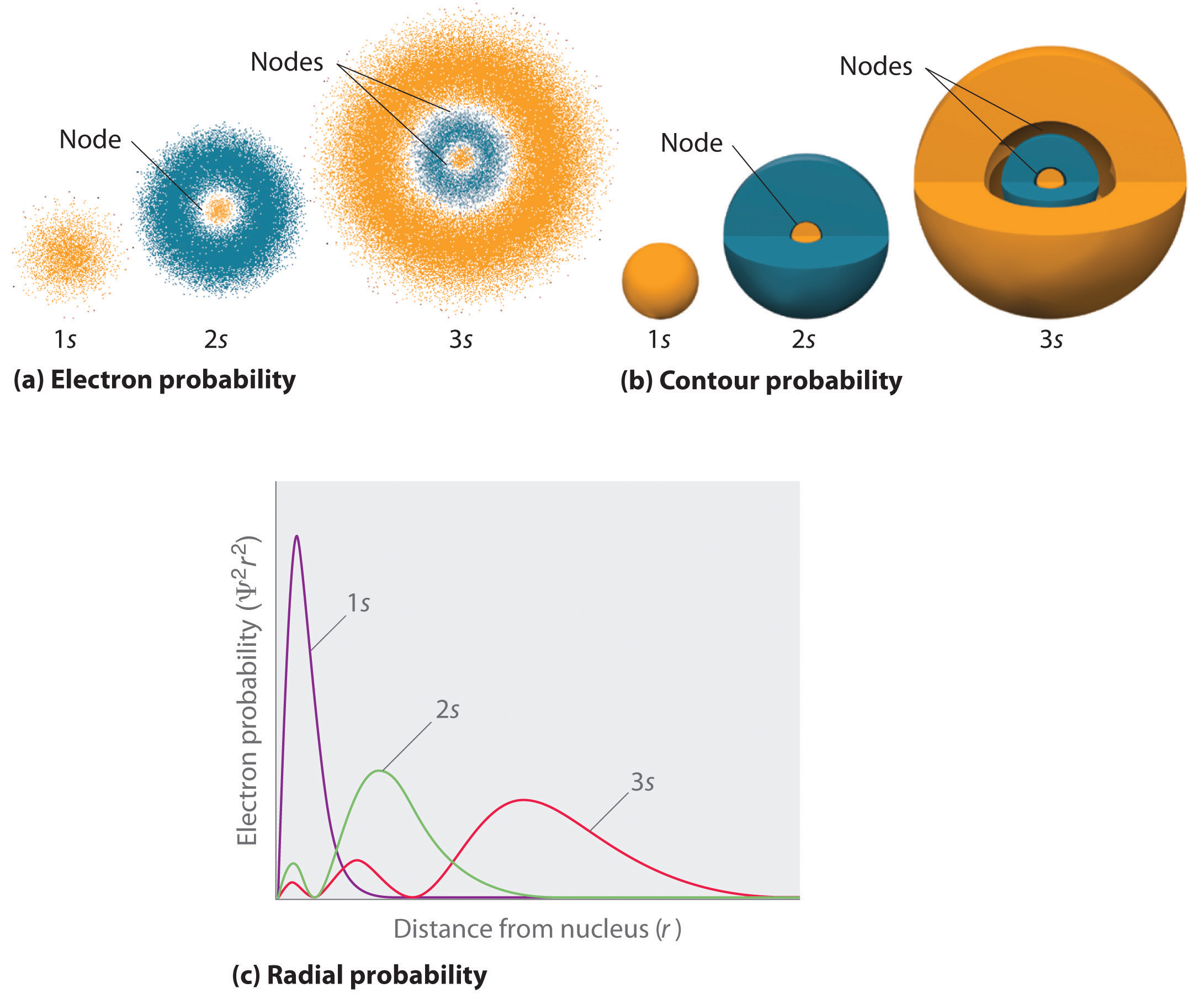
Een manier om elektron waarschijnlijkheidsverdelingen weer te geven werd eerder geïllustreerd voor de 1s orbitaal van waterstof. Omdat Ψ2 de kans geeft om een elektron in een gegeven volume ruimte (zoals een kubieke picometer) te vinden, is een grafiek van Ψ2 versus de afstand tot de kern (r) een grafiek van de kansdichtheid. De 1s-baan is bolvormig symmetrisch, dus de kans om op een bepaald punt een 1s elektron te vinden hangt alleen af van de afstand tot de kern. De kansdichtheid is het grootst bij (bij de kern) en neemt gestaag af met toenemende afstand. Bij zeer grote waarden van r is de elektronenkansdichtheid zeer klein, maar niet nul.
De radiale kans (de kans om een 1s elektron te vinden op een afstand \(r\) van de kern) kunnen we daarentegen berekenen door de kansen van een elektron op alle punten van een reeks van x bolvormige schillen met straal r1, r2, r3,…, rx – 1, rx bij elkaar op te tellen. In feite verdelen we het atoom in zeer dunne concentrische schillen, zoals de lagen van een ui (figuur), en berekenen we de kans dat zich in elke bolvormige schil een elektron bevindt. Bedenk dat de elektronendichtheid het grootst is bij r = 0 (figuur), zodat de puntdichtheid het grootst is voor de kleinste bolschilden in deel (a) van figuur. Daarentegen is de oppervlakte van elke bolvormige schil gelijk aan ƒ(4πr^2), die zeer snel toeneemt met toenemende ƒ(r) (figuur ƒ(1c)). Omdat de oppervlakte van de sferische schillen sneller toeneemt met toenemende \(r) dan de elektron waarschijnlijkheidsdichtheid afneemt, heeft de plot van radiale waarschijnlijkheid een maximum op een bepaalde afstand (figuur \(r)\)). Het belangrijkste is dat bij een zeer kleine afstand de oppervlakte van een bolvormige schil zo klein is dat de totale kans om een elektron dicht bij de kern te vinden zeer klein is; bij de kern verdwijnt de elektronenkans (figuur \(\PageIndex{1d}\)).

Voor het waterstofatoom komt de piek in de radiale waarschijnlijkheidsplot voor bij 0,529 Å (52,9 pm), hetgeen precies de straal is die door Boh is berekend voor de n = 1 baan. De meest waarschijnlijke straal verkregen uit de kwantummechanica is dus identiek aan de straal berekend uit de klassieke mechanica. In het model van Bohr werd echter aangenomen dat het elektron 100% van de tijd op deze afstand is, terwijl het in het model van Schrödinge(r) slechts een deel van de tijd op deze afstand is. Het verschil tussen de twee modellen is toe te schrijven aan het golfachtige gedrag van het elektron en het Heisenberg onzekerheidsprincipe.
Figuur vergelijkt de elektron waarschijnlijkheidsdichtheden voor de waterstof 1s, 2s, en 3s banen. Merk op dat ze alle drie sferisch symmetrisch zijn. Voor de 2s en 3s banen (en ook voor alle andere s-banen) neemt de elektronendichtheid echter niet gelijkmatig af met toenemende \(r). In plaats daarvan wordt in de radiale waarschijnlijkheidsgrafieken een reeks minima en maxima waargenomen (figuur \PageIndex{2c}}). De minima komen overeen met sferische knooppunten (gebieden van nul elektron waarschijnlijkheid), die worden afgewisseld met sferische gebieden van niet-nul elektron waarschijnlijkheid. Het bestaan van deze knooppunten is een gevolg van veranderingen van de golffase in de golffunctie Ψ.
s Banen (l=0)
Er gebeuren drie dingen met s Banen als n toeneemt (figuur (\PageIndex{2}})):
- Ze worden groter en strekken zich verder van de kern uit.
- Ze bevatten meer knooppunten. Dit is te vergelijken met een staande golf die gebieden heeft met een aanzienlijke amplitude, gescheiden door knopen, punten met nul amplitude.
- Voor een gegeven atoom worden de s-banen ook hoger in energie als n groter wordt vanwege de grotere afstand tot de kern.
Orbitalen worden meestal getekend als driedimensionale oppervlakken die 90% van de elektronendichtheid omsluiten, zoals te zien is bij de waterstof 1s, 2s en 3s orbitalen in deel (b) in figuur. Hoewel dergelijke tekeningen de relatieve grootte van de banen laten zien, laten ze normaal gesproken niet de bolknopen in de 2s en 3s banen zien, omdat de bolknopen binnen het 90% oppervlak liggen. Gelukkig zijn de posities van de sferische knopen niet belangrijk voor de chemische binding.
p Orbitalen (l=1)
Alleen s-orbitalen zijn sferisch symmetrisch. Naarmate de waarde van l toeneemt, neemt het aantal banen in een bepaalde subschil toe, en worden de banen complexer van vorm. Omdat de 2p-subschil l = 1 heeft, met drie waarden van ml (-1, 0 en +1), zijn er drie 2p-banen.
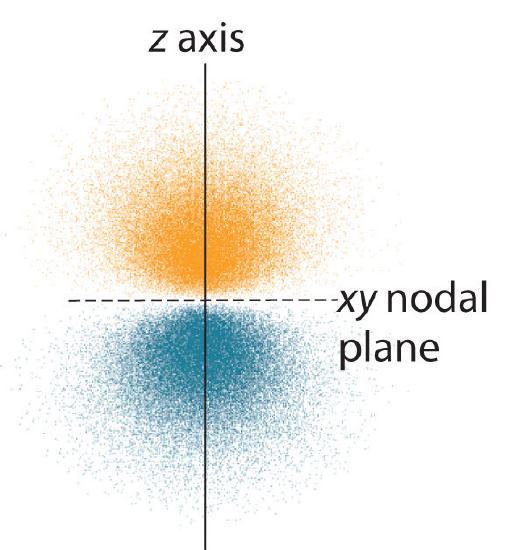
De elektronenkansverdeling voor(r) een van de 2p-banen van waterstof is weergegeven in figuur(r). Omdat deze baan twee lobben van elektronendichtheid langs de z-as heeft, met een elektronendichtheid van nul in het xy-vlak (d.w.z. het xy-vlak is een knooppuntvlak), is het een 2p-z-baan. Zoals te zien is in figuur, hebben de andere twee 2p-banen dezelfde vorm, maar ze liggen respectievelijk langs de x-as (2p_x) en de y-as (2p_y). Merk op dat elke p-baan slechts één knooppuntvlak heeft. In elk geval is de fase van de golffunctie voor elk van de 2p orbitalen positief voor de lob die langs de positieve as wijst en negatief voor de lob die langs de negatieve as wijst. Het is belangrijk te benadrukken dat deze tekens overeenkomen met de fase van de golf die de elektronenbeweging beschrijft, niet met positieve of negatieve ladingen.
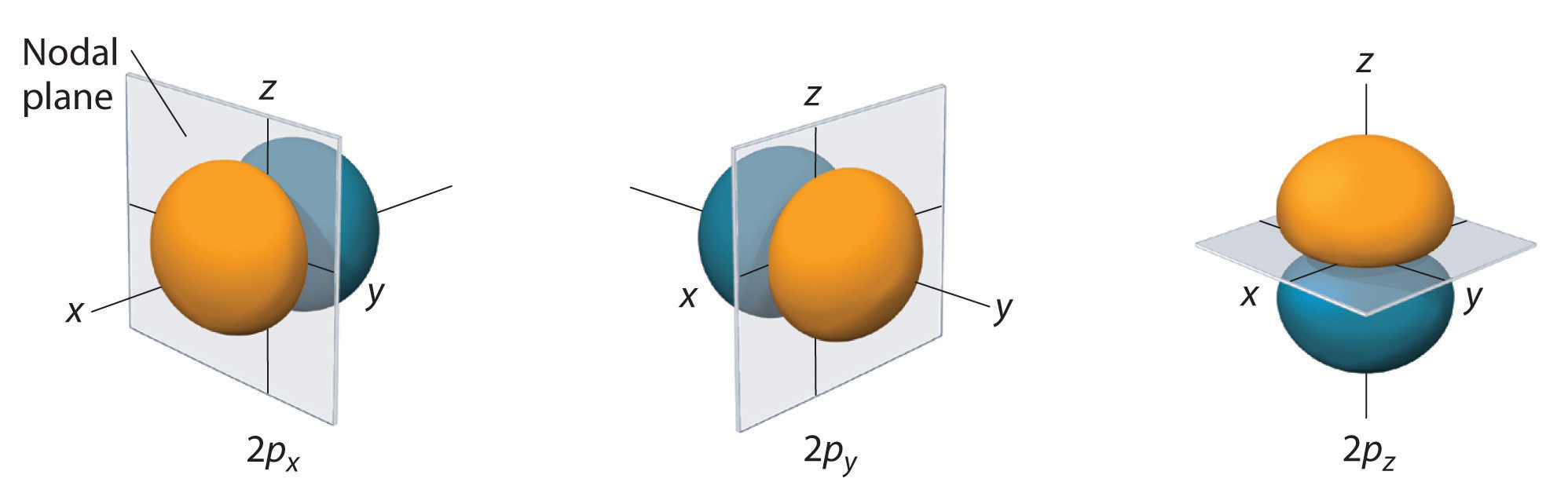
De afgebeelde oppervlakken omsluiten 90% van de totale elektronwaarschijnlijkheid fo(r) de 2px-, 2py- en 2pz-banen. Elke orbitaal is georiënteerd langs de as aangegeven door het subscript en een knooppuntvlak dat loodrecht staat op die as doorsnijdt elke 2p orbitaal. De fase van de golffunctie is positief (oranje) in het gebied van de ruimte waar x, y, o(r)z positief is en negatief (blauw) waar x, y, o(r)z negatief is. Net als bij de s-banen neemt de grootte en complexiteit van de p-banen voor elk atoom toe naarmate het hoofdkwantumgetal n toeneemt. De vormen van de 90% waarschijnlijkheidsoppervlakken van de 3p, 4p, en hoger-energetische p-banen zijn echter in essentie gelijk aan die in figuur
d-banen (l=2)
Subschillen met l = 2 hebben vijf d-banen; de eerste hoofdschil met een d-subschil komt overeen met n = 3. De vijf d-banen hebben ml-waarden van -2, -1, 0, +1, en +2.
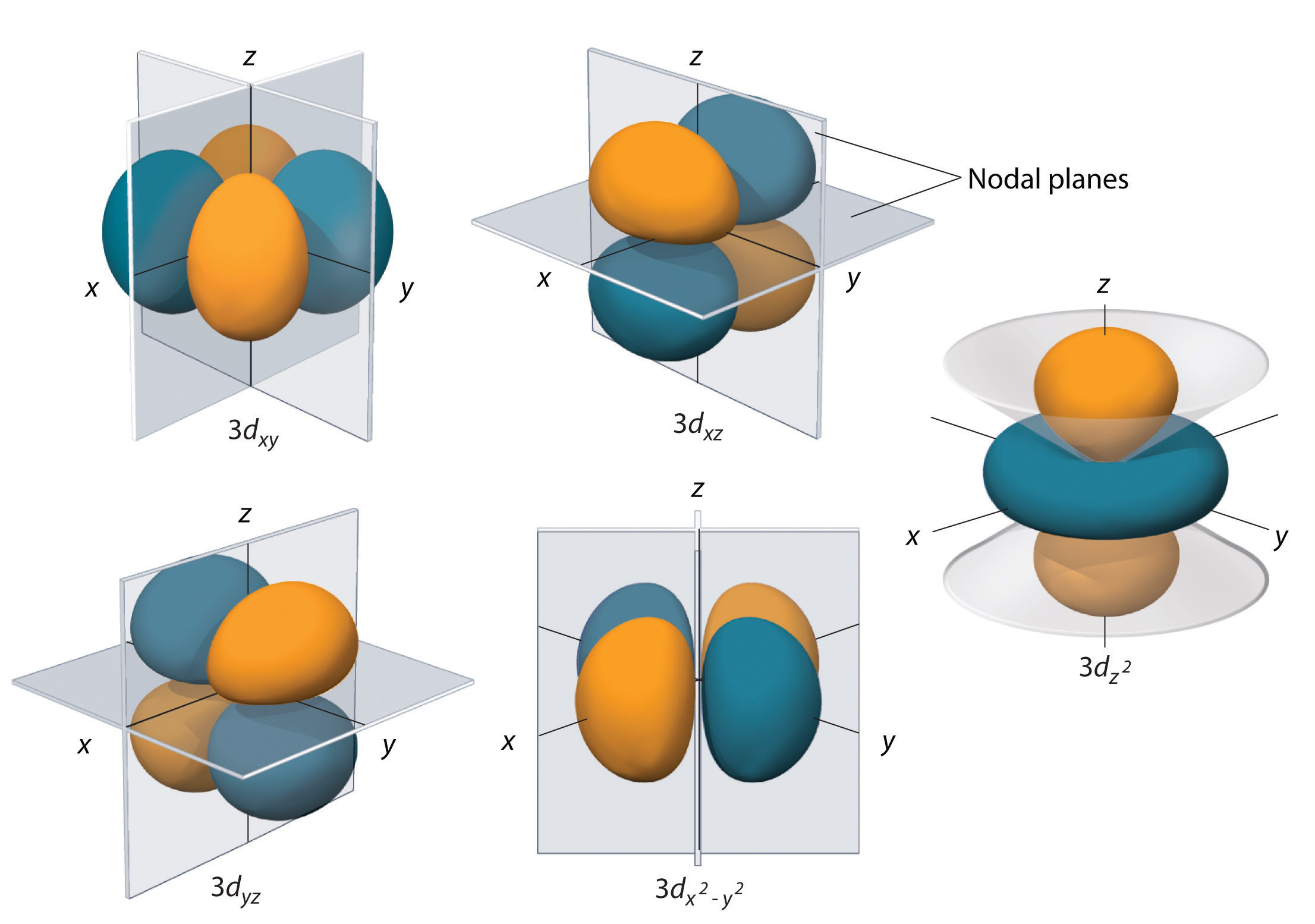
De waterstof 3d orbitalen, weergegeven in figuur figuur \(3d_{z^2}), hebben een complexere vorm dan de 2p orbitalen. Alle vijf 3d banen bevatten twee nodale oppervlakken, vergeleken met één voor elke p orbitaal en nul voor elke s orbitaal. In drie van de d-banen zijn de lobben van de elektronendichtheid georiënteerd tussen het x- en y-vlak, x- en z-vlak, en y- en z-vlak; deze orbitalen worden respectievelijk de 3d-banen, 3dxz-banen en 3d-z-banen genoemd. Een vierde d orbitaal heeft lobben die langs de x- en y-as liggen; dit is de 3d orbitaal. De vijfde 3d orbitaal, die de (3d_{z^2}) orbitaal wordt genoemd, heeft een unieke vorm: hij lijkt op een (2p_z) orbitaal gecombineerd met een extra donut van elektronwaarschijnlijkheid die in het xy-vlak ligt. Ondanks zijn eigenaardige vorm is de 3d-baan wiskundig gelijkwaardig aan de andere en heeft dezelfde energie. In tegenstelling tot p-banen is de fase van de golffunctie voor d-banen dezelfde voor tegengestelde lobbenparen. Zoals te zien in figuur is de fase van de golffunctie positief voor de twee lobben van de d-baan die langs de z-as liggen, terwijl de fase van de golffunctie negatief is voor de donut van elektronendichtheid in het xy-vlak. Net als bij de s- en p-banen neemt bij toenemende n de grootte van de d-banen toe, maar de globale vorm blijft gelijk aan die van figuur 5.
f-banen (l=3)
Principale schillen met n = 4 kunnen subschillen hebben met l = 3 en ml-waarden van -3, -2, -1, 0, +1, +2, en +3. Deze subschillen bestaan uit zeven f-orbitalen. Elke f orbitaal heeft drie knooppuntoppervlakken, zodat de f-vormen complex zijn. Omdat f-banen niet zo belangrijk zijn voor ons doel, bespreken we ze niet verder, en orbitalen met hoge l-waarden bespreken we helemaal niet.
Orbitale energieën
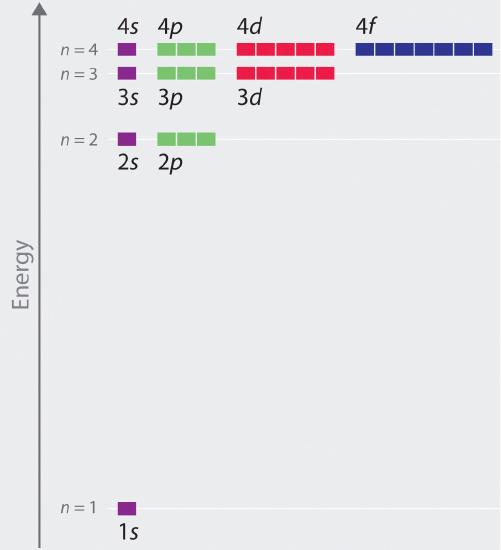
Hoewel we de vormen van orbitalen besproken hebben, hebben we weinig gezegd over de i(r)-vergelijkende energieën. We beginnen de bespreking van de baanenergieën door atomen of ionen met slechts een enkel elektron (zoals H of He+) te beschouwen. De relatieve energieën van de atoombanen met n ≤ 4 voor een waterstofatoom zijn uitgezet in figuur 6. Merk op dat de baanenergieën alleen afhangen van het hoofdkwantumgetal n. Bijgevolg zijn de energieën van de 2s en 2p banen van waterstof dezelfde; de energieën van de 3s, 3p, en 3d banen zijn dezelfde; enzovoort. De kwantummechanica voorspelt dat in het waterstofatoom alle orbitalen met dezelfde waarde van n (b.v. de drie 2p-banen) ontaard zijn, hetgeen betekent dat zij dezelfde energie hebben. De banenergieën die met behulp van de kwantummechanica voor waterstof zijn verkregen, zijn precies gelijk aan de toegestane energieën die Bohr heeft berekend. Maar in tegenstelling tot het model van Bohr, dat slechts één baan per energieniveau toestond, voorspelt de kwantummechanica dat er 4 banen met verschillende elektronendichtheidsverdelingen zijn in de n = 2 hoofdschil (één 2s en drie 2p banen), 9 in de n = 3 hoofdschil, en 16 in de n = 4 hoofdschil.De verschillende waarden van l en ml voor de afzonderlijke orbitalen binnen een bepaalde hoofdschil zijn niet van belang voor het begrijpen van de emissie- of absorptiespectra van het waterstofatoom onder de meeste omstandigheden, maar zij verklaren wel de splitsingen van de hoofdlijnen die worden waargenomen wanneer waterstofatomen in een magnetisch veld worden geplaatst. Figuur 26 laat zien dat de energieniveaus dicht bij elkaar komen te liggen naarmate de waarde van n toeneemt, zoals verwacht vanwege de 1/n2-afhankelijkheid van de baanenergie.
De energieën van de banen in elke soort met slechts één elektron kunnen worden berekend met een minovariant van de vergelijking van Bohr, die kan worden uitgebreid tot andere soorten met één elektron door de lading van de atoomkern (het aantal protonen in de kern) erbij te betrekken:
In het algemeen nemen zowel de energie als de straal af naarmate de nuclea(r)-lading toeneemt. De meest stabiele banen (die met de laagste energie) zijn dus die welke het dichtst bij de kern liggen. Bijvoorbeeld, in de grondtoestand van het waterstofatoom bevindt het enkele elektron zich in de 1s orbitaal, terwijl in de eerste aangeslagen toestand het atoom energie heeft geabsorbeerd en het elektron is gepromoveerd naar een van de n = 2 orbitalen. In ionen met slechts een enkel elektron hangt de energie van een bepaalde orbitaal alleen af van n, en alle subschillen binnen een hoofdschil, zoals de n(p_x), n(p_y), en n(p_z) orbitalen, zijn degeneraat.
Samenvatting
De chemisch belangrijke typen atoombanen corresponderen met waarden van \ell = 0, \1, \2, en \3. Banen met een waarde van 0 zijn s-banen en zijn bolvormig symmetrisch, waarbij de kans dat het elektron in de kern zit het grootst is. Alle banen met waarden (n > 1) en ell = 0 bevatten één of meer knopen. Orbitalen met ell = 1 zijn p-banen en bevatten een knooppuntvlak dat de kern omvat, waardoor een haltervorm ontstaat. Orbitalen met d(ell = 2) zijn d-banen en hebben een complexere vorm met tenminste twee knooppuntvlakken. Banen met f(ell = 3) zijn f-banen, die nog complexer zijn.
Omdat de gemiddelde afstand tot de atoomkern de energie van een elektron bepaalt, is aan elke atoombaan met een gegeven reeks kwantumgetallen een bepaalde energie verbonden, de orbitalenergie.
In atomen o(r)ionen met slechts een enkel elektron hebben alle banen met dezelfde waarde van \(n) dezelfde energie (zij zijn gedegenereerd), en de energieën van de hoofdschilden nemen gelijkmatig toe naarmate \(n) toeneemt. Een atoomion met de elektron(en) in de onderste energieruimte(n) bevindt zich in de grondtoestand, terwijl een atoomion met één of meer elektronen in hogere energiebanen zich in een aangeslagen toestand bevindt.
Bijdragers en toeschrijvingen
-
Gewijzigd door Joshua Halpern (Howard University)